FexCy micro-mechanical properties based on response surface methodology and molecular dynamics
-
摘要: 探究了不同碳钢材料在不同温度下的力学性能响应状况，采用分子动力学建立仿真模型，通过三因素多水平正交试验和响应面法建立回归模型，研究C含量、空位比以及温度对杨氏模量E和屈服强度Q的影响。在相同的C含量和空位比条件下，利用Matlab的随机函数建立了50个模型，每种试验条件进行50次仿真。统计杨氏模量和屈服极限的中位数作为反应材料力学性能的关键参数，建立响应面回归模型。通过随机选取10组仿真试验验证，成功地探究了不同因素对碳钢力学性能的影响规律，得到了材料力学参数的可靠数学模型，并对材料成分组成进行了优化设计。Abstract: This research is to investigate the mechanical properties of different carbon steel materials at different temperatures. The simulation model was established by using molecular dynamics, and the regression model was established by the three-factor multi-level orthogonal test and response surface method to study the effects of C content, vacancy ratio and temperature on Young’s modulus and yield strength. Under the same C content and vacancy ratio conditions, 50 models were established by using the random function of Matlab, and each test condition was simulated 50 times. The median of Young’s modulus and yield limit were used as key parameters of the mechanical properties of the reaction materials, and the response surface regression model was established. By randomly selecting 10 groups of simulation experiments, this study successfully explored the influence of different factors on the mechanical properties of carbon steels, obtaining a reliable mathematical model of materials mechanical parameters, and optimizing the composition of materials.
-
Key words:
- molecular dynamics /
- response surface analysis /
- Young’s modulus /
- yield strength
-
0. 引言
低碳钢被广泛地应用于航天发射架、冶金机械、核产业、内燃机等工作环境处于高温环境中的机械结构中。C含量、制造过程中产生的空位比在不同的温度下会有不同的力学性能。因此需要研究温度对低碳钢力学性能的影响。传统方法通过材料试制再进行试验的方法会造成大量人力物力的浪费，而分子动力学可以通过仿真计算节约成本，缩短材料研发时间，从而为学者们预测材料的力学性能提供了一种新的方法。李翔[1]利用分子动力学研究了α-Fe塑性变形行为；韦昭召[2]通过分子动力学探究了Fe合金马氏体相变晶体学特征；袁玉全[3]用分子动力学模拟了Fe拉伸与疲劳裂纹扩展，对其机理进行了一定的研究；王云天[4]的研究表明温度升高单晶铁的成核阈值会随之降低。同时，研究表明空位率与C含量[5]会影响低碳钢的力学性能。
传统的多因素多水平试验会造成试验次数多，试验难度大的问题。为减少试验次数可以利用正交试验设计，加快试验进展。此前，响应面法多用于化学、医药、生物以及机械设计等领域，近年来开始应用于材料的力学性能预测研究。曲晨驰[6]为改善Al-Cu-Sc合金的导电性以及力学性能，利用响应面法优化了材料的Cu、Sc含量；胡静[7]建立了ECC基体的二次多项式回归模型并且对材料配比进行了优化。响应面法对多因素影响分析具有较好的拟合效果。
因此，笔者首先对三种因素多水平试验利用响应面法进行试验设计，再利用Matlab建立多个随机模型，利用分子动力学研究Fe-C合金C含量、空位比、温度对杨氏模量、屈服极限的影响并进行统计，利用响应面法建立三因素双目标的数学模型。然后随机选取10组组合条件对所建立的数学模型进行验证，对影响低碳钢材料力学性能的因素进行了探究。最后通过所建立的数学模型对材料配比进行了优化。
1. 仿真模型与模拟试验方法
1.1 仿真模型设置
采用分子动力学方法对FeC合金在原子尺度下进行单轴拉伸仿真，FeC体系采用开源大规模原子/分子并行模拟器LAMMPS，模拟时首先进行了能量最小化，然后在NPT体系内进行了10 ps的弛豫，最后在微正则体系NVE体系下进行拉伸，采用速度标定法进行控温。初始模型的尺寸为$ 18.6186\text{ nm}\times18.6186\text{ nm}\times1.1457\; 6\ \text{nm} $，共有34 000个原子，Fe原子晶胞排布方式为BCC，C原子与空位随机分布在Fe基中。通过改变盒子Y方向上的尺寸，以恒定的应变率$ \mathrm{\varepsilon}_{\mathrm{y}\mathrm{y}}=10^{10\ }\mathrm{s}^{-1} $进行Y轴拉伸，Y方向的应变可以用公式（1）表示为。
$$ {\varepsilon }_{yy}=\frac{{l}_{y}-{l}_{y0}}{{l}_{y0}} $$ (1) 仿真时间步设置为0.001 ps，三个方向均设置为周期边界，仿真步数为30 000。利用Windows批量化处理程序“*.dat”脚本实现批量化仿真，通过Ovito进行可视化处理，对应力-应变数据采用lammps自带的数据输出“fix print”函数，再使用Matlab进行批量化处理。
HEPBURN[8]对Fe-C原子间相互作用进行了研究，经过Sebastien Garruchet的修改得到了Fe-C嵌入原子势（EAM）来描述Fe-C合金内部的原子间相互作用力。文中研究是基于其提出的eam.fs原子势函数进行的。
1.2 模拟试验方法
响应面法的基本思想是基于数学回归思想，通过对设计空间中不同点的拟合，用回归模型代替复杂模型。研究采用Design-Expert中的optimal设计方法进行更为灵活的试验设计。低碳钢的含碳量（C原子数）大约在1%～2.2%，空位率大约在1%～5%，低碳钢力学性能温度范围设定为300～900 K，根据叶天舟[9]研究，低合金钢在超过900 K温度后力学性能迅速劣化，不适宜再作为主要的支撑材料。所有因素的水平分级均采用均匀化设置，温度水平设置为4水平，C含量与空位比水平设置为5。因素水平设计以及对应的数值如表1所示。
表 1 因素水平设计Table 1. Design of factors and levels水平等级 影响因素 温度T/K 含C量R/% 空位比V/% −2 300 1 1 −1 500 1.3 2 0 700 1.6 3 1 900 1.9 4 2 2.2 5 根据表2中20组试验情况进行仿真，因微观力学性能与局部原子、空位分布也有关系，因此为减少这种随机关系对材料力学参数统计的影响，每种情况进行50次仿真，取各自杨氏弹性模量E以及屈服强度Q(后文均以E指代杨氏弹性模量、Q指代屈服强度）的中位数作为该情况下的材料参数。
表 2 响应面试验设计Table 2. Experimental design of response surface method编号 温度T/K 含C量R/% 空位比V/% 编号 温度T/K 含C量C/% 空位比V/% 1 500 1 3 11 300 1.6 2 2 900 1 2 12 700 1.3 2 3 900 1.6 3 13 900 2.2 5 4 500 1 3 14 900 1.6 1 5 500 1.6 5 15 300 1 5 6 500 1.6 5 16 900 1.6 3 7 700 2.2 1 17 900 1 5 8 300 2.2 2 18 300 2.2 4 9 900 2.2 3 19 700 1.3 2 10 700 2.2 1 20 300 1.6 2 2. 仿真结果与分析
2.1 分子动力学仿真分析
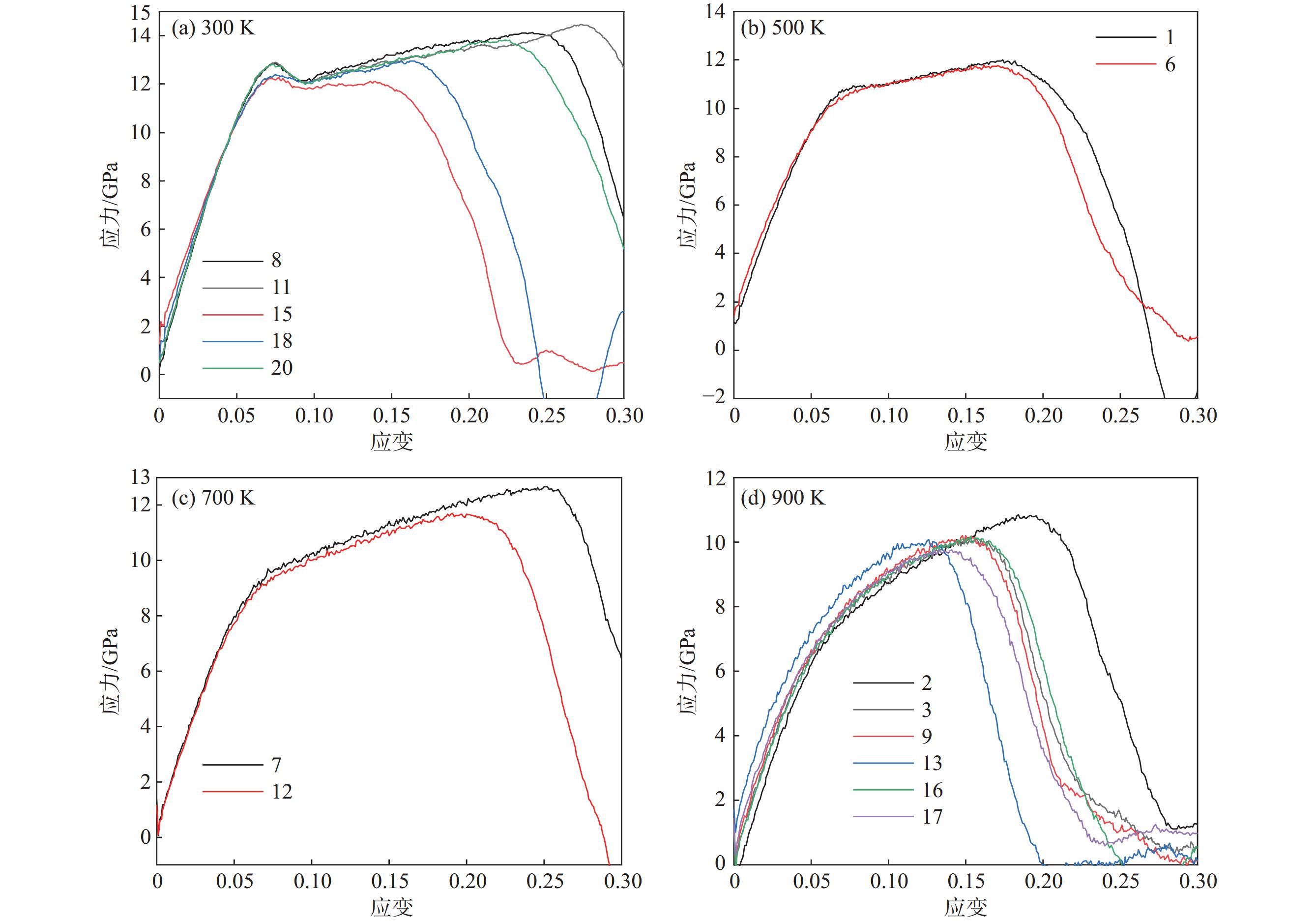
以300 K1R1V(300 K：300 K的温度，1R：含碳量1%，1V：空位比1%)的单轴拉伸模型为例，如图1所示，对拉伸过程中晶胞类型进行分析。可以发现单轴拉伸时晶粒产生明显的位错，从10 ps到20 ps变化显著，直至30 ps时由于原子间距过大，已经很难保持BCC晶胞结构，几乎完全被其他（非典型晶胞结构）替代。
从300～700 K低碳钢微观拉伸过程中，材料有明显的线弹性阶段。在300 K中，经过线弹性阶段后有明显的应变软化过程，之后再发生塑性断裂；同时随着温度的升高，应变软化效应逐渐消失，在高温900 K下低碳钢不再具有明显的线弹性阶段，并且随着温度的升高材料的屈服应力有下降的趋势，应力应变如图2所示。
按照1.2中提及的参数取值方法，将分子动力学性能结果统计至表3中。
表 3 分子动力学性能平均值Table 3. Average molecular dynamics properties编号 E/GPa Q/GPa 编号 E/GPa Q/GPa 1 152.616 10.9617 11 205.276 12.8755 2 42.6706 9.9332 12 90.412 10.0607 3 56.319 9.4425 13 88.4735 9.7228 4 152.616 10.9617 14 36.4433 9.7911 5 168.574 10.8488 15 205.762 12.2664 6 168.574 10.8488 16 56.319 9.4425 7 86.3013 10.0222 17 81.2357 9.5083 8 213.773 12.8354 18 220.891 12.4089 9 58.739 9.4343 19 90.412 10.0607 10 86.3013 10.0222 20 205.276 12.8755 2.2 响应面模型建立
利用Design-Expert软件对E、Q建立温度T、含碳量R以及空位比V三变量之间的多种拟合模型分析，分别对linear、2FI、square、cubic进行显著性分析，通过对模型显著性检测、失拟项检测和相关性检测的数据进行对比，选择最优的模型进行试验数据分析，结果如表4所示。
表 4 杨氏模量和屈服强度多种模型综合分析结果Table 4. Results of comprehensive analysis of Young’s modulus and yield strength models模型 $ P $ $ {R}^{2} $ 顺序P值 校正值 预测值 E 线性 < 0.0001 0.9868 0.9799 两因素 < 0.0001 0.9975 0.9956 平方 0.0471 0.9985 0.9936 三次 1.0000 Q 线性 < 0.0001 0.9887 0.8635 两因素 0.2947 0.9053 0.7766 平方 < 0.0001 0.9970 0.9847 三次 1.0000 一般认为$ P < 0.01 $为非常显著，$ 0.01 \leqslant P \leqslant 0.05 $为显著，$ P > 0.05 $为不显著。由表4可知，弹性模量模型中两因素多项式和平方多项式的$ {R}^{2} $均在0.99以上，线性多项式和两因素多项式为极显著，综合判断E值拟合使用两因素多项式模型；屈服强度的线性多项式和平方多项式为显著，同时平方多项式$ {R}^{2} $校正值在所有模型中最大，为
0.9970 ，$ {R}^{2} $预测值为0.9847， 接近1，因此选择平方多项式模型作为屈服强度回归模型。根据表3对E、Q建立温度T、含碳量R以及空位比V三变量的响应面回归模型，见式(2)、(3)。$$ \begin{split} &\qquad E(T,R,V) = 266.110\;93 - 0.274\;192T + 14.144\;9R\\ & -4.381\;64V-0.018\;139TR+0.017\;048TV\\ & +1.618\;67RV \end{split} $$ (2) $$ \begin{split} & \qquad Q\left(T,R,V\right) = 19.078\;29 - 0.015\;987T - 0.861\;465R\\ & -0.969\;765V- 0.000\;179TR+0.000\;285TV\\ & +0.172\;086RV+8.504\;25\times {10}^{-6}{T}^{2}+0.098\;446{R}^{2}\\ & +0.064\;218{V}^{2} \end{split} $$ (3) 为了验证式（2）（3）的可靠性，对其进行方差以及可信度检验分析，杨氏模量回归模型方差的分析结果如表5所示，屈服极限回归模型方差分析结果如表6所示。
表 5 杨氏模量回归模型方差分析Table 5. Variance analysis of Young’s modulus of compressive strength regression model平方和 自由度 均方值 F值 P值 是否显著 $ E\left(T,R,V\right) $ 78703.48 6 13117.25 1275.1 < 0.0001 显著 $ T $ 68447.57 1 68447.57 6653.63 < 0.0001 显著 $ R $ 246.39 1 246.39 23.95 0.0003 显著 $ V $ 2374.5 1 2374.5 230.82 < 0.0001 显著 $ TR $ 73.67 1 73.67 7.16 0.019 显著 $ TV $ 535.98 1 535.98 52.1 < 0.0001 显著 $ RV $ 20.23 1 20.23 1.97 0.1843 残差 133.73 13 10.29 总变异值 78837.22 19 表 6 屈服极限回归模型方差分析Table 6. Variance analysis of yield limit of compressive strength regression model平方和 自由度 均方值 F值 P值 是否显著 $ Q\left(T,R,V\right) $ 29.82 9 3.31 709.77 < 0.0001 显著 $ T $ 26.93 1 26.93 5769.72 < 0.0001 显著 $ R $ 0.0588 1 0.0588 12.61 0.0053 显著 $ V $ 0.4652 1 0.4652 99.65 < 0.0001 显著 $ TR $ 0.0069 1 0.0069 1.47 0.2534 $ TV $ 0.1378 1 0.1378 29.51 0.0003 显著 $ RV $ 0.1589 1 0.1589 34.03 0.0002 显著 $ {T}^{2} $ 1.87 1 1.87 401.02 < 0.0001 显著 $ {R}^{2} $ 0.005 1 0.005 1.08 0.3234 $ {V}^{2} $ 0.1421 1 0.1421 30.43 0.0003 显著 残差 0.0467 10 0.0047 总变异值 29.87 19 模型$ E\left(T,R,V\right) $与$ Q\left(T,R,V\right) $的P值均小于
0.0001 ，说明两个模型建立极显著。$ E\left(T,R,V\right) $的F值为1275.1 ，$ Q\left(T,R,V\right) $的F值为709.77，模型只有0.01%的可能性是由于噪音产生的结果。大部分因素对模型的影响因素较为显著，因此模型建立良好。从方差分析可以得出$ T $、$ R $、$ V $对杨氏模量以及屈服强度的影响均为显著，含碳量$ R $相较于另两个变量显著性较差。两因素的交互影响对杨氏模量的影响：温度与含碳量以及温度与空位率影响较为显著，而含碳量与空位率的影响并不显著。两因素交互影响对屈服极限的影响：温度与空位率以及空位率与含碳量的影响为显著；温度与含碳量的影响并不显著，模型可信度检验分析如表7所示。表 7 模型可信度检验分析Table 7. Reliability test and analysis of the model模型 标准差 相关系数 调整系数 变异系数/% 信噪比 $ E\left(T,R,V\right) $ 3.21 0.9983 0.9975 2.6 100.5393 $ Q\left(T,R,V\right) $ 0.0683 0.9984 0.9970 0.6376 72.3359 根据模型的可信度检验分析可知，相关系数分别为
0.9983 、0.9970 ；调整系数分别为0.9975 、0.9970 ；信噪比分别为100.5393 、72.3359， 远大于4，说明回归模型可靠性较高。2.3 响应面分析
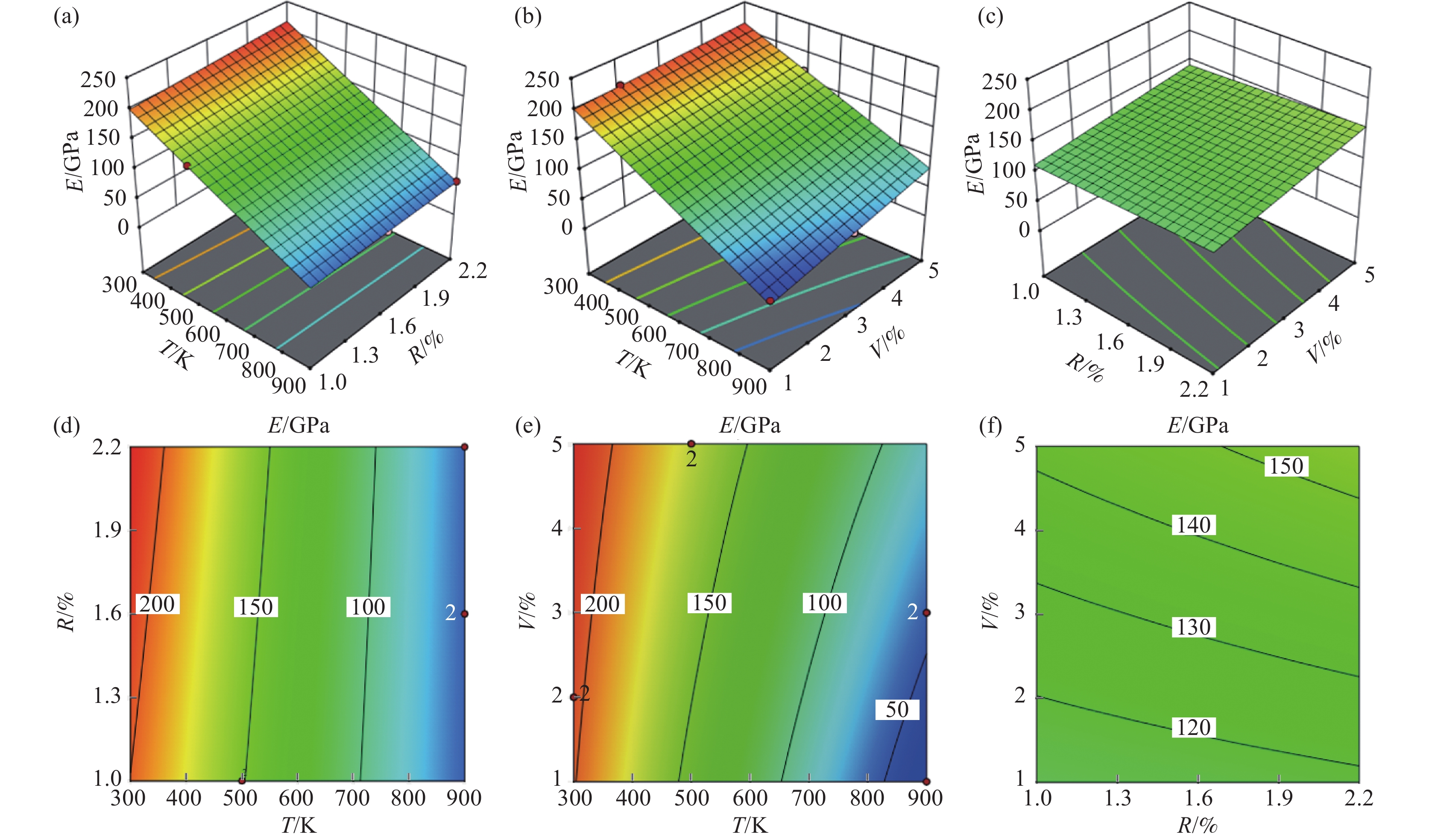
由图3可以看出，杨氏模量随着温度的升高而逐渐降低，降低的速度逐渐变快。杨氏模量随着空位率的增大而逐渐变大，这是由于空位率造成了低碳钢晶体内部位错的产生，而位错阻止了拉伸。随着含碳量的增大，杨氏模量逐渐变大，但是变化趋势并不明显，含碳量对低碳钢的杨氏模量影响并不显著。
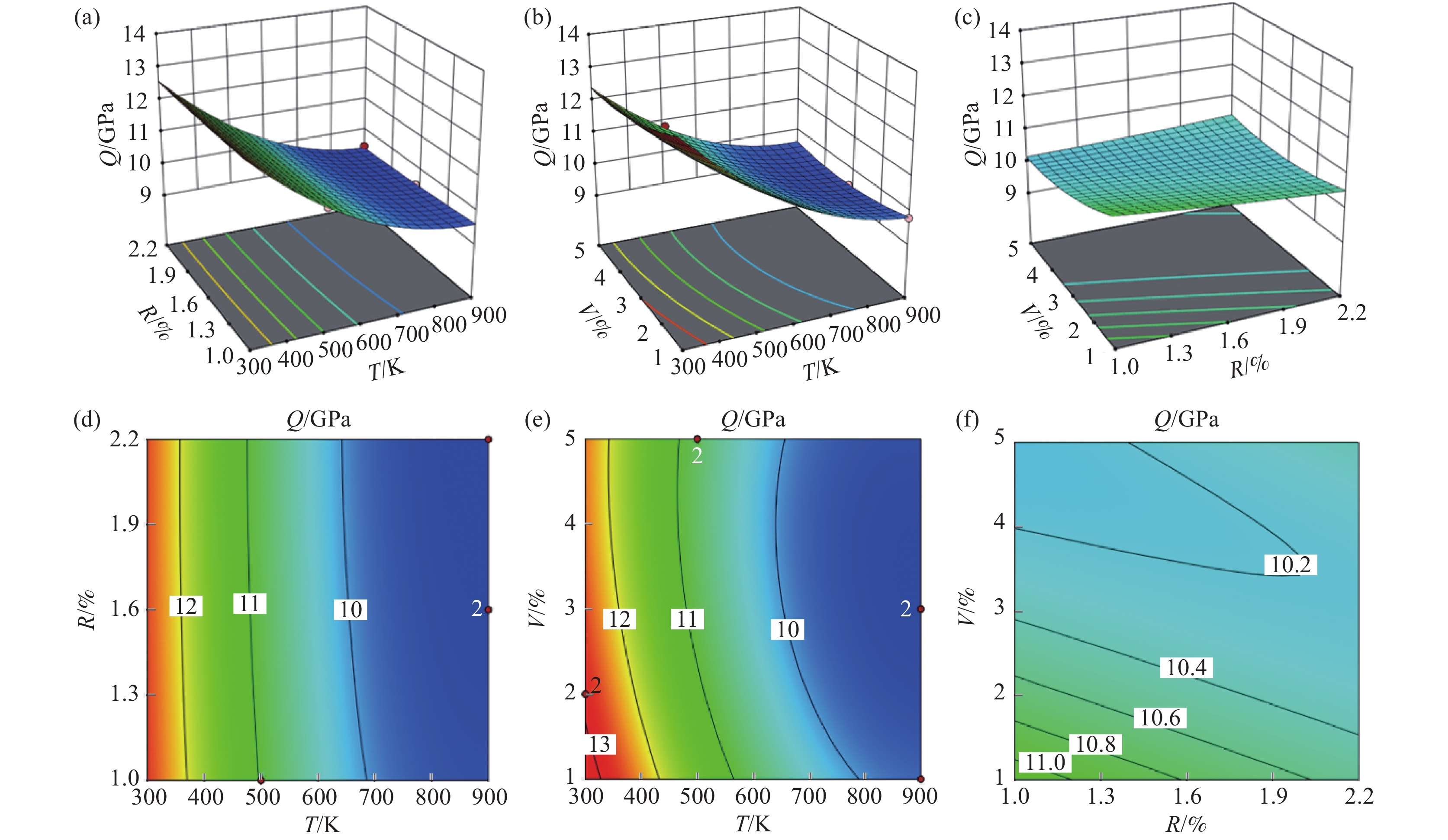
图 3 杨氏模量响应曲面及等高线图(a)(d)温度、含碳量与杨氏模量的关系；(b)(e)温度、空位比与杨氏模量的关系；(c)(f)含碳量、空位比与杨氏模量的关系Figure 3. Young's modulus response surfaces and contour maps从图4可以得出，屈服强度随着温度的升高而逐渐降低，变化速度逐渐减慢。随着空位率的增加，由于局部缺陷的增加，屈服强度逐渐减小，这种减小的趋势同样是逐渐变缓。含碳量的增加使得屈服强度减小，碳含量的增加使得单晶碳钢更易进入屈服阶段。
图 4 屈服强度响应曲面及等高线(a)(d)温度、含碳量和屈服强度的关系；(b)(e)温度、空位比与屈服强度的关系；(c)(f)含碳量、空位比与屈服强度的关系Figure 4. Yield strength response surfaces and contours3. 模型验证及优化
3.1 模型验证
为了对第2-2节得到的响应面模型进行验证，证明模型的可行性，现对变量梯度范围内进行随机组合。另组合十组仿真试验，每次试验条件同样进行50次仿真，按照与上述内容相同的方式对杨氏模量以及屈服强度进行计算。因正交试验未对C含量为1.9%的条件进行，因此选取5组C含量为1.9%的试验，另5组随机选取。选取的条件以及结果见表8。
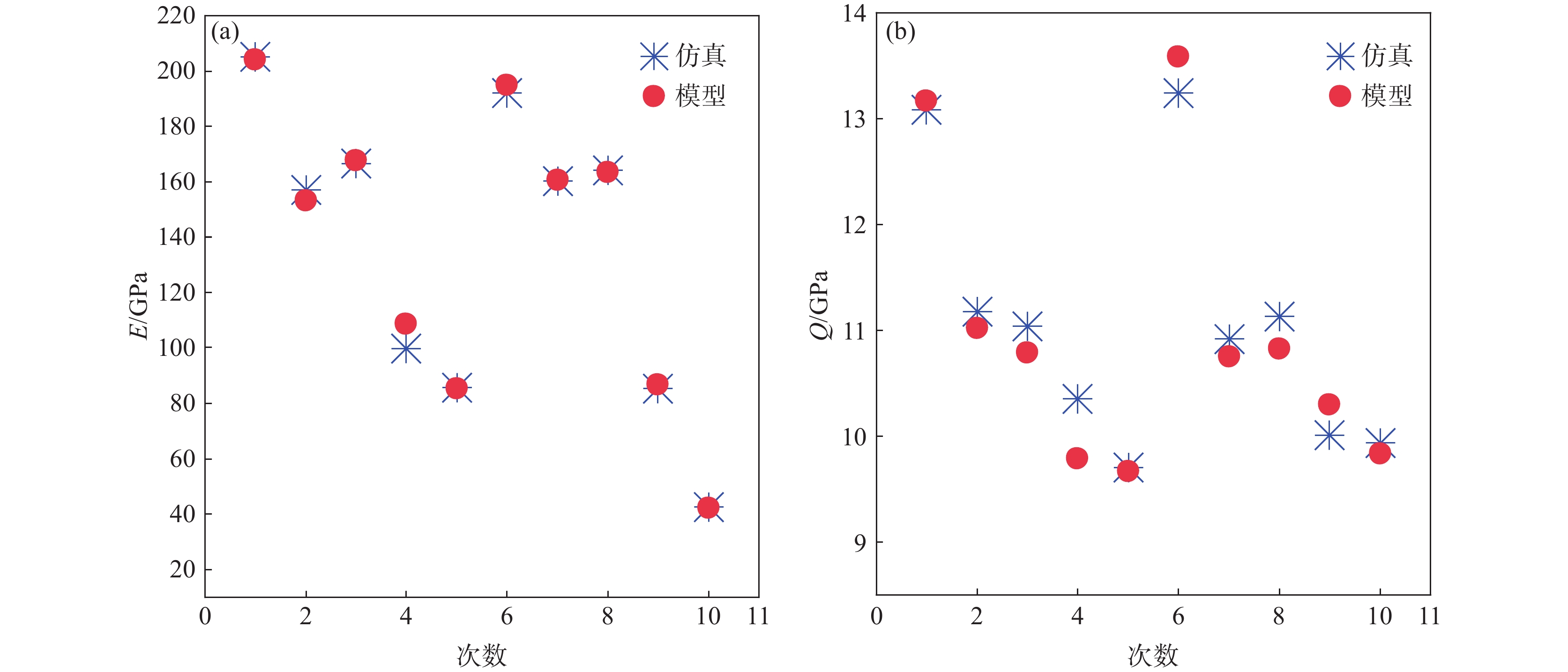
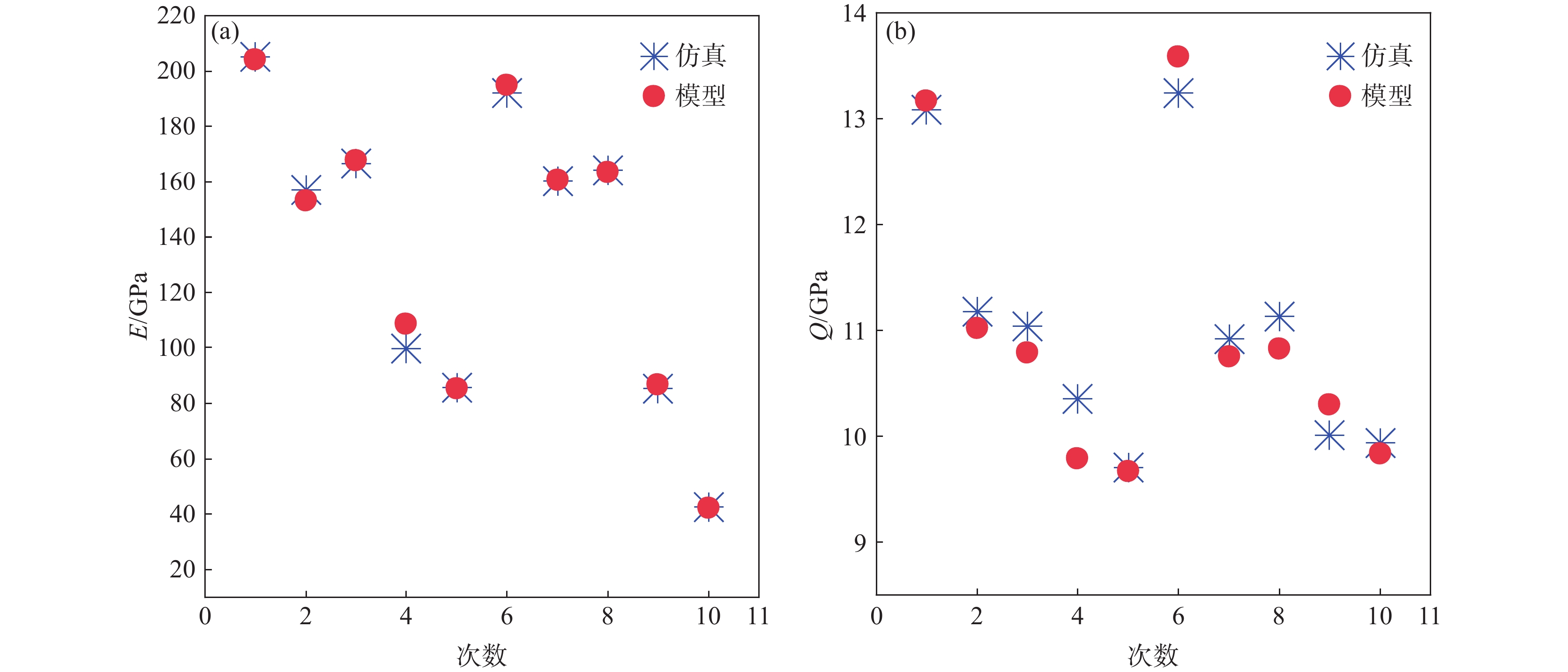
表 8 验证不同温度T、含碳量R以及空位率V下的仿真试验结果Table 8. Verification of the simulation results under different temperatures T, carbon contents R and vacancy rates V编号 组合 $ E $/GPa $ Q $/GPa 温度T/K 含碳量R/% 空位率V/% 1 300 1.9 1 205.1847 13.0851 2 500 1.9 2 156.9726 11.1803 3 500 1.9 4 166.5242 11.0399 4 700 1.9 3 99.7662 10.3489 5 900 1.9 5 85.7702 9.7070 6 300 1 1 192.1814 13.2412 7 500 1.3 4 160.2058 10.9185 8 500 2.2 3 164.0080 11.1295 9 700 1.6 1 85.3685 10.0065 10 900 1 2 42.6706 9.9332 根据式（2）（3）分别计算得与表7对应情况下的模型预测值，将预测值与仿真试验值绘制到图5中。图5(a)表示弹性模量的模型预测值与仿真值，图5(b)表示屈服强度的预测值与仿真值。
从图5可以看出，弹性模量E和屈服强度Q的模型预测值与仿真值大部分十分接近，只有温度为700 K、含碳量为1.9%、空位率3%的情况下，仿真值与模型计算结果出入较大。由图5可以看出，弹性模量的预测结果有9个值，几乎完全重合，屈服强度的预测值与仿真值结果大部分也较为吻合。为更好地统计误差，对仿真得到的数值与模型预测的数值进行误差分析，其结果记录在表9中。
表 9 仿真值与预测值误差Table 9. The errors of simulation and prediction values编号 $ E $ $ Q $ 绝对误差/GPa 相对误差/% 绝对误差/GPa 相对误差/% 1 0.99 0.48 0.09 0.66 2 3.88 2.47 0.16 1.47 3 1.01 0.60 0.25 2.30 4 9.04 9.06 0.57 5.46 5 0.39 0.45 0.04 0.43 6 2.73 1.42 0.34 2.58 7 0.39 0.24 0.16 1.50 8 0.72 0.44 0.30 2.72 9 1.27 1.48 0.29 2.90 10 0.35 0.83 0.10 1.05 由表9可知，除第4次仿真结果与预测值杨氏模量相差较大外，最大的相对误差为9.06%，大部分相对误差保持在5%以内；屈服强度最大的相对误差为5.46%，其余相对误差在5%以内。预测值与仿真值满足工程误差范围，验证了模型对于工程应用的有效性，与常温Q235钢相比较[10]，由于其仿真建模忽略了晶界影响，弹性模量略低，屈服强度远高于宏观材料。
3.2 元素组成响应面优化
采用Design-Expert对低碳钢中元素比进行优化，低碳钢作为承载部件的主要材料，需要有足够的强度和抵抗变形的能力。在复杂载荷环境中，尤其是高温载荷下，材料的力学性能可能会出现迅速劣化。因此对低碳钢的元素组成进行优化时，优化标准是在高温下获得高屈服强度和高弹性模量。
根据上述优化条件，最终Design-Expert的优化结果是，在高温载荷750、800、850、900 K下，含碳量$ R $、空位率$ V $分别为2.2、5。而高空位率在常温情况下力学性能极差，因此应在优化目标中添加空位率取值范围规定为1%～2%，并将预测结果与仿真结果记录在表10中。
表 10 优化结果预测值与仿真值Table 10. Optimized results of the predicted values and simulation valuesT/K R/% V/% $ E $ $ Q $ 预测
/GPa仿真
/GPa相对
误差/%预测
/GPa仿真
/GPa相对
误差/%750 1.018 1.004 71.108 70.349 1.067 10.442 10.220 2.126 800 1.004 1.120 58.572 59.145 0.978 10.266 10.153 1.101 850 1.063 1.499 49.431 50.017 1.185 9.996 10.092 0.960 900 1.000 2.000 42.317 42.671 0.837 9.829 9.933 1.058 所建立的杨氏模量模型预测值和仿真值最大误差为1.185%，所建立的屈服强度模量模型预测值和仿真值最大误差为2.126%，满足工程需求。为确保常温至高温载荷下均具有较好的力学性能，含碳量不应超过1.1%，随着温度载荷的升高，优化结果空位率增高。
4. 结论
采用响应面法对仿真试验组合进行了设计，依据仿真数据建立了温度T、含碳量R、空位率V与碳钢弹性模量E、屈服强度Q之间的响应面回归模型。根据模型分析，得出温度T、含碳量R、空位率V对单晶碳钢的力学性能显著。
1)随着温度T升高，由于原子越来越活跃，原子间开始出现相互远离的趋势，弹性模量E、屈服强度Q减小。随着含碳量R的增加，碳钢弹性模量增大，屈服强度减小，单晶碳钢韧性变差。由于空位率V的增加导致晶体内部位错增加，当晶体拉伸时，位错阻止晶体变形，因此弹性模量增大，而由于局部缺陷增加，使得屈服强度降低，单晶碳钢刚度增加。
2)随机组成10组仿真模型对所提数学模型进行验证，模型拟合程度较高。根据模型进一步优化材料元素组成，得到的预测值与仿真试验值之间最大误差小于5%。当材料处于900 K载荷，时空位率为2%、含碳量为1%的单晶碳钢力学性能最佳。不同温度载荷下所得到的最佳力学性能材料配比有所不同，适当提高C含量和空位率可以改善高温情况下的材料力学性能。
3)研究结果可以用于预测不同碳钢材料在不同条件下的力学性能，为材料选择和设计提供指导。在特定的工程应用中，可以根据所需的力学性能要求选择合适的碳钢材料或确定最佳的使用条件，这将有助于更准确地预测和优化材料的力学性能，为工程设计和材料科学研究提供有力工具。
-
图 3 杨氏模量响应曲面及等高线图
(a)(d)温度、含碳量与杨氏模量的关系；(b)(e)温度、空位比与杨氏模量的关系；(c)(f)含碳量、空位比与杨氏模量的关系
Figure 3. Young's modulus response surfaces and contour maps
图 4 屈服强度响应曲面及等高线
(a)(d)温度、含碳量和屈服强度的关系；(b)(e)温度、空位比与屈服强度的关系；(c)(f)含碳量、空位比与屈服强度的关系
Figure 4. Yield strength response surfaces and contours
表 1 因素水平设计
Table 1. Design of factors and levels
水平等级 影响因素 温度T/K 含C量R/% 空位比V/% −2 300 1 1 −1 500 1.3 2 0 700 1.6 3 1 900 1.9 4 2 2.2 5 
下载: 导出CSV
表 2 响应面试验设计
Table 2. Experimental design of response surface method
编号 温度T/K 含C量R/% 空位比V/% 编号 温度T/K 含C量C/% 空位比V/% 1 500 1 3 11 300 1.6 2 2 900 1 2 12 700 1.3 2 3 900 1.6 3 13 900 2.2 5 4 500 1 3 14 900 1.6 1 5 500 1.6 5 15 300 1 5 6 500 1.6 5 16 900 1.6 3 7 700 2.2 1 17 900 1 5 8 300 2.2 2 18 300 2.2 4 9 900 2.2 3 19 700 1.3 2 10 700 2.2 1 20 300 1.6 2
下载: 导出CSV
表 3 分子动力学性能平均值
Table 3. Average molecular dynamics properties
编号 E/GPa Q/GPa 编号 E/GPa Q/GPa 1 152.616 10.9617 11 205.276 12.8755 2 42.6706 9.9332 12 90.412 10.0607 3 56.319 9.4425 13 88.4735 9.7228 4 152.616 10.9617 14 36.4433 9.7911 5 168.574 10.8488 15 205.762 12.2664 6 168.574 10.8488 16 56.319 9.4425 7 86.3013 10.0222 17 81.2357 9.5083 8 213.773 12.8354 18 220.891 12.4089 9 58.739 9.4343 19 90.412 10.0607 10 86.3013 10.0222 20 205.276 12.8755
下载: 导出CSV
表 4 杨氏模量和屈服强度多种模型综合分析结果
Table 4. Results of comprehensive analysis of Young’s modulus and yield strength models
模型 $ P $ $ {R}^{2} $ 顺序P值 校正值 预测值 E 线性 < 0.0001 0.9868 0.9799 两因素 < 0.0001 0.9975 0.9956 平方 0.0471 0.9985 0.9936 三次 1.0000 Q 线性 < 0.0001 0.9887 0.8635 两因素 0.2947 0.9053 0.7766 平方 < 0.0001 0.9970 0.9847 三次 1.0000
下载: 导出CSV
表 5 杨氏模量回归模型方差分析
Table 5. Variance analysis of Young’s modulus of compressive strength regression model
平方和 自由度 均方值 F值 P值 是否显著 $ E\left(T,R,V\right) $ 78703.48 6 13117.25 1275.1 < 0.0001 显著 $ T $ 68447.57 1 68447.57 6653.63 < 0.0001 显著 $ R $ 246.39 1 246.39 23.95 0.0003 显著 $ V $ 2374.5 1 2374.5 230.82 < 0.0001 显著 $ TR $ 73.67 1 73.67 7.16 0.019 显著 $ TV $ 535.98 1 535.98 52.1 < 0.0001 显著 $ RV $ 20.23 1 20.23 1.97 0.1843 残差 133.73 13 10.29 总变异值 78837.22 19
下载: 导出CSV
表 6 屈服极限回归模型方差分析
Table 6. Variance analysis of yield limit of compressive strength regression model
平方和 自由度 均方值 F值 P值 是否显著 $ Q\left(T,R,V\right) $ 29.82 9 3.31 709.77 < 0.0001 显著 $ T $ 26.93 1 26.93 5769.72 < 0.0001 显著 $ R $ 0.0588 1 0.0588 12.61 0.0053 显著 $ V $ 0.4652 1 0.4652 99.65 < 0.0001 显著 $ TR $ 0.0069 1 0.0069 1.47 0.2534 $ TV $ 0.1378 1 0.1378 29.51 0.0003 显著 $ RV $ 0.1589 1 0.1589 34.03 0.0002 显著 $ {T}^{2} $ 1.87 1 1.87 401.02 < 0.0001 显著 $ {R}^{2} $ 0.005 1 0.005 1.08 0.3234 $ {V}^{2} $ 0.1421 1 0.1421 30.43 0.0003 显著 残差 0.0467 10 0.0047 总变异值 29.87 19
下载: 导出CSV
表 7 模型可信度检验分析
Table 7. Reliability test and analysis of the model
模型 标准差 相关系数 调整系数 变异系数/% 信噪比 $ E\left(T,R,V\right) $ 3.21 0.9983 0.9975 2.6 100.5393 $ Q\left(T,R,V\right) $ 0.0683 0.9984 0.9970 0.6376 72.3359
下载: 导出CSV
表 8 验证不同温度T、含碳量R以及空位率V下的仿真试验结果
Table 8. Verification of the simulation results under different temperatures T, carbon contents R and vacancy rates V
编号 组合 $ E $/GPa $ Q $/GPa 温度T/K 含碳量R/% 空位率V/% 1 300 1.9 1 205.1847 13.0851 2 500 1.9 2 156.9726 11.1803 3 500 1.9 4 166.5242 11.0399 4 700 1.9 3 99.7662 10.3489 5 900 1.9 5 85.7702 9.7070 6 300 1 1 192.1814 13.2412 7 500 1.3 4 160.2058 10.9185 8 500 2.2 3 164.0080 11.1295 9 700 1.6 1 85.3685 10.0065 10 900 1 2 42.6706 9.9332
下载: 导出CSV
表 9 仿真值与预测值误差
Table 9. The errors of simulation and prediction values
编号 $ E $ $ Q $ 绝对误差/GPa 相对误差/% 绝对误差/GPa 相对误差/% 1 0.99 0.48 0.09 0.66 2 3.88 2.47 0.16 1.47 3 1.01 0.60 0.25 2.30 4 9.04 9.06 0.57 5.46 5 0.39 0.45 0.04 0.43 6 2.73 1.42 0.34 2.58 7 0.39 0.24 0.16 1.50 8 0.72 0.44 0.30 2.72 9 1.27 1.48 0.29 2.90 10 0.35 0.83 0.10 1.05
下载: 导出CSV
表 10 优化结果预测值与仿真值
Table 10. Optimized results of the predicted values and simulation values
T/K R/% V/% $ E $ $ Q $ 预测
/GPa仿真
/GPa相对
误差/%预测
/GPa仿真
/GPa相对
误差/%750 1.018 1.004 71.108 70.349 1.067 10.442 10.220 2.126 800 1.004 1.120 58.572 59.145 0.978 10.266 10.153 1.101 850 1.063 1.499 49.431 50.017 1.185 9.996 10.092 0.960 900 1.000 2.000 42.317 42.671 0.837 9.829 9.933 1.058
下载: 导出CSV
-
[1] LI X, YIN Y H, ZHANG Y Z. Molecular dynamics Simulation of the effects of point defect type and concentration on plastic deformation behavior of α-Fe[J]. Rare Metal Materials and Engineering, 2022,51(8):2881-2891. (李翔, 尹益辉, 张元章. 点缺陷类型和浓度对α-Fe塑性变形行为影响的分子动力学模拟[J]. 稀有金属材料与工程, 2022,51(8):2881-2891.LI X, YIN Y H, ZHANG Y Z. Molecular dynamics Simulation of the effects of point defect type and concentration on plastic deformation behavior of α-Fe[J]. Rare Metal Materials and Engineering, 2022, 51（8）: 2881-2891. [2] WEI Z H, MA X, KE C B, et al. Molecular dynamics simulation of migration behavior of FCC-BCC atomic terrace-step phase boundary in iron-based alloy[J]. Acta Physica Sinica, 2020,69(13):242-254. (韦昭召, 马骁, 柯常波, 等. Fe合金FCC-BCC原子尺度台阶型马氏体相界面迁移行为的分子动力学模拟研究[J]. 物理学报, 2020,69(13):242-254.WEI Z H, MA X, KE C B, et al. Molecular dynamics simulation of migration behavior of FCC-BCC atomic terrace-step phase boundary in iron-based alloy[J]. Acta Physica Sinica, 2020, 69（13）: 242-254. [3] YUAN Y Q, ZENG X G, HU Y F. Molecular dynamics simulation for crack propagation of α-Fe under uniaxial tension and fatigue loading[J]. Journal of Xinyang Normal University(Natural Science Edition), 2016,29(1):31-37. (袁玉全, 曾祥国, 胡燕飞. 分子动力学模拟α-Fe拉伸与疲劳裂纹扩展机理[J]. 信阳师范学院学报(自然科学版), 2016,29(1):31-37.YUAN Y Q, ZENG X G, HU Y F. Molecular dynamics simulation for crack propagation of α-Fe under uniaxial tension and fatigue loading[J]. Journal of Xinyang Normal University(Natural Science Edition), 2016, 29（1）: 31-37. [4] WANG Y T, ZENG X G, YANG X. Molecular dynamics simulation of effect of temperature on void nucleation and growth of single crystal iron at a high strain rate[J]. Acta Physica Sinica, 2019, 68(24): 235-251. (王云天, 曾祥国, 杨鑫. 高应变率下温度对单晶铁中孔洞成核与生长影响的分子动力学研究[J]. 物理学报, 2019, 68(24): 235-251.WANG Y T, ZENG X G, YANG X. Molecular dynamics simulation of effect of temperature on void nucleation and growth of single crystal iron at a high strain rate[J]. Acta Physica Sinica, 2019, 68(24): 235-251. [5] CHENG Z X, WANG H, LIU G R. Fatigue crack propagation in carbon steel using RVE based model[J]. Engineering Fracture Mechanics, 2021,258(12):108050. [6] QU C C, LIU K R, HAN Q, et al. Optimization of Cu and Sc content in Al-Cu-Sc aluminum alloy conductor materials by response surface method[J]. Rare Metals and Cemented Carbides, 2021,49(04):43-49. (曲晨驰, 刘奎仁, 韩庆, 等. 响应面法优化Al-Cu-Sc铝合金导体材料Cu、Sc元素的含量[J]. 稀有金属与硬质合金, 2021,49(04):43-49.QU C C, LIU K R, HAN Q, et al. Optimization of Cu and Sc content in Al-Cu-Sc aluminum alloy conductor materials by response surface method[J]. Rare Metals and Cemented Carbides, 2021, 49（04）: 43-49. [7] HU J, ZHANG P L, WU L, et al. Study on mechanical properties of cementitious matrix based on response surface method and optimization of the fitting ratio[J]. Materials Reports, 2022,36(S2):173-177. (胡静, 张品乐, 吴磊, 等. 基于响应面法的ECC基体力学性能研究与配合比优化[J]. 材料导报, 2022,36(S2):173-177.HU J, ZHANG P L, WU L, et al. Study on mechanical properties of cementitious matrix based on response surface method and optimization of the fitting ratio[J]. Materials Reports, 2022, 36（S2）: 173-177. [8] HEPBURN D J, ACKLAND G J. Metallic-covalent interatomic potential for carbon in iron[J]. Physical Review B, 2008,78(16):165115. [9] YE T Z, YAO H, WU Y W, et al. Molecular dynamics study on tensile mechanical properties of FeCrAl alloy[J]. Rare Metal Materials and Engineering, 2023,52(2):777-784. (叶天舟, 姚欢, 巫英伟, 等. FeCrAl合金拉伸力学性能分子动力学研究[J]. 稀有金属材料与工程, 2023,52(2):777-784.YE T Z, YAO H, WU Y W, et al. Molecular dynamics study on tensile mechanical properties of FeCrAl alloy[J]. Rare Metal Materials and Engineering, 2023, 52（2）: 777-784. [10] Standard for design of steel structures GB 50017-2017[S]. Beijing: China Architecture and Construction Press, 2017. (钢结构设计标准: GB50017-2017[S]. 北京: 中国建筑工业出版社, 2017.Standard for design of steel structures GB 50017-2017[S]. Beijing: China Architecture and Construction Press, 2017. -
下载:
点击查看大图
计量
- 文章访问数: 39
- HTML全文浏览量: 24
- PDF下载量: 11
- 被引次数: 0
