GH3128蠕变损伤模型预测以及有限元模拟

康晓东; 田子航; 刘泳; 张申; 方龙飞

doi:10.7513/j.issn.1004-7638.2025.01.023

GH3128蠕变损伤模型预测以及有限元模拟

doi: 10.7513/j.issn.1004-7638.2025.01.023

康晓东^1,,
田子航^{1, 2},
刘泳¹,
张申¹,
方龙飞¹

1.
沈阳化工大学机械与动力工程学院, 辽宁沈阳 110142
2.
中国科学院沈阳自动化研究所, 辽宁沈阳 110016

详细信息

作者简介:
康晓东，1998年出生，男，山西大同人，硕士，研究方向：金属材料的力学性能，E-mail：kxdkyb05@126.com

中图分类号: TF76,TG132.3
计量
- 文章访问数: 31
- HTML全文浏览量: 18
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2024-01-03
- 刊出日期: 2025-02-27

Creep damage model prediction and finite element simulation of GH3128

1.
School of Mechanical and Power Engineering, Shenyang University of Chemical Technology, Shenyang 110142, Liaoning, China
2.
Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, Liaoning, China

摘要

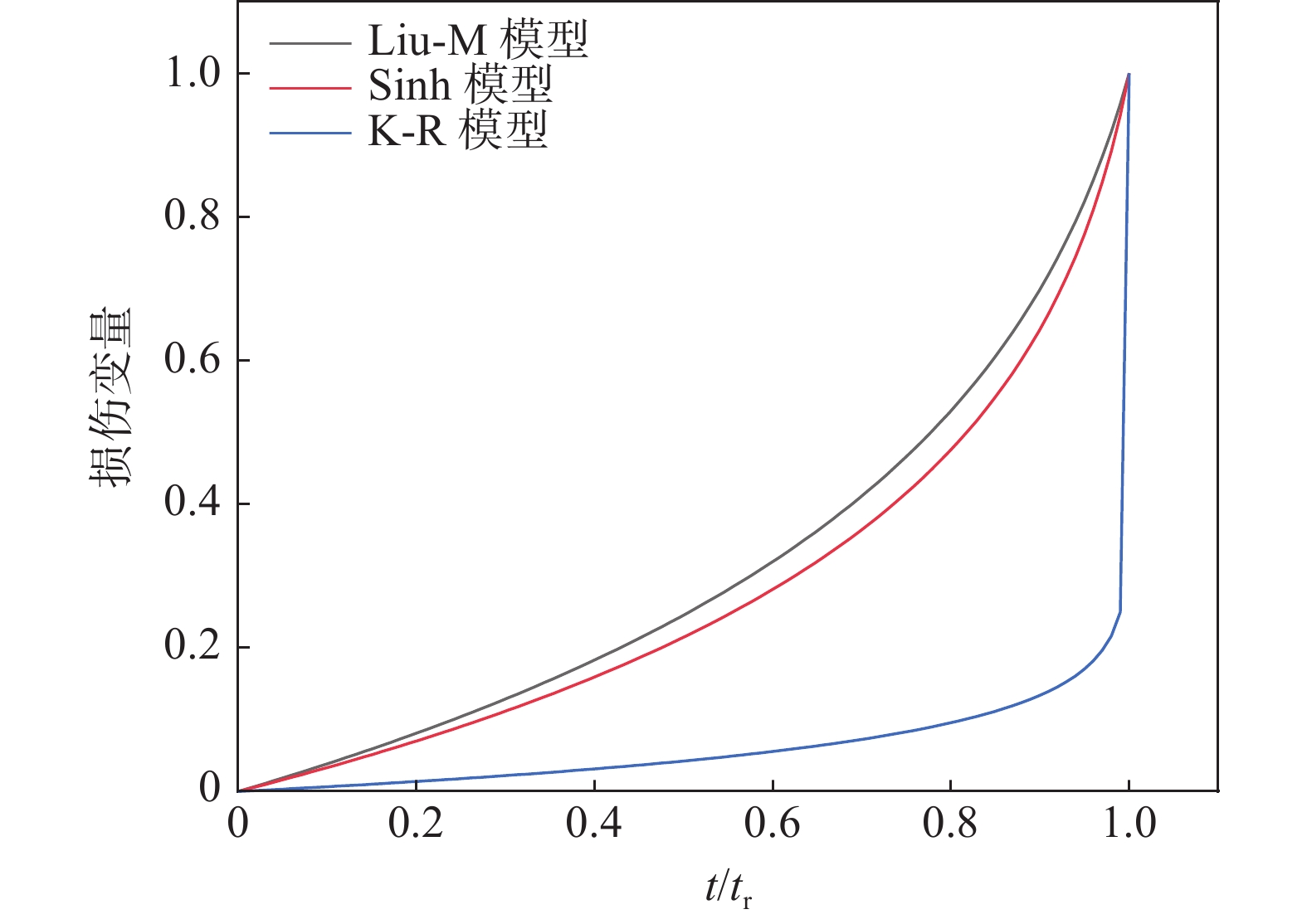
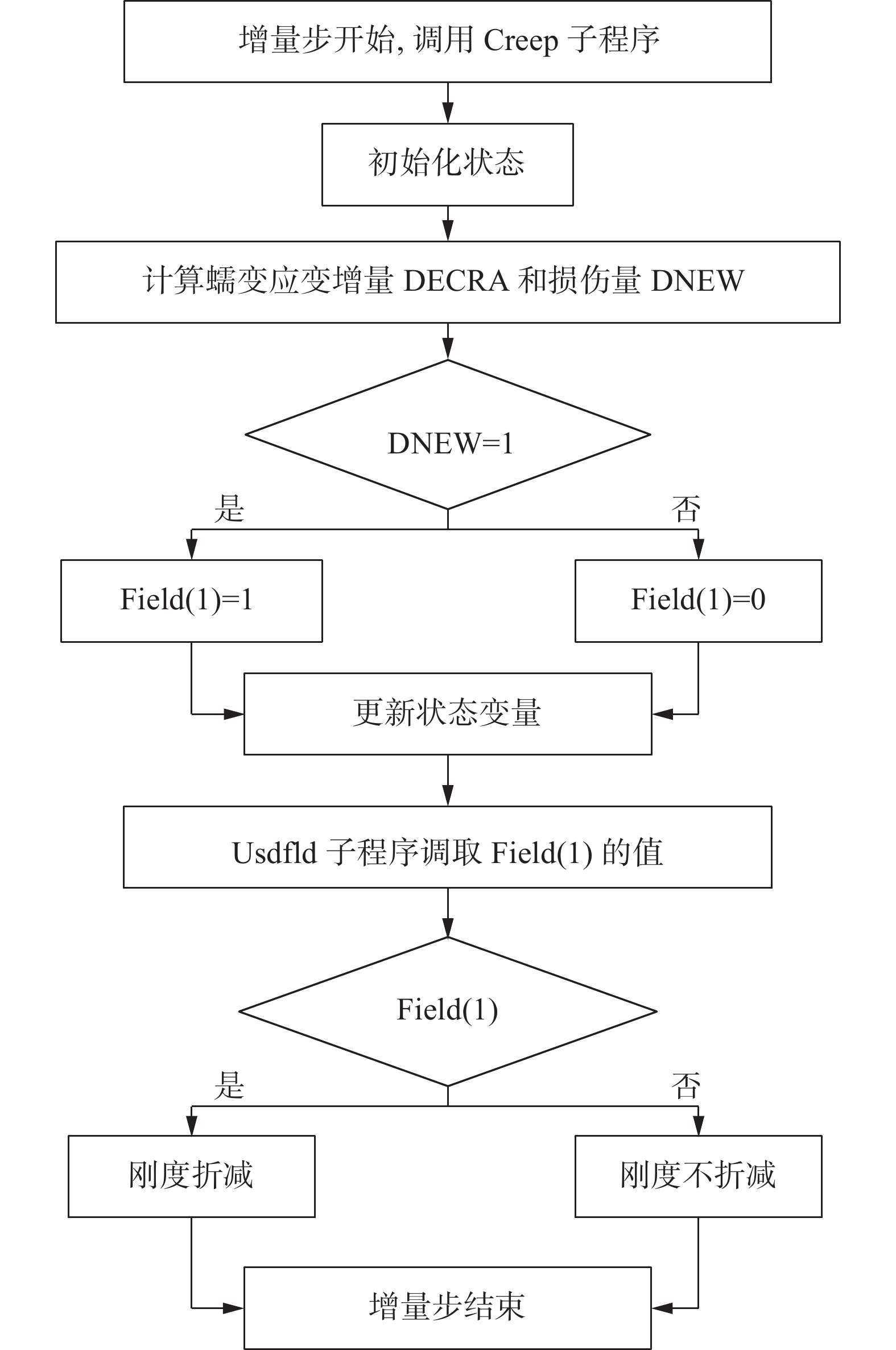
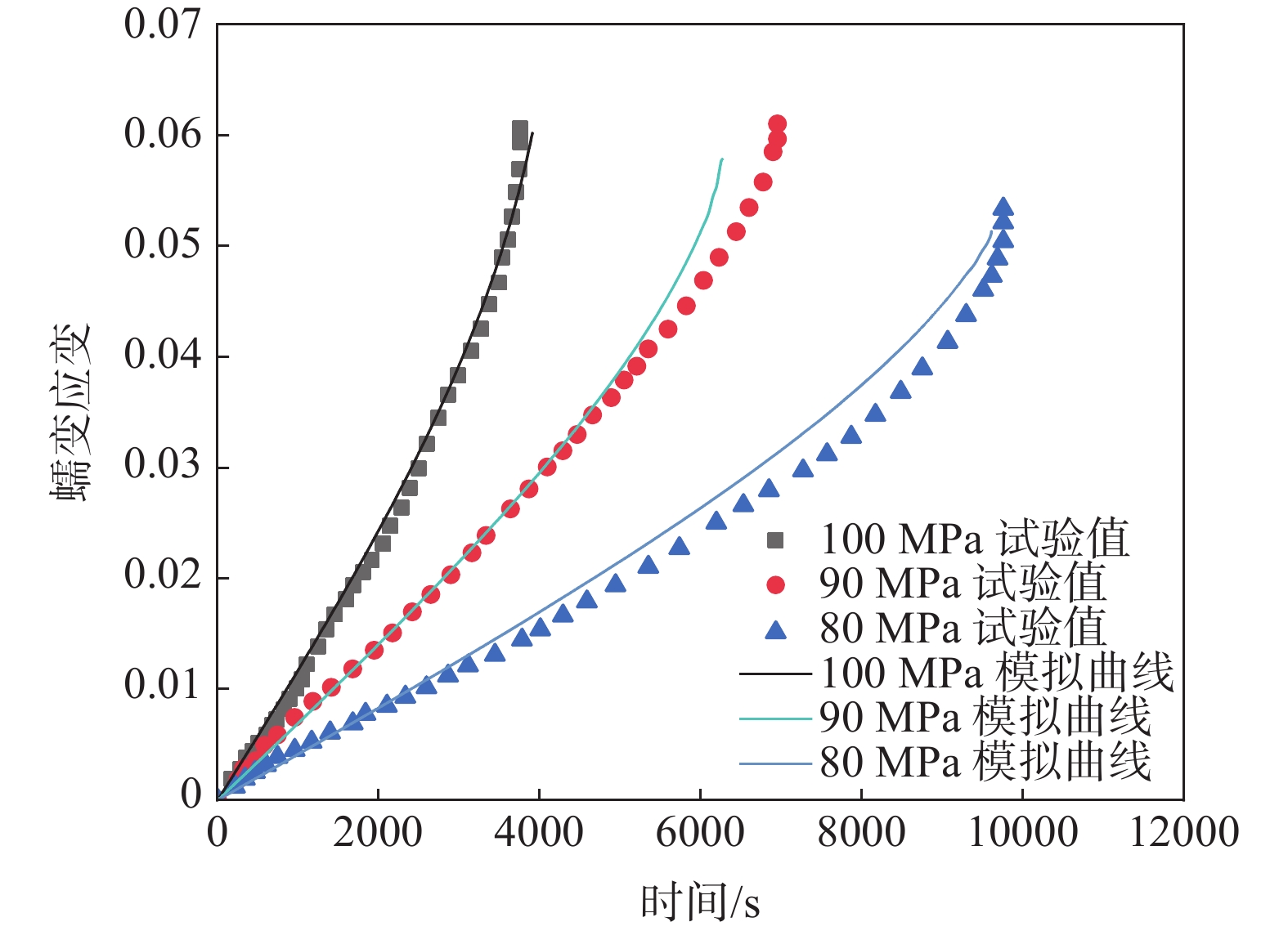
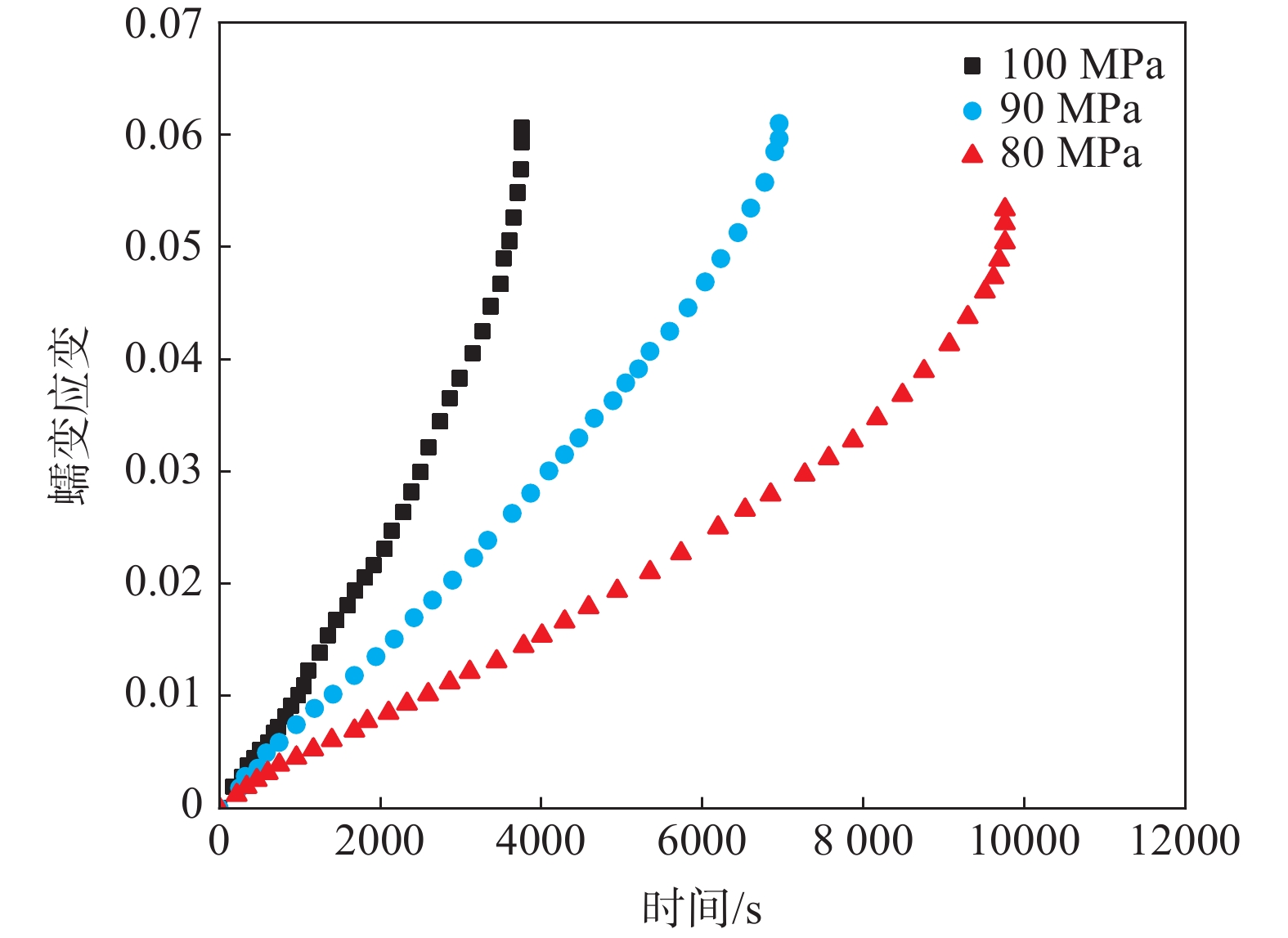
摘要: 从蠕变损伤方程构建和有限元模拟两方面对GH3128合金在950 ℃条件下的高温蠕变行为进行分析。首先，结合K-R模型、Sinh模型及Liu-M模型进行蠕变损伤方程构建，继而对模型寿命预测和损伤行为进行对比分析，发现应力100、90 MPa和80 MPa下寿命预测相对误差最大仅为10.8%，累积相对误差Sinh模型最小为18.3%。而对损伤行为的对比发现Sinh模型和Liu-M模型较K-R模型损伤演化过程要缓和，有利于在有限元模拟时网格的划分，由此得出：对GH3128合金蠕变行为预测效果最好的是Sinh模型。最后，利用ABAQUS软件中Creep子程序接口，通过二次开发编写Sinh模型，有限元模拟的结果表明Sinh模型对GH3128合金蠕变行为分析较为准确和高效。
- 损伤模型 /
- 材料蠕变 /
- 二次开发 /
- ABAQUS软件
Abstract: Creep damage equation construction and finite element simulation were used to analyze the high temperature creep behavior of GH3128 alloy at 950 ℃. Firstly, the creep damage equation was constructed by combining the K-R model, the Sinh model and the Liu-M model. Then the life prediction and damage behavior of the model were compared and analyzed. It is found that the maximum relative error of life prediction under 100, 90 MPa and 80 MPa is only 10.8%. The cumulative relative error of the Sinh model was the smallest with the value of 18.3%. The comparison of damage behaviors shows that the damage evolution processes of the Sinh model and the Liu-M model are slower than that of the K-R model, which is beneficial to the meshing in finite element simulation. Therefore, it is concluded that the Sinh model has the best prediction effect on the creep behavior of GH3128 alloy. Finally, the Creep subroutine interface in ABAQUS software was used to program the Sinh model through secondary development. The results of finite element simulation showed that the Sinh model was relatively accurate and efficient in analyzing the creep behavior of GH3128 alloy.
- damage model /
- Creep of the material /
- Secondary development /
- ABAQUS software

HTML全文

0. 引言

无取向硅钢中析出物的粒径为0.1～1 μm时，会导致最终的磁性能降低^[1−4]。分析其原因，是百纳米级夹杂物的存在阻碍了磁畴壁（尺寸为100～900 nm）的正常移动^[5−7]，使得晶粒不能正常长大^[8−10]，最终降低了无取向硅钢产品的磁性能^[11]。Boc I 等人^[7]的研究得到了以下结论：夹杂物粒子在0.005～0.5 μm范围和直径＞0.5 μm或者＜0.005 μm的粒子分别进行比较，结果得出0.005～0.5 μm粒径对磁性能重要得多。

文献[4]介绍了高牌号硅钢的硫化物和氮化物的析出热力学计算，但是由于高端牌号硅钢本身的保密性，即使不同企业同一牌号硅钢成分之间也并不一致，尤其针对Al、Mn等额外添加的合金元素，此外S和N的含量也体现了各个企业炼钢水平的高低，上述成分之间差距均较大。

为此，笔者以国内某厂的高牌号无取向硅钢50W350中的MnS、Cu₂S、AlN和TiN为例，针对具体生产单位的高牌号中硫、氮化物等展开热力学分析，从热力学角度研究了无取向硅钢生产过程中析出物的规律。

1. 热力学计算推导

由于热力学计算获得的是平衡浓度积和温度之间的关系，进而可以得到具体硫、氮化物的析出温度，这对现场理论指导有重要意义。

由于MnS、Cu₂S、AlN和TiN随着钢水降温过程中溶解度逐渐发生变化，且固液相之间变化趋势不同，因此当实际溶度积(Q)大于平衡溶度积(K)时，意味着析出物开始析出。钢中的金属M（铝、锰等）与非金属X（氮、硫）残余反应生成MX。在反应过程中平衡常数的计算如式（1）所示。

$$ K\mathrm{_{eq}}=\dfrac{a_{\mathrm{M}\mathrm{X}}}{a_{\mathrm{M}}a_{\mathrm{X}}}=\dfrac{1}{f_{\mathrm{M}}\left[\mathrm{\%}\mathrm{M}\right]f_{\mathrm{X}}\left[\mathrm{\%}\mathrm{X}\right]} $$

(1)

式中， [%M]为金属质量百分含量； [%X]为氮、硫的质量百分数；f_M为金属元素活度系数；f_X为氮、硫的活度系数。

根据MX反应的$ \Delta {G}^{{\theta }} $数据可得：

$$ \mathrm{l}\mathrm{g}{K}_{\mathrm{e}\mathrm{q}}=-\dfrac{\Delta {G}^{{\theta }}}{2.3RT}=B-\dfrac{A}{T} $$

(2)

式(1)取对数，代入式（2）可得式（3）：

$$ \mathrm{lg}\left[\mathrm{\%}\mathrm{M}\right]+\mathrm{lg}\left[\mathrm{\%}\mathrm{X}\right]+\mathrm{l}\mathrm{g}{f}_{\mathrm{M}}+\mathrm{l}\mathrm{g}{f}_{\mathrm{X}}=B-\dfrac{A}{T} $$

(3)

式中，B代表$ \dfrac{\Delta S}{2.3 R} $计算得到的具体数值，其中$ \Delta S $为熵变，R为8.314 J/(mol·K)； A代表$ \dfrac{\Delta H}{2.3 R} $计算得到的具体数值，其中$ \Delta H $为焓变。

由于钢中有关MnS、Cu₂S、AlN和TiN生成反应的$ \mathrm{l}\mathrm{g}{f}_{\mathrm{M}}、\mathrm{l}\mathrm{g}{f}_{\mathrm{X}} $值对式（3）中B值的影响很小，可以将式（3）转换为式（4）。

$$ \mathrm{lg}\left[\mathrm{\%}\mathrm{M}\right]\left[\mathrm{\%}\mathrm{X}\right]=-\dfrac{\Delta {G}^{\theta }}{2.3RT}=B-\dfrac{A}{T} $$

(4)

经过上述公式的推导，可以获得具体的B和A，此外也可获得平衡溶度积K和实际溶度积Q，如表1所示。

表 1 AlN、MnS在钢中的溶度积^[2−3]

Table 1. Solubility product of AlN and MnS in steel^[2−3]

化合物	K	Q	相
AlN	6.334-14069/T	[%Al][%N]	液相
MnS	4.63-8750/T	[%Mn][%S]	液相
AlN	5.37-14640/T	[%Al][%N]	δ相
AlN	2.27-10590/T	[%Mn][%S]	δ相
Cu₂S	26.31-44791/T	[%Cu]²[%S]	液相+δ相
TiN	5.56-17025/T	[%Ti][%N]	液相+δ相

下载: 导出CSV

| 显示表格

当钢水温度降低到两相区时，钢中的溶质元素等元素发生偏析，此时氮、硫的含量及锰、铝元素的含量分别用式（5）（6）计算。

$$ \left[\mathrm{\%}\mathrm{X}\right]=\dfrac{{\left[\mathrm{\%}\mathrm{X}\right]}_{0}}{{f}_{\mathrm{s}}\left({k}_{\mathrm{X}}-1\right)+1} $$

(5)

$$ \left[\mathrm{\%}\mathrm{M}\right]={\left[\mathrm{\%}\mathrm{M}\right]}_{0}{(1-{f}_{\mathrm{s}})}^{{k}_{\mathrm{M}}-1} $$

(6)

式中， f_s为固相百分率；k_M为金属元素M的平衡溶质分配因数；k_X为非金属X的平衡溶质分配因数；析出物形成实际的浓度积Q_MX可表示为^[4]：

$$ Q_{\mathrm{MX}}=[\% \mathrm{M}][\% \mathrm{X}]=\frac{[\% \mathrm{M}]_0[\% \mathrm{X}]_0\left(1-f_{\mathrm{s}}\right)^{k_{\mathrm{M}}-1}}{f_{\mathrm{s}}\left(k_{\mathrm{X}}-1\right)+1} $$

(7)

温度T与固相百分率f_s的关系如式（8）表示。

$$ {f}_{\mathrm{s}}=\frac{({T}_{\mathrm{F}\mathrm{e}}-{T}_{\mathrm{s}})({T}_{\mathrm{l}}-T)}{({T}_{\mathrm{l}}-{T}_{\mathrm{s}})({T}_{\mathrm{F}\mathrm{e}}-T)} $$

(8)

式中， T为凝固过程中液相温度，K；T_Fe为纯铁的熔点（1 809 K）；T_L为液相线温度，K；T_S为固相线温度，K。

2. 热力学计算条件

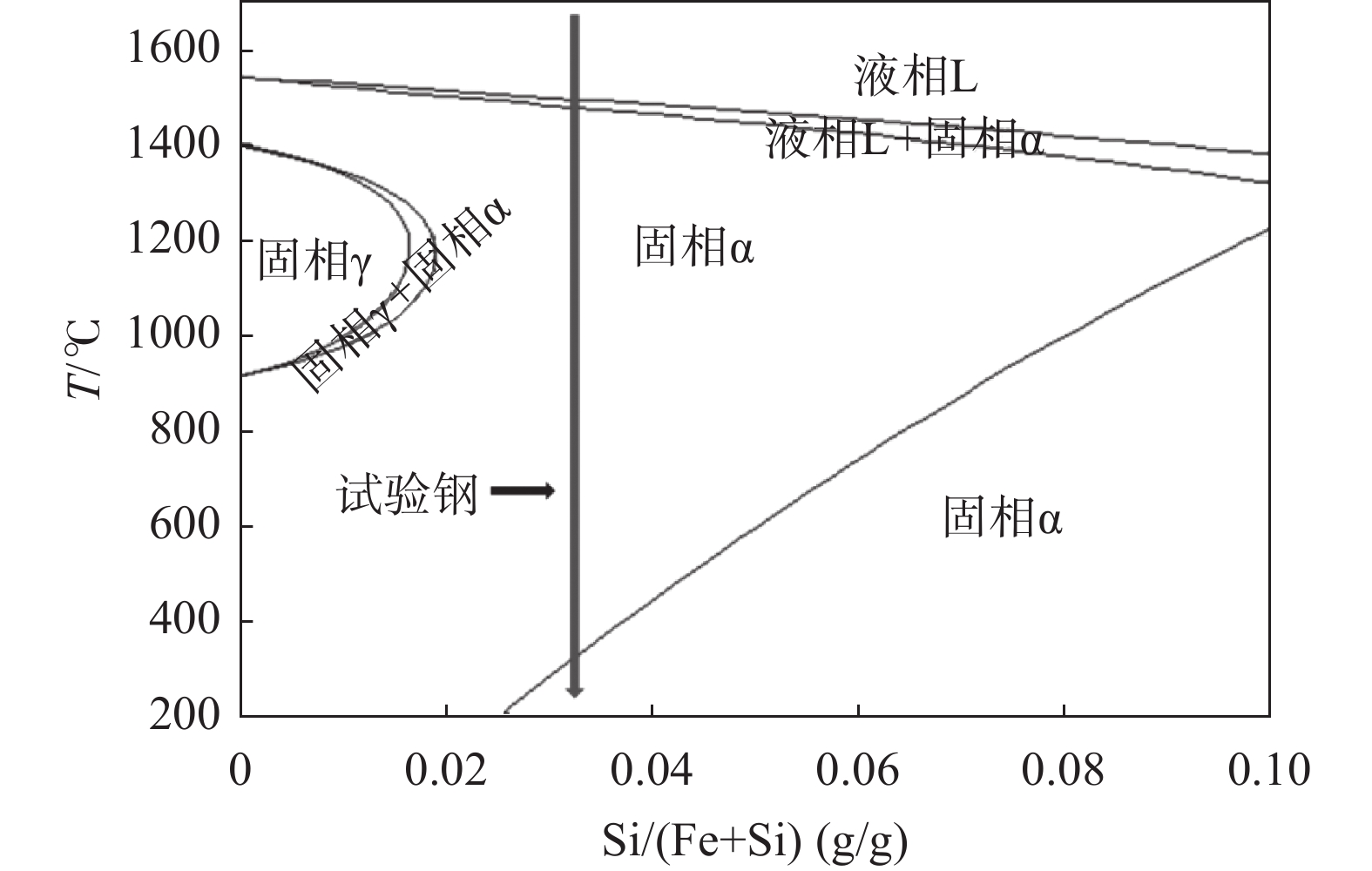
计算钢种为模拟高牌号典型无取向硅钢种50W350，其主要化学成分如表2所示。分别通过FactSage软件Phase Diagram相图计算模块，其在铁硅相图中位置如图1所示，绿色线代表试验钢在相图中的具体位置。表3为各个阶段的平衡溶质分配因数和液相线。

表 2 试验钢的主要化学成分

Table 2. Main chemical composition of the tested steel %

C	Mn	Si	S	P	Als	N	Ti	Cu
0.0019	0.32	2.72	0.0023	0.014	0.5016	0.0015	0.0026	0.046

下载: 导出CSV

| 显示表格

图 1 Fe-Si二元相图 ( FactSage software)

Figure 1. Fe-Si binary phase diagram ( FactSage software)

下载: 全尺寸图片幻灯片

表 3 凝固过程中AlN、MnS参数选择^[3]

Table 3. Selection of AlN and MnS parameters during solidification process^[3]

Fe熔点/K	液相线		固相线		平衡溶质分配因数
Fe熔点/K	温度/K	（Si+Al)/%	温度/K	（Si+Al)/%	k_N	k_Al	k_S	k_Mn	k_Ti	k_Cu
1 809	1788	3.2	1768	3.2	0.28	0.92	0.1	0.74	0.3	0.9

下载: 导出CSV

| 显示表格

液相线和固相线采用如下公式计算^[4]：

$${\begin{split} & {T_{\mathrm{L}}} = 1536 + 273 - \Big\{ [90[\% {\mathrm{C}}] + 6.2[\% {\mathrm{Si}}] + 1.7[\% {\mathrm{Mn}}] + \\ & 28\left[ {\% {\mathrm{P}}} \right] + 40\left[ {\% {\mathrm{S}}} \right] + 2.6[\% {\mathrm{Cu}}] + 2.9[\% {\mathrm{Ni}}] + 1.8[\% {\mathrm{Cr}}] +\\ & 5.1[\% {\mathrm{Al}}]\Big\} \\[-16pt] \end{split}} $$

(9)

$$ {\begin{split} &{T_{\mathrm{s}}} = 1536 + 273 - \{ [415.3[\% {\mathrm{C}}] + 12.3[\% {\mathrm{Si}}] +6.8 \\ & [\% {\mathrm{Mn}}] +124.5\left[ {\% P} \right] + 183.9\left[ {\% S} \right] + 1.4[\% {\mathrm{Cu}}] +4.3\\ & [\% {\mathrm{Ni}}] +1.4[\% {\mathrm{Cr}}] + 4.1[\% {\mathrm{Al}}]\}\\[-16pt] \end{split}} $$

(10)

3. 热力学计算结果

3.1 液相计算结果

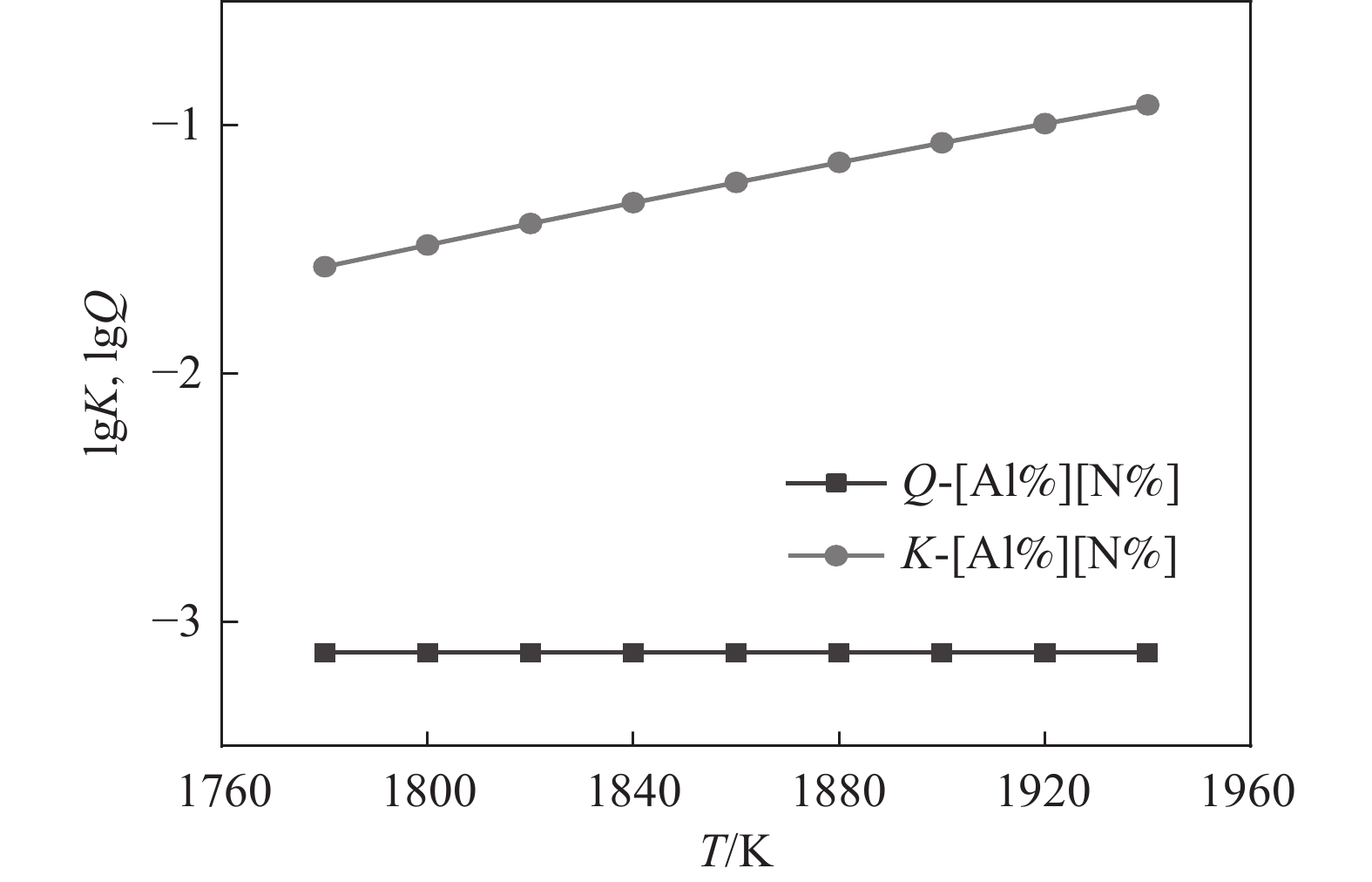
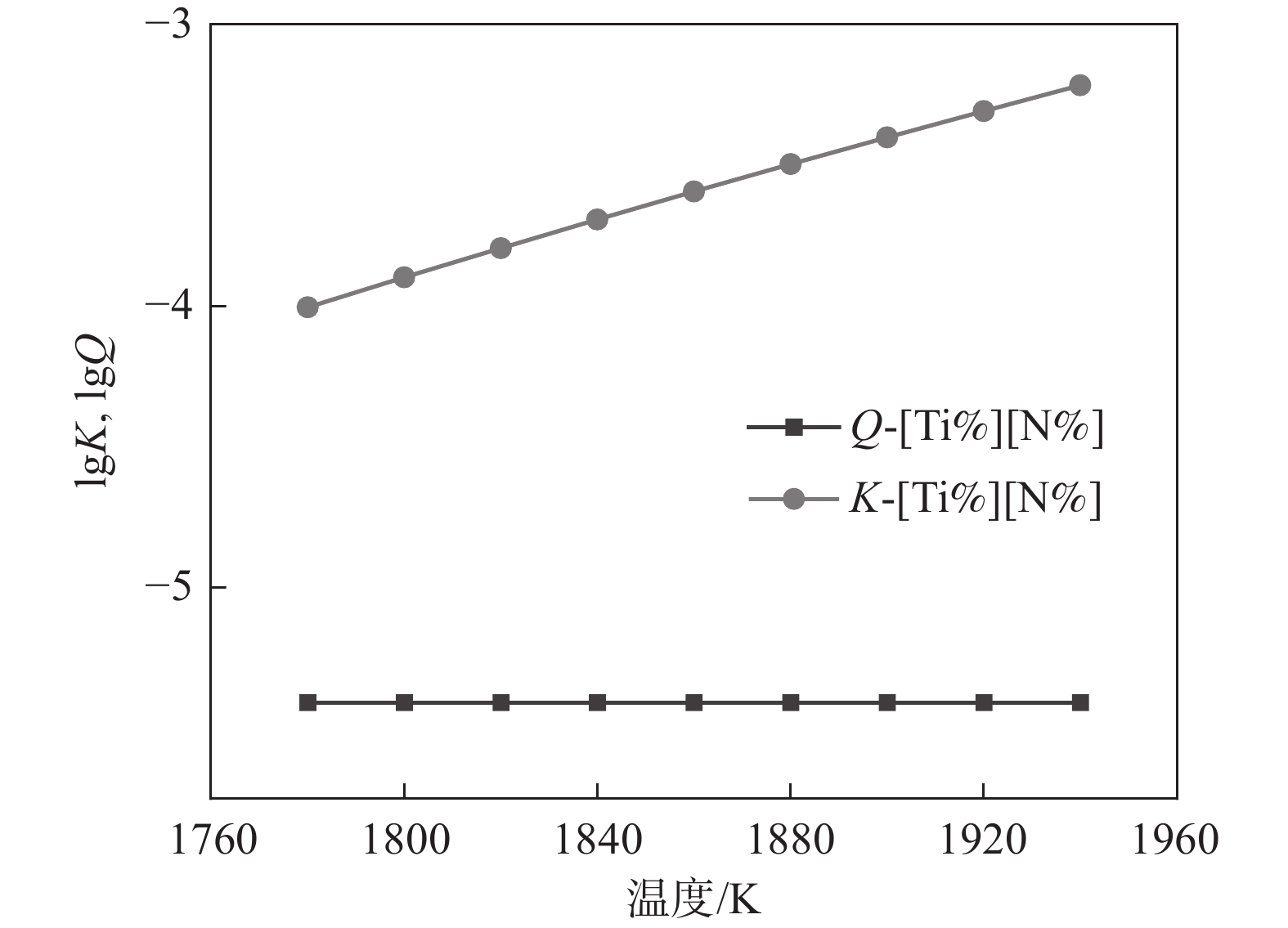
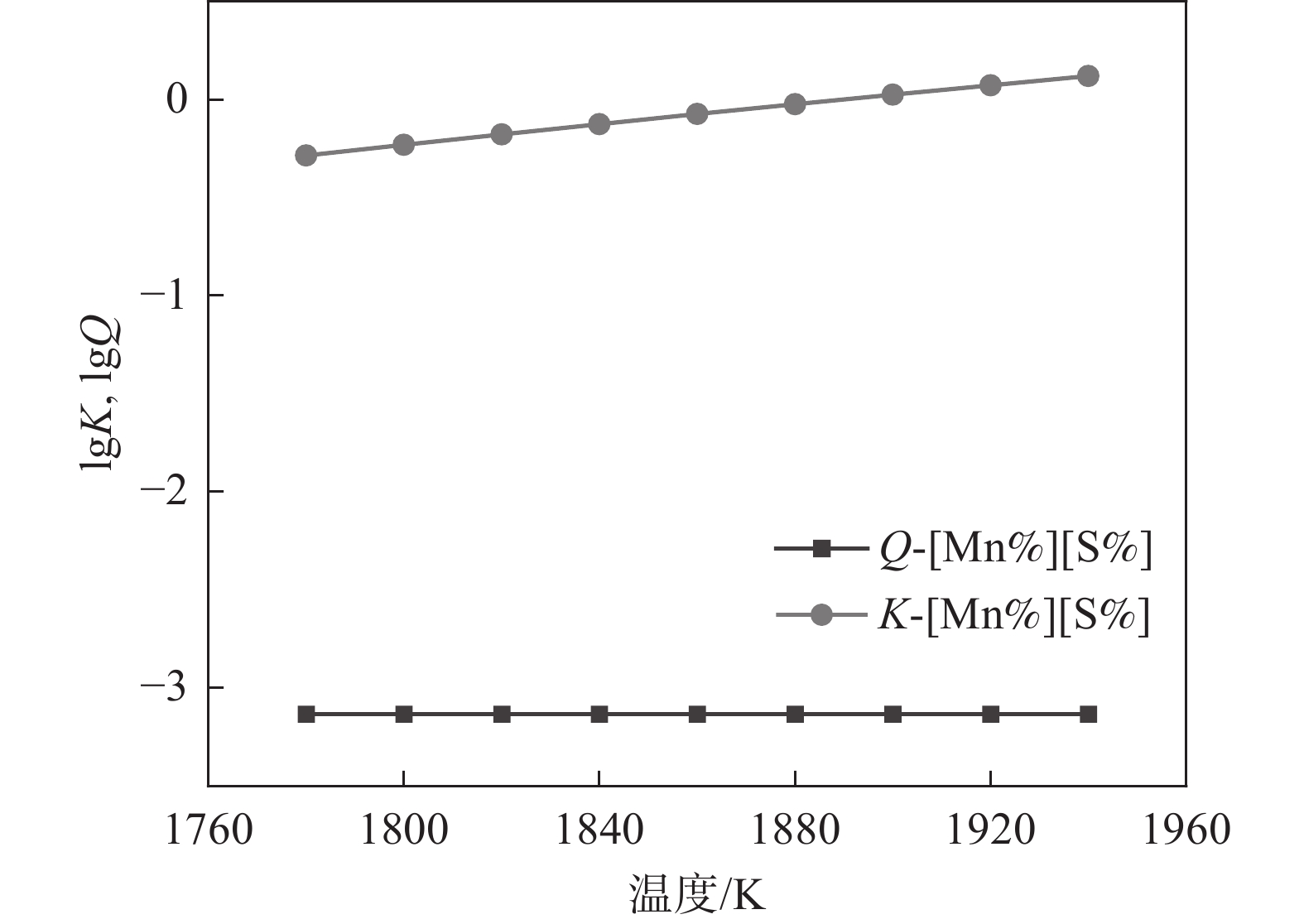
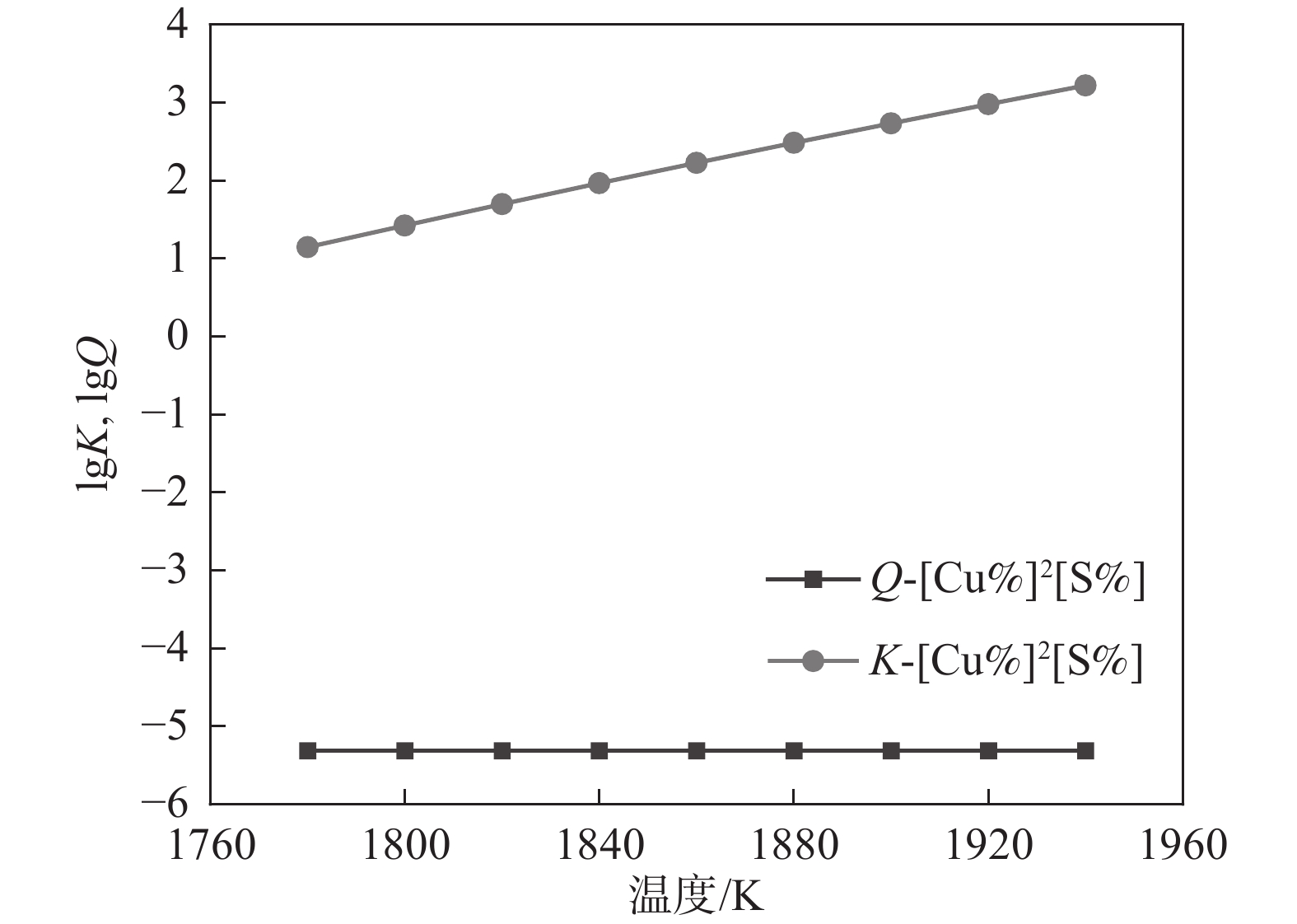
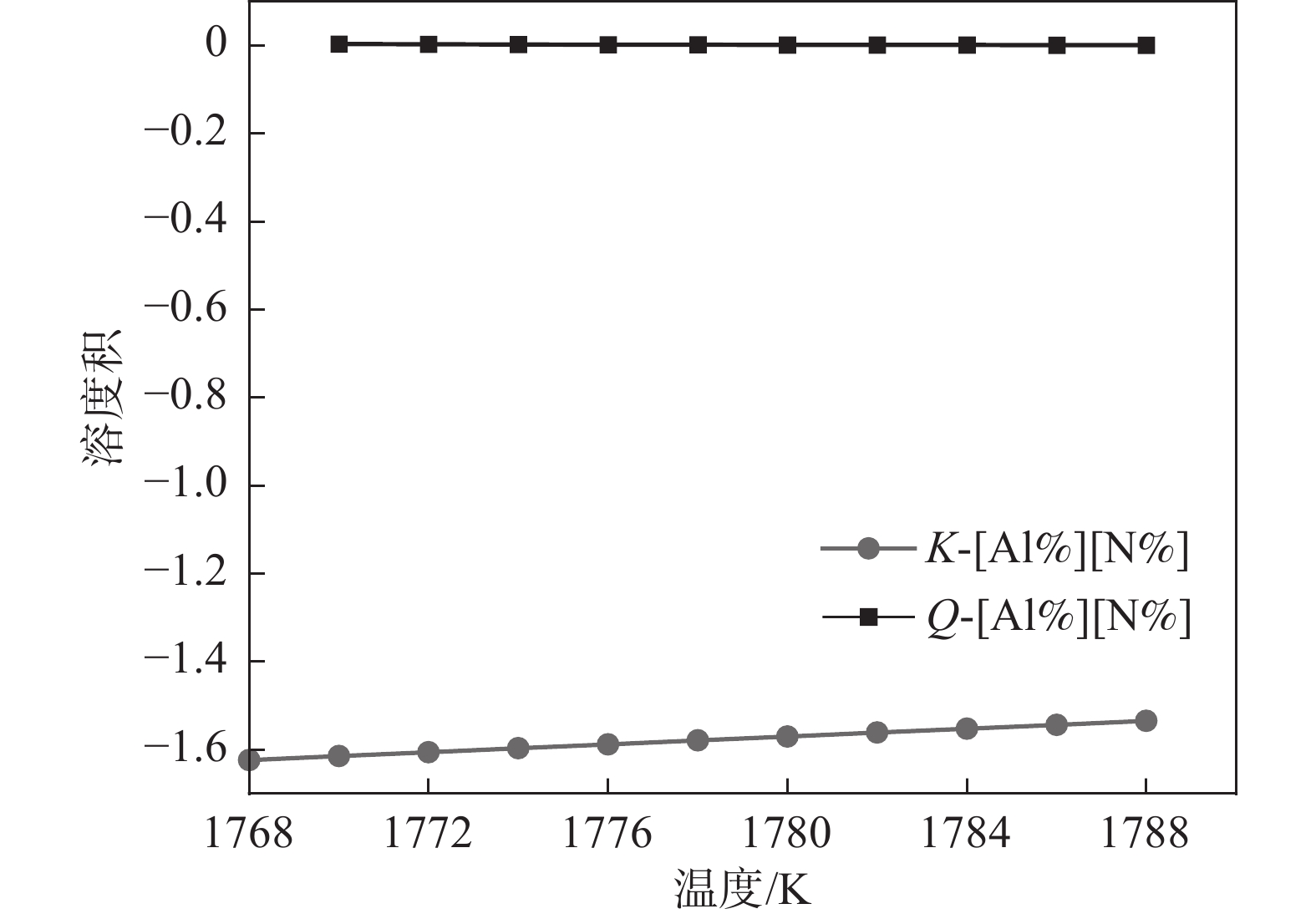
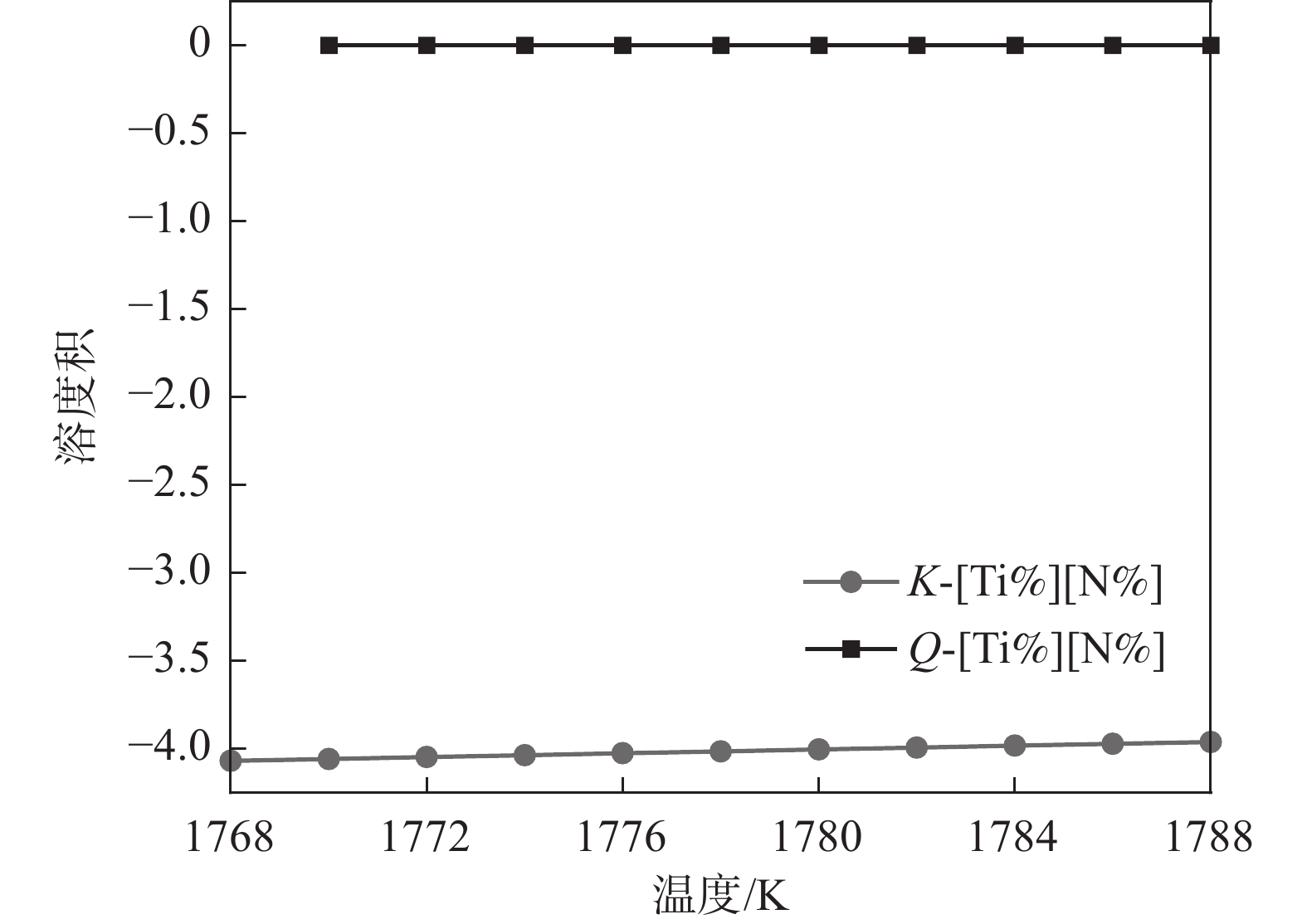
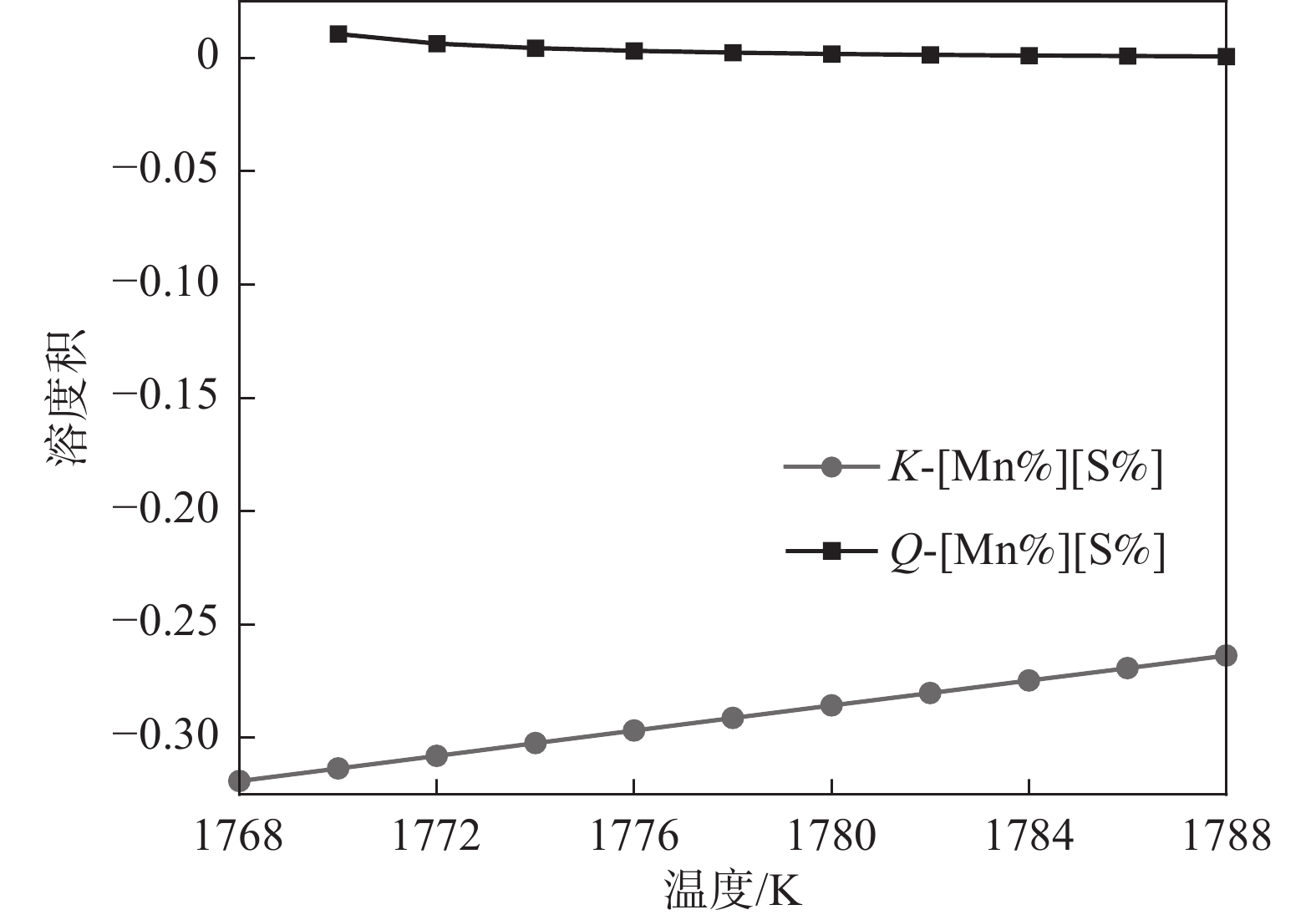
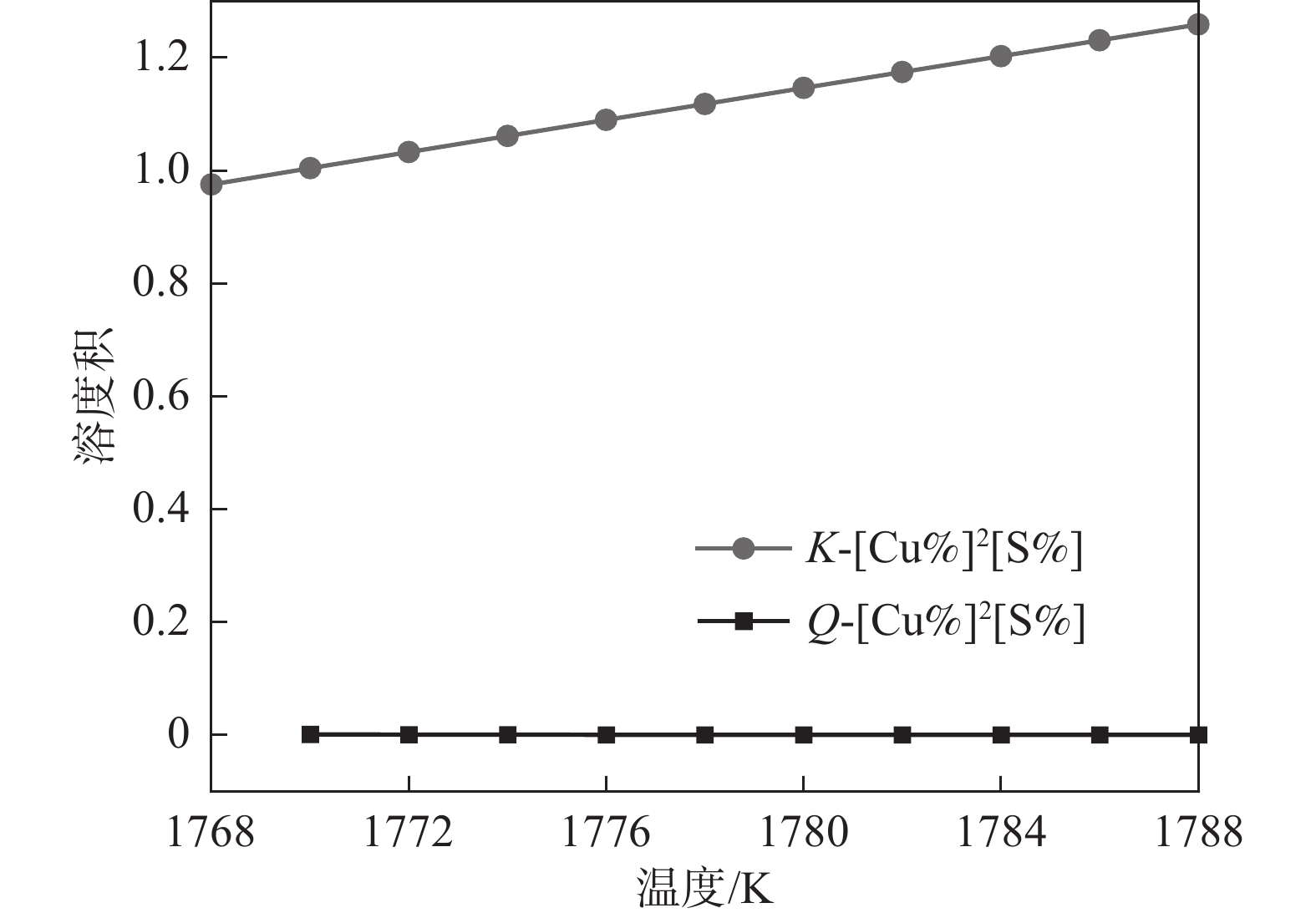
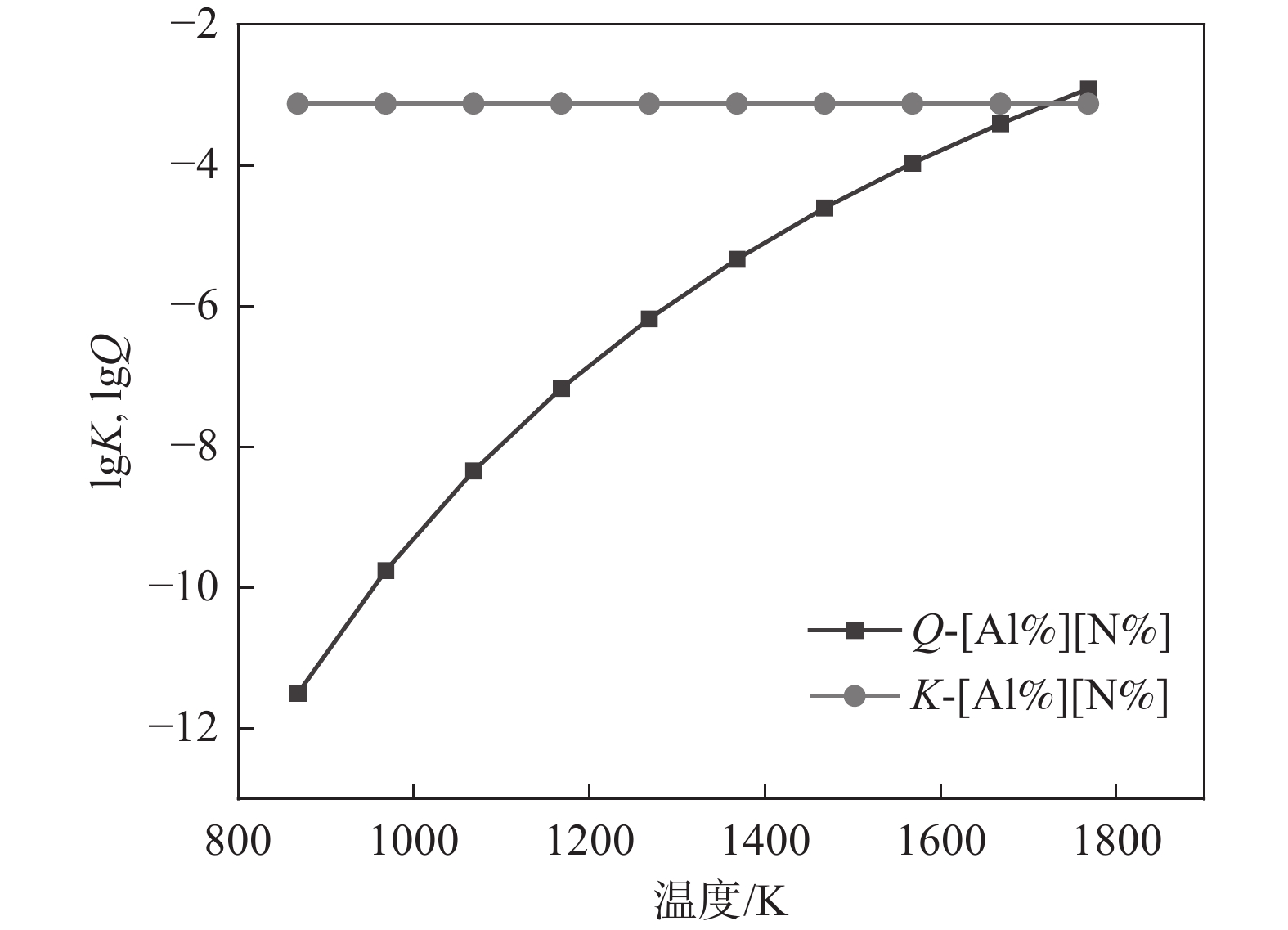
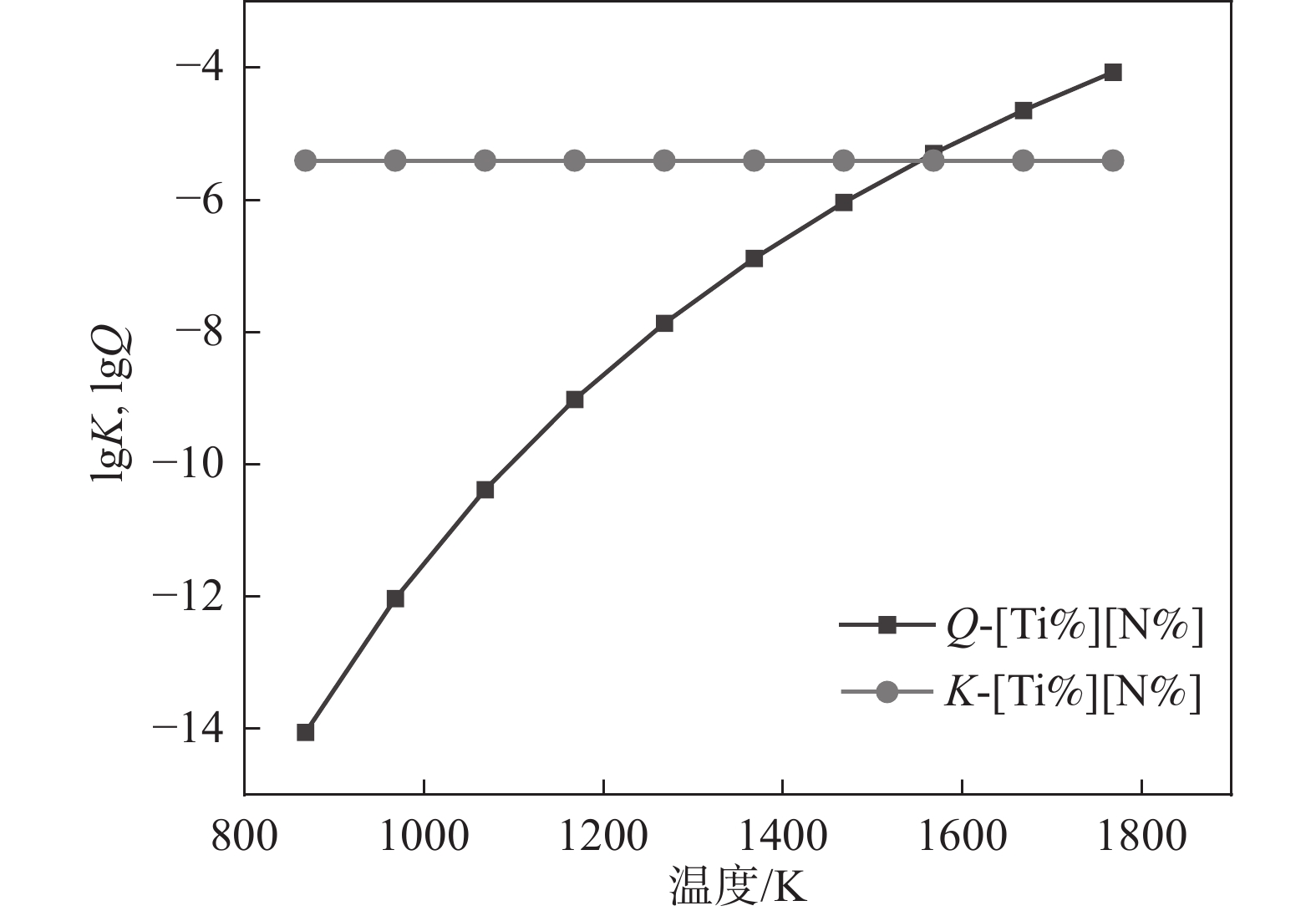
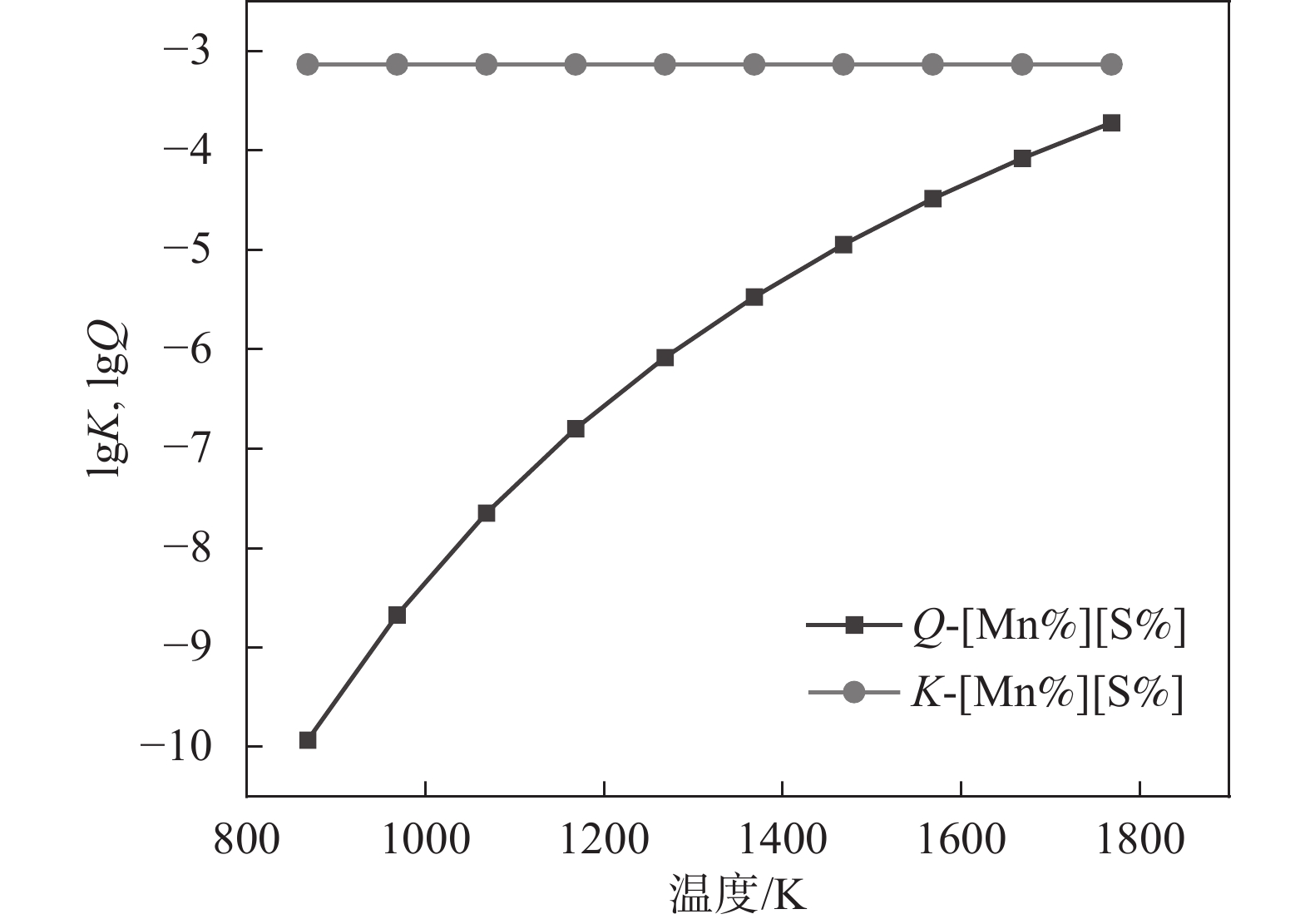
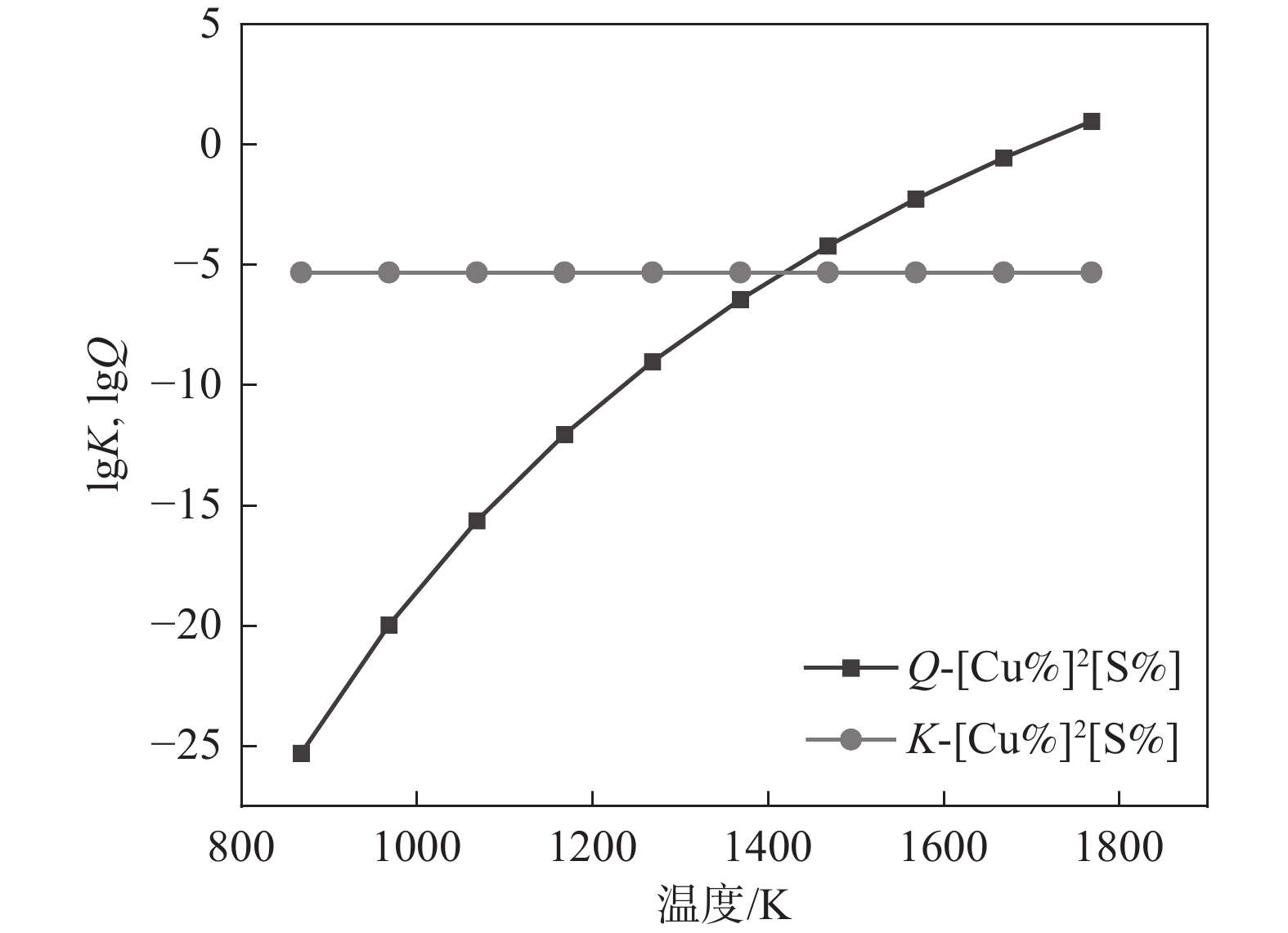
从表3可以看出，液相线1788 K，因此本小节计算的结果是温度在1788 K以上的部分。将热力学数据代入式（4）得出AlN、TiN、MnS和Cu₂S在钢液中的平衡溶度积。图2～5中为平衡溶度积和实际溶度积取对数。从表1可以看出，平衡溶度积与温度T呈现正相关关系，图2～5中曲线K对此可以作出相关解释。钢中温度从液相线1788 K上升到1 940 K，AlN平衡溶度积K的取值范围为−1.57～−0.91，MnS的平衡溶度积K取值在−0.29～0.11；AlN和MnS的Q和K两条曲线均没有交集，且Q值始终小于K，即AlN和MnS都不可能析出。同理对TiN和Cu₂S进行相关分析，两者的Q都小于K，都不能析出。

图 2 AlN在钢液中溶度积关系

Figure 2. Solubility product of AlN in liquid steel

下载: 全尺寸图片幻灯片

图 3 TiN在钢液中溶度积关系

Figure 3. Solubility product of TiN in liquid steel

下载: 全尺寸图片幻灯片

图 4 MnS在钢液中的溶度积关系

Figure 4. Solubility product of MnS in liquid steel

下载: 全尺寸图片幻灯片

图 5 Cu₂S在钢液中溶度积关系

Figure 5. Solubility product of Cu₂S in liquid steel

下载: 全尺寸图片幻灯片

3.2 凝固过程分析

50W350牌号无取向硅钢凝固过程中不存在γ相，这一点从图1中可以看出，因此只需要计算L→α和完全α即可。从表3可以看出，固相线温度为1768 K，液相线温度为1788 K，由于凝固阶段包含固液相温度区间以及完全α阶段，即L→α阶段，即1768～1788 K和固相线温度以下部分完全α阶段，即小于1768 K。

3.2.1 L→α阶段

根据溶度积公式计算，将固液相线代入公式（8），得到固相率$ \mathrm{\mathit{f}}_{\mathrm{s}} $，再将固相率代入公式（7），就可以得到实际平衡浓度积Q。图6～9为相关氮化物、硫化物溶度积曲线。

图 6 凝固过程中AlN析出溶度积关系

Figure 6. Relationship of solubility product of AlN precipitation and temperature during solidification process

下载: 全尺寸图片幻灯片

图 7 凝固过程中TiN析出溶度积关系

Figure 7. Relationship of solubility product of TiN precipitation and temperature during solidification process

下载: 全尺寸图片幻灯片

图 8 凝固过程中MnS析出溶度积关系

Figure 8. Relationship of solubility product of MnS precipitation and temperature during solidification process

下载: 全尺寸图片幻灯片

图 9 凝固过程中Cu₂S析出溶度积关系

Figure 9. Relationship of solubility product of Cu₂S precipitation and temperature during solidification process

下载: 全尺寸图片幻灯片

AlN的溶度积关系如图6所示。可以看出Q和K曲线没有交点，且Q始终能够高于K，这说明实际溶度积高于平衡溶度积，即次过程有AlN析出。此外，从Q的变化趋势也可以知道，液相向固相转换过程中，溶质元素Al和N逐渐增高，因此其溶度积也在逐渐增加，从1768 K时的0.023增加到1788 K时的0.029。由于Q＞K，AlN在此温度范围内可以析出。

由图7可知，从1788 K降温到1770 K，在此过程中Q和K没有交点，但是Q始终大于K，这表明TiN在1788～1788 K温度范围内是可以析出的。

综上所述，液相线和固相线之间的MnS溶度积关系如图8所示， MnS的Q和K曲线没有交点，但Q始终高于K，即MnS在此温度范围内是可以析出的。

同理，液相线和固相线之间的Cu₂S溶度积关系如图9所示，Cu₂S的Q和K曲线没有交点，且Q始终低于K值，此种情况下Cu₂S不具备析出热力学条件。

3.2.2 完全α阶段

图10～13为高牌号50ZW350无取向硅钢凝固过程到完全α阶段，氮化物和硫化物的析出溶度关系。由图10可知，K和Q曲线相交点的横坐标为1700 K，即保持Q大于K的温度范围必须是1700 K以上，在此范围内AlN可以从凝固过程中析出。而TiN的Q和K曲线相交点横坐标为1588 K（见图11），也就是1588 K温度范围以上，TiN是能够从凝固过程中析出的。而MnS的Q和K不相交，且Q数值小于K（见图12），即MnS在此温度范围内不可能析出。Cu₂S的Q和K曲线相交点的横坐标为1420 K（见图13），且在温度1420 K以上Q大于K时，Cu₂S是可以析出的。

图 10 凝固过程中AlN析出溶度积关系

Figure 10. Relationship of solubility product of AlN precipitation and temperature during solidification process

下载: 全尺寸图片幻灯片

3.3 实际结果验证

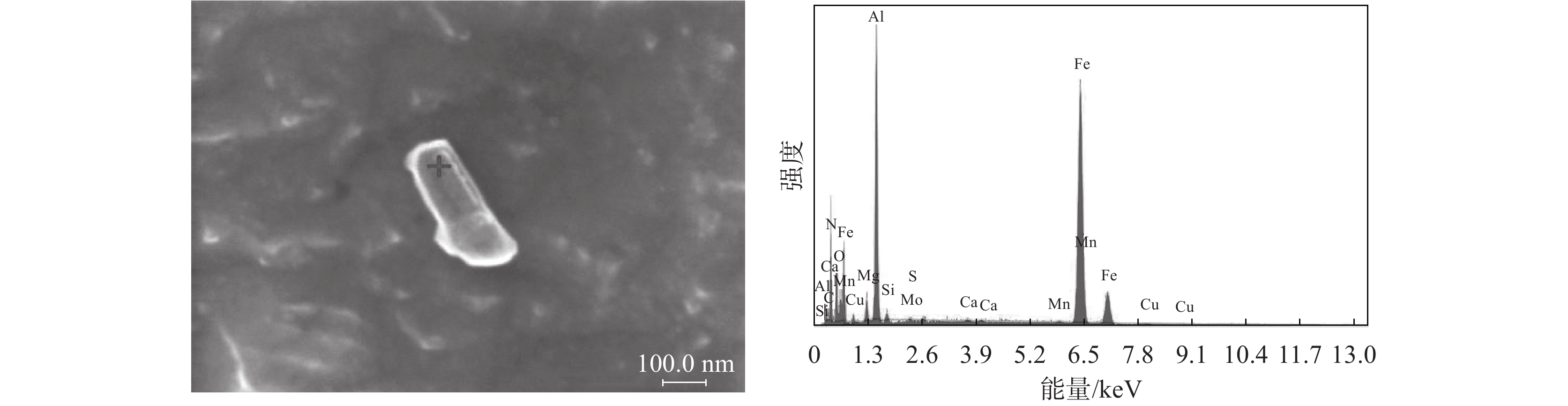
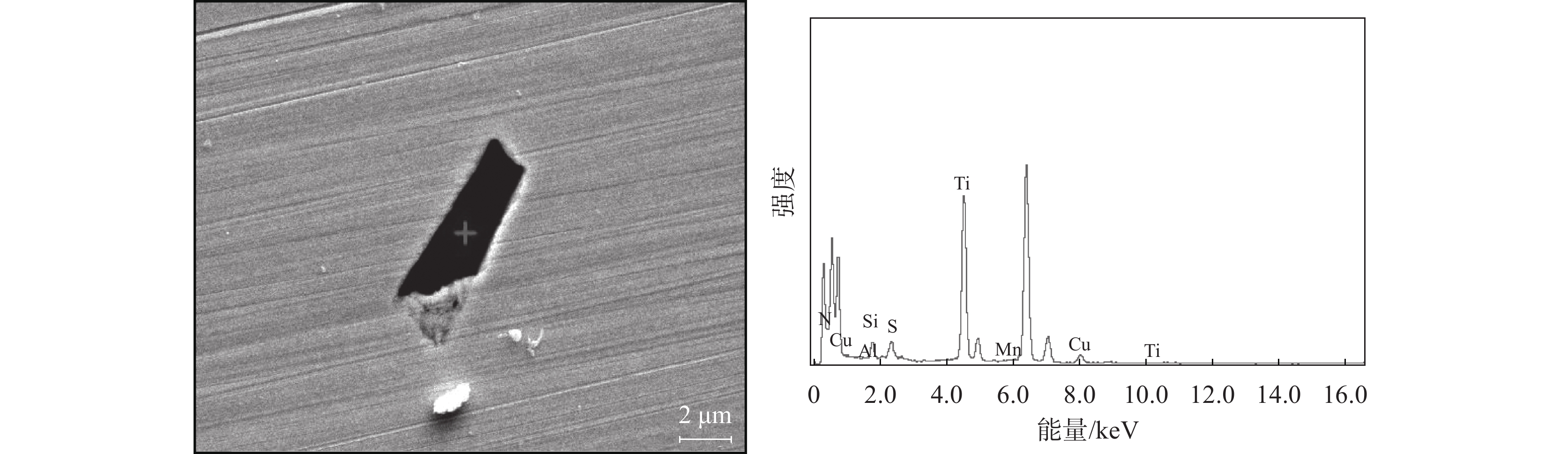
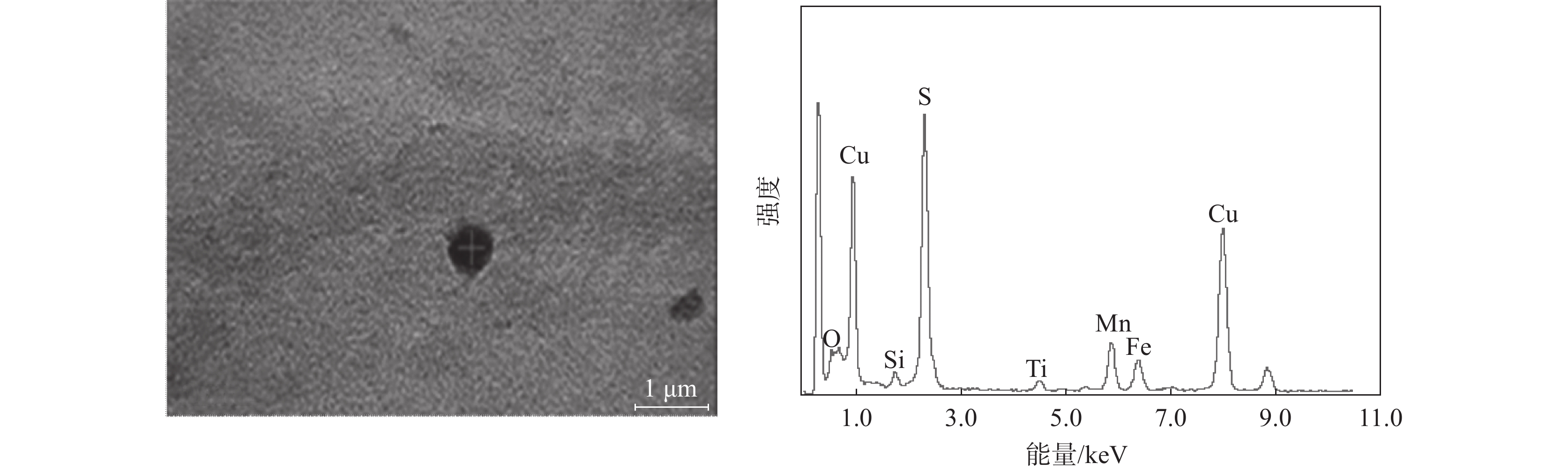
为了证明上述分析的准确性，仅从热轧板取试样，经过电解抛光，并在扫描电镜下观察。图14～17为实际检测到的结果。这也说明了上述分析的可行性。

图 11 凝固过程中TiN析出溶度积关系

Figure 11. Relationship of solubility product of TiN precipitation and temperature during solidification process

下载: 全尺寸图片幻灯片

图 12 凝固过程中MnS析出溶度积关系

Figure 12. Relationship of solubility product of MnS precipitation and temperature during solidification process

下载: 全尺寸图片幻灯片

图 13 凝固过程中Cu₂S析出溶度积关系

Figure 13. Relationship of solubility product of Cu₂S precipitation and temperature during solidification process

下载: 全尺寸图片幻灯片

图 14 扫描电镜下的AlN析出物

Figure 14. SEM photos of AlN precipitates

下载: 全尺寸图片幻灯片

图 15 扫描电镜下的TiN析出物

Figure 15. SEM photos of TiN precipitates

下载: 全尺寸图片幻灯片

图 16 扫描电镜下的MnS析出物

Figure 16. SEM photos of MnS precipitates

下载: 全尺寸图片幻灯片

图 17 扫描电镜下的Cu₂S析出物

Figure 17. SEM photos of Cu₂S precipitates

下载: 全尺寸图片幻灯片

4. 结论

1）在钢液中即液相线温度以上，AlN、TiN、MnS和Cu₂S均不能析出；

2）在凝固过程中即液相线温度以下，AlN在L→α阶段以及固相线以下部分温度段析出，即1700～1788 K温度区间可能析出，TiN在L→α阶段以及固相线以下部分温度段析出，即1588～1788 K温度区间析出，MnS仅在L→α阶段，即1768～1788 K温度区间析出，Cu₂S在固相线以下部分温度段，即1420～1768 K温度区间时析出。

图 1 950 ℃ GH3128蠕变时间曲线^[13]

Figure 1. Creep time curve of GH3128 at 950 ℃^[13]

下载: 全尺寸图片幻灯片

图 2 蠕变损伤模拟曲线

Figure 2. Creep damage simulation curves

下载: 全尺寸图片幻灯片

图 3 ABAQUS子程序流程

Figure 3. ABAQUS subroutine flow

下载: 全尺寸图片幻灯片

图 4 试验数据与Sinh蠕变模型模拟结果

Figure 4. Experimental data and simulation results of the Sinh creep model

下载: 全尺寸图片幻灯片

表 1 三种损伤模型方程参数

Table 1. Equation parameters of the three damage models

模型	参数
K-R模型	$ A $：4.36 e^-15；$ {n}_{1} $：4.71；$ {M}_{1} $：4.38 e^-14；$ \varnothing $：15.01；$ {\chi }_{1} $：4.31
Liu-M模型	$ C $：4.36 e^-15；$ {n}_{2} $：4.71；$ {M}_{3} $：6.02 e^-13；$ p $：4.31；$ q $：4.32
Sinh模型	$ {\rm B} $：1.34 e^-7；$ {\mathrm{\sigma }}_{\mathrm{s}} $：19.41；$ {\sigma }_{t} $：22.80； $ {M}_{2} $：6.15 e^-6；$ \phi $：4.50；λ：2.50；$ {\chi }_{2} $：1

下载: 导出CSV

表 2 模型蠕变寿命预测及误差对比

Table 2. Comparison of creep life prediction and errors of the models

应力/ MPa	试验寿命/s	K-R模型		Sinh模型		Liu-M模型
应力/ MPa	试验寿命/s	蠕变寿命/s	误差/%	蠕变寿命/s	误差/%	蠕变寿命/s	误差/%
100	3696.8	3914.5	5.9	4049.7	9.5	3984.7	7.8
90	6917.5	6164.4	10.8	6322.11	8.6	6275.0	9.3
80	9721.0	10241.5	5.2	9742.7	0.2	10425.2	7.2

下载: 导出CSV

参考文献(16)

[1]	LIU T Y, LAI Y, FU J H, et al. High temperature rheological behavior and microstructure evolution of GH3128 alloy[J]. Metal Heat Treatment, 2020,45(6):141-148. (刘庭耀, 赖宇, 付建辉, 等. GH3128合金的高温流变行为与组织演变规律[J]. 金属热处理, 2020,45(6):141-148. LIU T Y, LAI Y, FU J H, et al. High temperature rheological behavior and microstructure evolution of GH3128 alloy[J]. Metal Heat Treatment, 2020, 45（6）: 141-148.
[2]	YANG B, WU S H, BAO Z N, et al. Thermal deformation behavior and phenomenological constitutive model of GH3128 alloy[J]. Forging Technology, 2022,47(5):226-234. (杨波, 吴诗豪, 包振男, 等. GH3128合金热变形行为与唯象本构模型[J]. 锻压技术, 2022,47(5):226-234. YANG B, WU S H, BAO Z N, et al. Thermal deformation behavior and phenomenological constitutive model of GH3128 alloy[J]. Forging Technology, 2022, 47（5）: 226-234.
[3]	YUAN Z F, JIANG J, CHENG Z W, et al. Study on high temperature mechanical properties of fiber laser GH3128 lap joint[J]. China Laser, 2022,49(21):170-178. (袁振飞, 蒋劲, 程智伟, 等. 光纤激光GH3128搭接接头高温力学性能研究[J]. 中国激光, 2022,49(21):170-178. YUAN Z F, JIANG J, CHENG Z W, et al. Study on high temperature mechanical properties of fiber laser GH3128 lap joint[J]. China Laser, 2022, 49（21）: 170-178.
[4]	AN F P, LIU X W, ZHANG L J, et al. Dramatic improvement of the strength of laser welded joints of Nb521 to GH3128 by adding pure copper as an interlayer[J]. International Journal of Refractory Metals and Hard Materials, 2023,116:106367. doi: 10.1016/j.ijrmhm.2023.106367
[5]	XU G, PENG L D, JIN H W. Creep damage characteristics and constitutive model of water-bearing coal[J]. Mining Research and Development, 2023,43(9):152-157. (徐刚, 彭来栋, 金洪伟. 含水煤体蠕变损伤特性及本构模型研究[J]. 矿业研究与开发, 2023,43(9):152-157. XU G, PENG L D, JIN H W. Creep damage characteristics and constitutive model of water-bearing coal[J]. Mining Research and Development, 2023, 43（9）: 152-157.
[6]	PAN X K, ZHOU X P, ZOU Y Y, et al. Creep mechanical properties and creep damage model of sandstone considering temperature effect based on acoustic emission[J]. Fatigue Fracture of Engineering Materials Structures, 2023,47(1):35-55.
[7]	MAO X P, GUO Q, ZHANG S Y, et al. Experimental study on creep damage of nickel-based alloy C276[J]. Nuclear Power Engineering, 2013,34(2):86-89. (毛雪平, 郭琦, 张声远, 等. 镍基合金C276蠕变损伤的实验研究[J]. 核动力工程, 2013,34(2):86-89. doi: 10.3969/j.issn.0258-0926.2013.02.020 MAO X P, GUO Q, ZHANG S Y, et al. Experimental study on creep damage of nickel-based alloy C276[J]. Nuclear Power Engineering, 2013, 34（2）: 86-89. doi: 10.3969/j.issn.0258-0926.2013.02.020
[8]	STEWART C M, GORDON A P. Strain and damage-based analytical methods to determine the Kachanov–Rabotnov tertiary creep-damage constants[J]. International Journal of Damage Mechanics, 2012,21(8):1186-1201. doi: 10.1177/1056789511430519
[9]	HAQUE M S, STEWART C M. Finite element analysis of waspaloy using sinh creep-damage constitutive model under triaxial stress state[J]. Journal of Pressure Vessel Technology, 2016,138(3):031408. doi: 10.1115/1.4032704
[10]	ZHANGN Q, LIU X B, ZHU L, et al. Comparison of creep damage models based on P91 steel[J]. Journal of Northwest University: Natural Science, 2017,47(5):711-716. (张琦, 刘新宝, 朱麟, 等. 基于P91钢的蠕变损伤模型比较[J]. 西北大学学报: 自然科学版, 2017,47(5):711-716. ZHANGN Q, LIU X B, ZHU L, et al. Comparison of creep damage models based on P91 steel[J]. Journal of Northwest University: Natural Science, 2017, 47（5）: 711-716.
[11]	MURAKAMI S, LIU Y, MIZUO M. Computational methods for creep fracture analysis by damage mechanics[J]. Compute methods in applied mechanics and engineering, 2000,183(1-2):15-33. doi: 10.1016/S0045-7825(99)00209-1
[12]	ZHAO L. Study on creep damage mechanism of P92 steel welded joints[D]. Tianjin: Tianjin University, 2009. (赵雷. P92钢焊接接头的蠕变损伤机理研究[D]. 天津:天津大学, 2009. ZHAO L. Study on creep damage mechanism of P92 steel welded joints[D]. Tianjin: Tianjin University, 2009.
[13]	XU D F. Study on creep characteristics of cooling tube of GH3128 superalloy intermediate heat exchanger[D]. Qinhuangdao: Yanshan University, 2019. (徐殿峰. GH3128高温合金中间换热器冷却管蠕变特性研究[D]. 秦皇岛:燕山大学, 2019. XU D F. Study on creep characteristics of cooling tube of GH3128 superalloy intermediate heat exchanger[D]. Qinhuangdao: Yanshan University, 2019.
[14]	KACHANOV L M. Rupture time under creep conditions[J]. International Journal of Fracture, 1999,97(1):11-18.
[15]	RABOTNOV Y N, LECKIE F A, PRAGERW W. Creep problems in structural members[J]. Journal of Applied Mechanics, 1970,37(1):249.
[16]	CHEN X, ZHOU G Y, TU S D. Finite element analysis of creep crack propagation of T-brazed joint[J]. Mechanical Strength, 2014,36(5):790-796. (陈兴, 周帼彦, 涂善东. T型钎焊接头蠕变裂纹扩展的有限元分析[J]. 机械强度, 2014,36(5):790-796. CHEN X, ZHOU G Y, TU S D. Finite element analysis of creep crack propagation of T-brazed joint[J]. Mechanical Strength, 2014, 36（5）: 790-796.

施引文献

资源附件(0)

访问统计

点击查看大图

图(4) / 表(2)

计量

文章访问数: 31
HTML全文浏览量: 18
PDF下载量: 4
被引次数: 0

0. 引言
1. 热力学计算推导
2. 热力学计算条件
3. 热力学计算结果
3.1 液相计算结果
3.2 凝固过程分析
3.3 实际结果验证
4. 结论

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

GH3128蠕变损伤模型预测以及有限元模拟

doi: 10.7513/j.issn.1004-7638.2025.01.023

作者简介:
康晓东，1998年出生，男，山西大同人，硕士，研究方向：金属材料的力学性能，E-mail：kxdkyb05@126.com

计量