Creep damage model prediction and finite element simulation of GH3128
-
摘要: 从蠕变损伤方程构建和有限元模拟两方面对GH3128合金在950 ℃条件下的高温蠕变行为进行分析。首先,结合K-R模型、Sinh模型及Liu-M模型进行蠕变损伤方程构建,继而对模型寿命预测和损伤行为进行对比分析,发现应力100、90 MPa和80 MPa下寿命预测相对误差最大仅为10.8%,累积相对误差Sinh模型最小为18.3%。而对损伤行为的对比发现Sinh模型和Liu-M模型较K-R模型损伤演化过程要缓和,有利于在有限元模拟时网格的划分,由此得出:对GH3128合金蠕变行为预测效果最好的是Sinh模型。最后,利用ABAQUS软件中Creep子程序接口,通过二次开发编写Sinh模型,有限元模拟的结果表明Sinh模型对GH3128合金蠕变行为分析较为准确和高效。Abstract: Creep damage equation construction and finite element simulation were used to analyze the high temperature creep behavior of GH3128 alloy at 950 ℃. Firstly, the creep damage equation was constructed by combining the K-R model, the Sinh model and the Liu-M model. Then the life prediction and damage behavior of the model were compared and analyzed. It is found that the maximum relative error of life prediction under 100, 90 MPa and 80 MPa is only 10.8%. The cumulative relative error of the Sinh model was the smallest with the value of 18.3%. The comparison of damage behaviors shows that the damage evolution processes of the Sinh model and the Liu-M model are slower than that of the K-R model, which is beneficial to the meshing in finite element simulation. Therefore, it is concluded that the Sinh model has the best prediction effect on the creep behavior of GH3128 alloy. Finally, the Creep subroutine interface in ABAQUS software was used to program the Sinh model through secondary development. The results of finite element simulation showed that the Sinh model was relatively accurate and efficient in analyzing the creep behavior of GH3128 alloy.
-
Key words:
- damage model /
- Creep of the material /
- Secondary development /
- ABAQUS software
-
0. 引言
GH3128合金具有高的塑性、良好的抗氧化性、较高的持久蠕变强度以及较好的抗腐蚀和焊接性能,该合金主要用于950 ℃下长期工作的燃烧室火焰筒、加力燃烧室壳体等高温零部件[1−4]。由于该材料服役温度可达950 ℃,在这样的高温环境中工作,材料往往会发生蠕变损伤甚至会断裂,影响构件的正常工作,因此精准预测GH3128合金950 ℃下的蠕变损伤行为是极为重要的。
徐刚等[5]、PAN 等[6]采用以损伤力学为基础的蠕变损伤模型模拟材料高温环境中的蠕变行为开展了大量工作。毛雪平[7]根据C276在650、700 、750 ℃下不同应力的蠕变数据,采用θ外推法、Kachanov方程和Norton方程对数据进行计算,结果表明使用Kachanov方程计算得到的损伤因子趋于一致,且较之于Norton方程计算得到的损伤因子偏保守,并且θ外推法拟合得到的蠕变曲线与试验曲线重合度较高。STEWART等[8]构建出一种基于应变和损伤的方法来确定材料的三阶段蠕变常数,并通过Waspaloy镍基合金700 ℃的蠕变数据构建Kachanov Rabotnov方程,与试验数据对比,结果证明该方法用于预测材料蠕变行为是准确及高效的。HAQUE等[9]采用K-R蠕变模型和Sinh蠕变模型模拟了Waspaloy合金700 ℃不同应力水平下的蠕变和损伤演化特性,发现Sinh模型较K-R蠕变模型能够较为准确地预测不同条件下的蠕变变形和断裂寿命。Sinh模型以及Liu-M蠕变损伤模型在描述蠕变损伤行为时可获得更为精准的结果。
在现有的蠕变损伤模型的基础上结合有限元方法,针对材料的蠕变特性进行研究已成为当前蠕变研究的一个重要方面。张琦[10]基于P91钢580 ℃和620 ℃在不同应力条件下高温蠕变试验结果,构建了P91钢的双曲正弦蠕变损伤模型,利用ABAQUS有限元软件的UMAT子程序接口,对双曲正弦本构模型进行二次开发,模拟分析其蠕变行为,结果表明模拟和试验曲线重合度较高。MURAKAMI等[11]通过对带裂纹平板进行有限元分析,发现传统K-R损伤方程有限元分析存在一定应力敏感性问题,从而导致数值结果对网格的依赖性。为了抑制这种奇异应力敏感性的关键阶段的损伤,设计出一种新的蠕变损伤模型,使用设计的模型能够避免在分析过程中发生应力敏感问题。赵雷[12]采用改进Kachanov-Rabotnov(K-R)损伤模型,并编制了该模型的UMAT用户子程序,后续使用子程序对单轴蠕变在650 ℃下70 MPa的条件进行有限元模拟,有限元计算曲线和试验蠕变曲线拟合良好,结果表明改进的损伤模型具有较高的可靠性。
基于GH3128合金950 ℃的蠕变试验数据,比较K-R模型、Sinh模型和Liu-M模型的预测能力。基于模拟结果,利用ABAQUS软件对Sinh模型进行有限元二次开发,验证Sinh模型的有效性。结果可为GH3128合金高温蠕变行为预测提供理论基础。
1. 试验结果
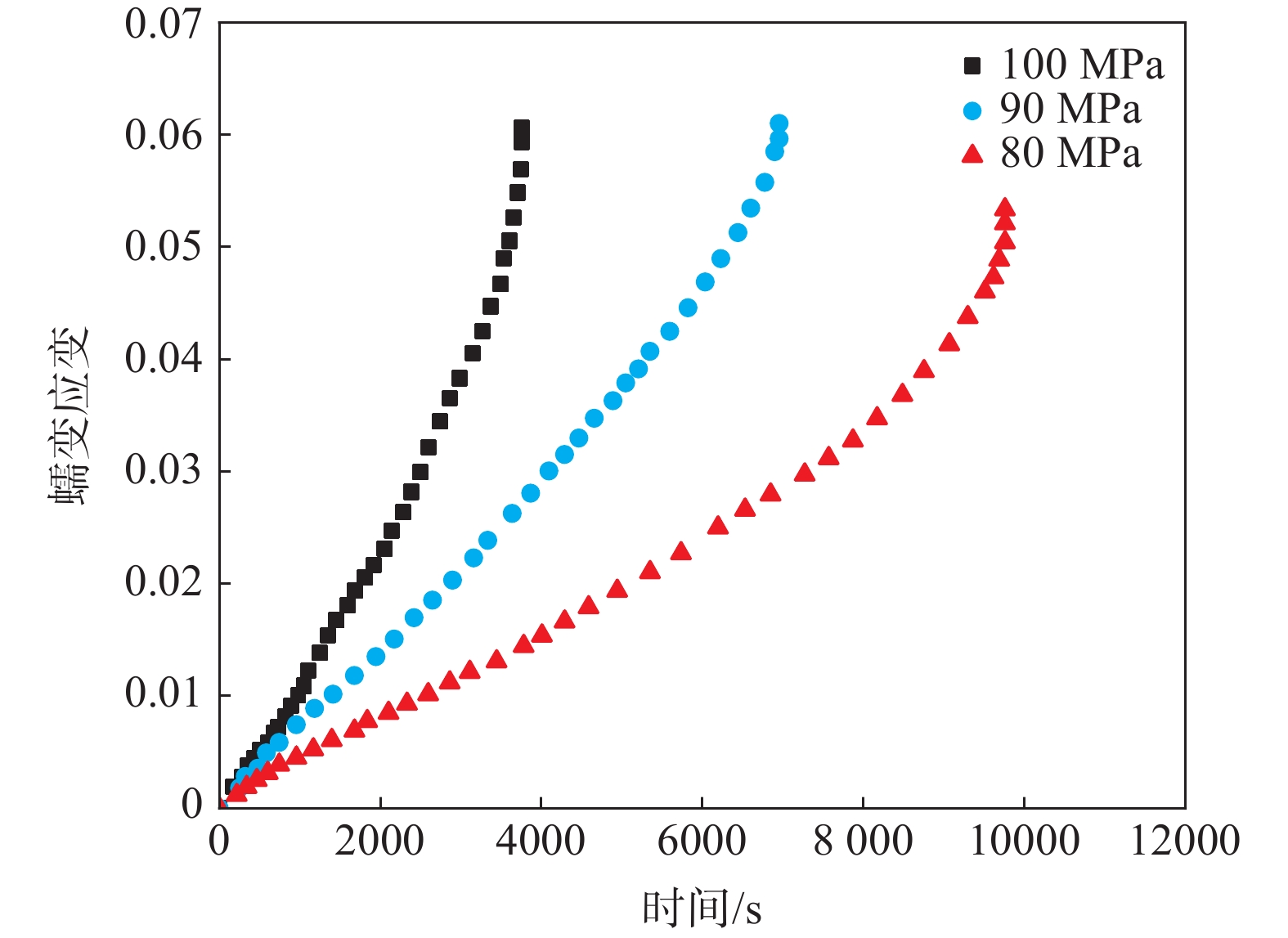
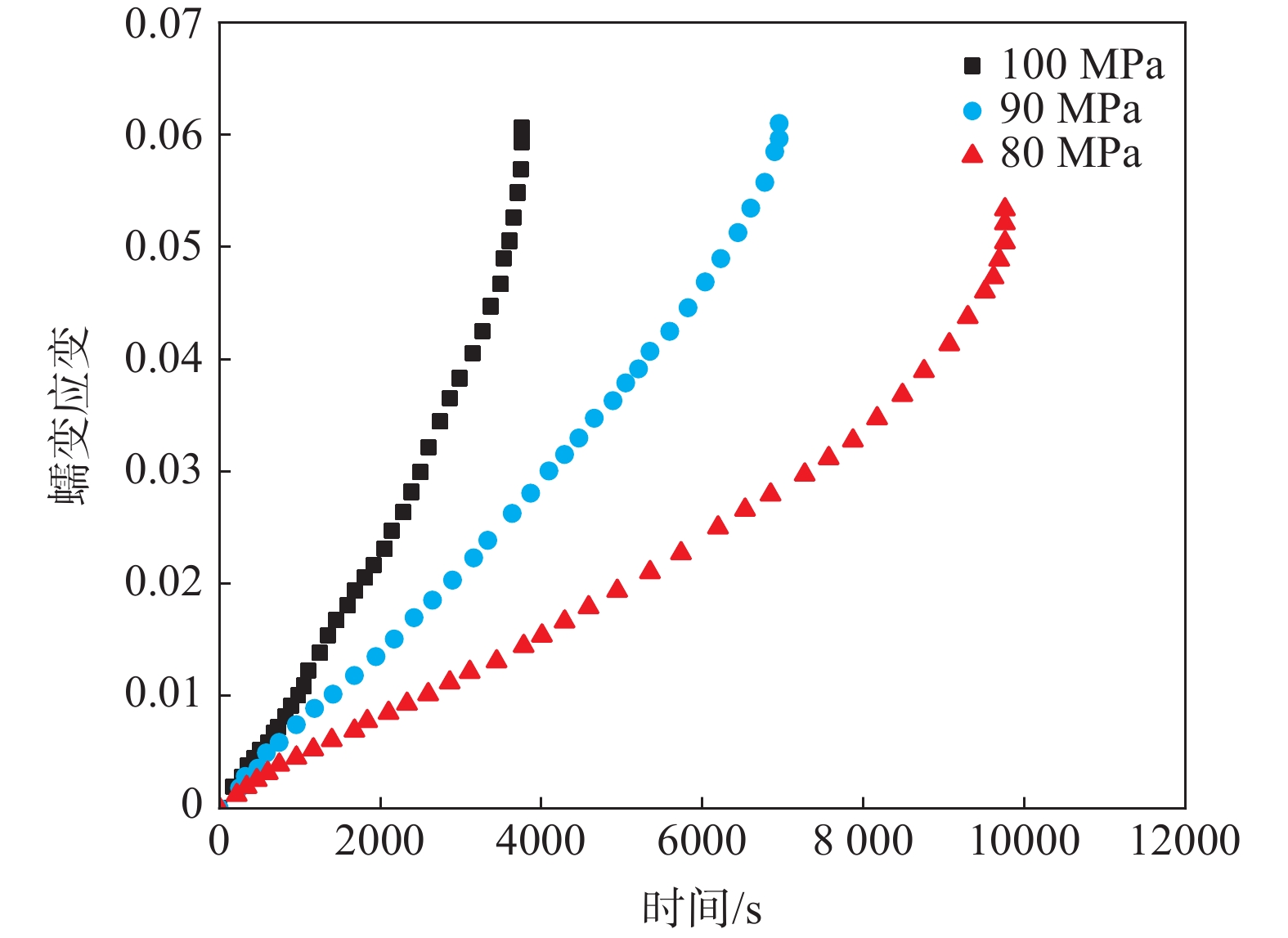
GH3128合金的蠕变试验数据取自文献[13]。试样为直径10 mm,长度120 mm的圆棒试样,进行了950 ℃下,应力水平分别为80、90 MPa和100 MPa下的蠕变试验,具体试验结果如图1所示。
2. 损伤模型
2.1 K-R损伤模型
经典地描述蠕变过程中损伤变量$ D $与应力$ \sigma $关系的模型是K-R蠕变损伤模型[14−15],见式(1)~(7)。
$$ {\dot{\varepsilon }}_{c}=A{\left(\frac{\sigma }{1-D}\right)}^{{n}_{1}} $$ (1) $$ \dot{D}=\frac{{M}_{1}{\sigma }^{{\boldsymbol{\chi }}_{1}}}{{\left(1-D\right)}^{\varnothing }} $$ (2) 式中 $ A $,$ {n}_{1} $为第二阶段蠕变常数;$ \sigma $为应力;$ D $为损伤变量;$ {M}_{1} $、$ \mathrm{\varnothing } $、$ {\chi }_{1} $为第三阶段材料常数,$ {\chi }_{1}\geqslant 1 $。随后对式(2)进行数值积分后就获得了材料的损伤演化方程:
$$ D\left(t\right)=1-(1-t/t\mathrm{_r})^{\frac{1}{\varnothing+1}} $$ (3) $$ t\mathrm{_r}=\frac{1}{(\varnothing+1)M_1\sigma^{\chi_1}} $$ (4) 式中:$ t\mathrm{_r} $是蠕变断裂时间。通过式(4)拟合后得到了蠕变第三阶段参数$ {M}_{1} $、$ {\chi }_{1} $。将式(3)代入式(2)后积分得到以下公式:
$$ \varepsilon_c\left(t\right)=\frac{A\sigma^{n_1}t\mathrm{_r}}{1-n_1/(1+\varnothing)}[1-(1-t/t\mathrm{_r})^{1-n_1/(1+\varnothing)}] $$ (5) 当时间为蠕变寿命$ t\mathrm{_r} $时,可以得到蠕变破断应变为:
$$ \varepsilon_r\left(t\right)=\frac{A\sigma^{n_1}t\mathrm{_r}}{1-n_1/(1+\varnothing)} $$ (6) 联立式(5)和式(6)得:
$$ \xi =1-{(1-\eta )}^{\Delta } $$ (7) 式中:$ \xi=\varepsilon/\varepsilon\mathrm{_r} $;$ \eta=t/t\mathrm{_r} $;$ \Delta =1-{n}_{1}/(1+\mathrm{\varnothing }) $。应用式(7)对图像进行拟合后得到方程参数$ \mathrm{\varnothing } $。
2.2 Sinh损伤模型
因为该模型含有双曲正弦函数,因此被称为Sinh模型[9]。该模型表示如式(8)~(13)所示。
$$ \dot{\varepsilon_c}=\rm{B}\mathrm{\boldsymbol{sin}h}\left(\frac{\sigma}{\sigma_s}\right)\mathrm{exp}\left(\lambda D^{\tfrac{3}{2}}\right) $$ (8) $$ \dot{D}=\frac{{M}_{2}(1-\exp(-\varphi \left)\right)}{\varphi }{\sin}{\mathrm{h}}{\left(\frac{\sigma }{{\sigma }_{t}}\right)}^{{\chi }_{2}}\exp\left(\varphi D\right) $$ (9) 式中:$ {\rm B} $和$ {\sigma }_{s} $是第二阶段蠕变常数,$ {M}_{2} $,$ {\sigma }_{t} $为双曲正弦模型常数,$ \varphi $,$ {\chi }_{2} $为第三阶段蠕变损伤常数。$ \mathrm{\lambda }=\mathrm{l}\mathrm{n}\left(\dfrac{{\dot{\varepsilon }}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}{{\dot{\varepsilon }}_{\mathrm{m}\mathrm{i}\mathrm{n}}}\right) $。对应的稳态阶段的蠕变方程为:
$$ \dot{\varepsilon}_c=B\mathrm{sinh}\left(\frac{\sigma}{\sigma_S}\right) $$ (10) 由(11)拟合得到$ {\mathrm{\sigma }}_{\mathrm{s}} $及$ {\rm B} $。将式(9)重新整理:
$$ D\left(\dot{\varepsilon}_c\right)=\frac{1}{\lambda}\mathrm{ln}\left(\frac{\dot{\varepsilon}_c\left(t\right)}{B\mathrm{sinh}\left(\dfrac{\sigma}{\sigma_S}\right)}\right)^{\tfrac{2}{3}} $$ (11) 对式(12)进行积分:
$$ D\left(t\right)=-\frac{1}{\phi}\mathrm{l}\mathrm{n}\left(1-\left(1-\mathrm{e}\mathrm{x}\mathrm{p}(-\phi)\right)\frac{t}{t\mathrm{_r}}\right) $$ (12) $$ t\mathrm{_r}=\left(M_2\mathrm{sinh}\left(\frac{\sigma}{\sigma_t}\right)^{\chi_2}\right)^{-1} $$ (13) $ {M}_{2} $、$ {\sigma }_{t} $可以通过式(14)结合试验数据拟合得出。$ \phi $由式(13)求得。
2.3 Liu-M损伤模型
经典的Liu-M模型[9]表述如式(14)~(18)所示。
$$ \dot{\varepsilon_c}=C\sigma^{n_2}\mathrm{exp}\left(\dfrac{2(n_2+1)}{\pi\sqrt{1+\dfrac{3}{n_2}}}D^{\tfrac{3}{2}}\right) $$ (14) $$ \dot{D}=\frac{M_3(1-\mathrm{e}^{-q})}{q}\sigma^p\mathrm{e}^{qD} $$ (15) 式中:$ C $和$ {n}_{2} $是第二阶段蠕变常数,由K-R模型已求得,$ {M}_{3} $,$ p $为模型常数,$ q $为第三阶段蠕变损伤常数。对式(15)分离变量并积分,且断裂时断裂时间和应力之间的关系式为:
$$ t\mathrm{_r}=\frac{\sigma^{-p}}{M_3} $$ (16) 由式(16)根据断裂数据拟合材料常数$ {M}_{3} $、$ p $。在初始时刻时可得到蠕变损伤变量与时间的数学关系:
$$ D\left(t\right)=-\frac{{\mathrm{ln}}(1-{M}_{3}(1-{{\mathrm{e}}}^{-q}\left){\sigma }^{p}t\right)}{q} $$ (17) 将式(17)代入式(14),得到了蠕变应变率的表达:
$$ {\dot{{\varepsilon }_{cr}}=C{\sigma }^{{n}_{2}}\exp\left(\dfrac{2\left({n}_{2}+1\right)}{\pi \sqrt{1+\dfrac{3}{{n}_{2}}}}{\left(-\dfrac{\mathrm{ln}\left(1-{M}_{3}\left(1-{{\mathrm{e}}}^{-q}\right){\sigma }^{p}t\right)}{q}\right)}^{\tfrac{3}{2}}\right)} $$ (18) 通过式(18)计算得到$ q $值。表1所示为模型方程参数。
表 1 三种损伤模型方程参数Table 1. Equation parameters of the three damage models模型 参数 K-R模型 $ A $:4.36 e-15;$ {n}_{1} $:4.71;$ {M}_{1} $:4.38 e-14;$ \varnothing $:15.01;$ {\chi }_{1} $:4.31 Liu-M模型 $ C $:4.36 e-15;$ {n}_{2} $:4.71;$ {M}_{3} $:6.02 e-13;$ p $:4.31;$ q $:4.32 Sinh模型 $ {\rm B} $:1.34 e-7;$ {\mathrm{\sigma }}_{\mathrm{s}} $:19.41;$ {\sigma }_{t} $:22.80;
$ {M}_{2} $:6.15 e-6;$ \phi $:4.50;λ:2.50;$ {\chi }_{2} $:13. 模型结果与比较
3.1 模型蠕变寿命比较
采用K-R模型、Sinh模型和Liu-M模型的计算得到不同应力条件下材料的蠕变寿命,结果见表2所示,与试验数据比较结果亦列于表2。
表 2 模型蠕变寿命预测及误差对比Table 2. Comparison of creep life prediction and errors of the models应力/
MPa试验
寿命/sK-R模型 Sinh模型 Liu-M模型 蠕变
寿命/s误差/% 蠕变
寿命/s误差/% 蠕变
寿命/s误差/% 100 3696.8 3914.5 5.9 4049.7 9.5 3984.7 7.8 90 6917.5 6164.4 10.8 6322.11 8.6 6275.0 9.3 80 9721.0 10241.5 5.2 9742.7 0.2 10425.2 7.2 在工程应用中,模拟值与试验值的相对误差在20%以内认为可以接受,通过表2误差对比可以得出,模型预测蠕变断裂时间的相对误差最大仅为10.8%,说明三个模型寿命预测较为准确。应力为100 MPa时蠕变断裂时间误差最大的是Sinh模型,最小的为K-R模型;在应力为90 MPa下,蠕变断裂时间误差最大的为K-R模型,最小的为Sinh模型;在应力为80 MPa下蠕变断裂时间误差最大的是Liu-M模型,最小的为Sinh模型;综合三种应力条件下累计误差Sinh模型最小,为18.3%。
3.2 蠕变损伤演化模型对比
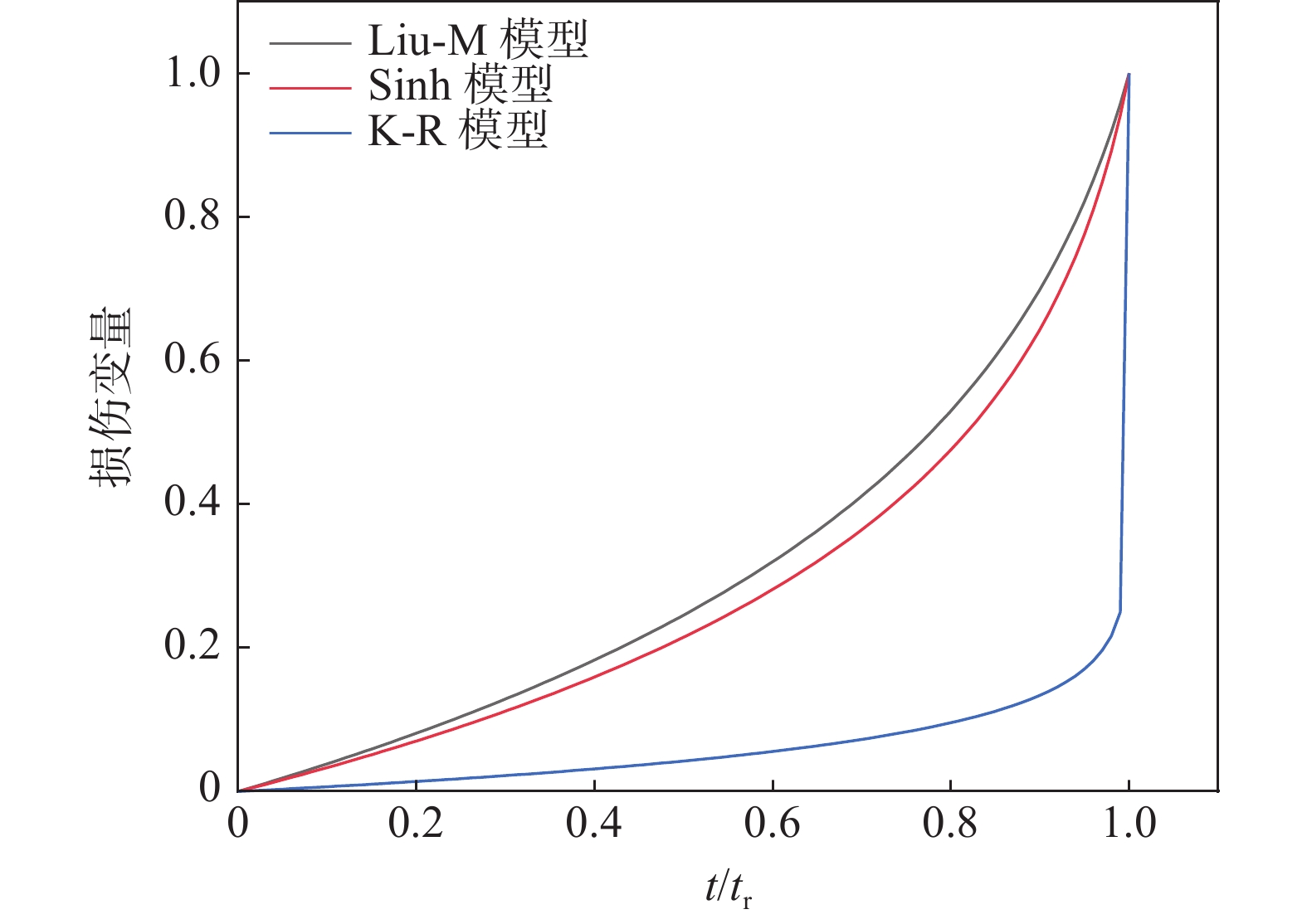
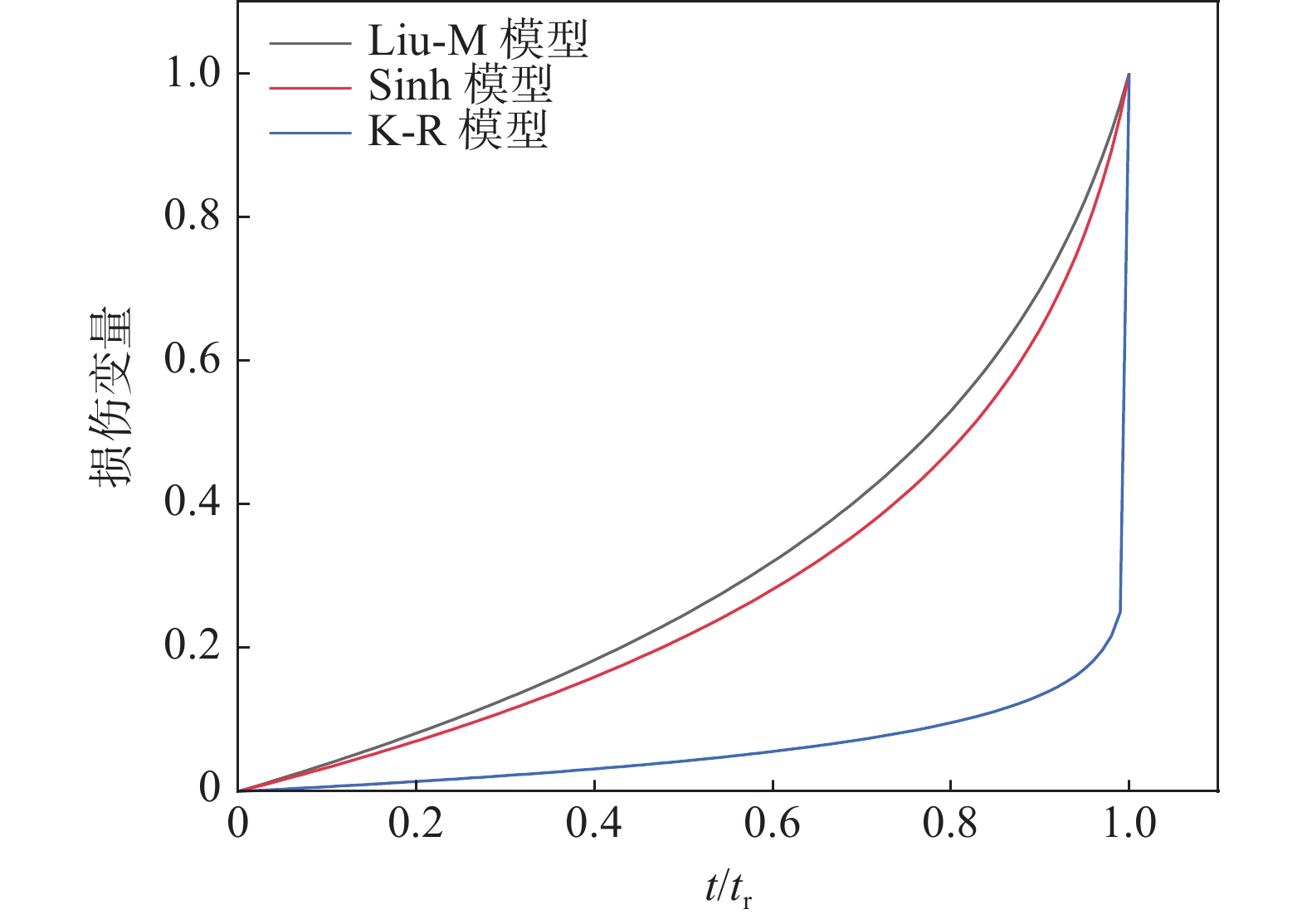
通过式(4)(12)(17)计算损伤变量D可以用来分析三种模型的损伤演化,结果如图2所示。
由图2可知,同一时刻,K-R模型损伤变量要比Sinh模型和Liu-M模型损伤更低,而K-R模型损伤变量在蠕变中后期发生了突变,损伤变量D在很短的时间内就达到了1;而Sinh模型和Li-M模型较K-R模型损伤演化过程要缓和。通过模型损伤演化方程对比发现,各个模型损伤变化由其损伤参数控制,但K-R模型损伤方程会使曲线后期产生突变的情况,这种特性不利于在有限元模拟中网格的划分,而Sinh模型和Liu-M模型可以有效地缓解这种问题。
4. 蠕变损伤的数值模拟
4.1 ABAQUS子程序
ABAQUS并不提供上述蠕变损伤模型,但为用户提供了多种形式的子程序接口,能够将用户自己的本构方程嵌入到ABAQUS中。其中Creep子程序可以定义蠕变应变相关的粘弹性、粘塑性和蠕变行为,并使用自己的蠕变本构方程来定义蠕变曲线。首先使用Fortran语言来编译损伤模型,然后在ABAQUS的Property模块定义材料蠕变属性时选择用户自定义,最后通过ABAQUS的Job模块,在提交任务时调用Creep子程序来进行有限元模拟。
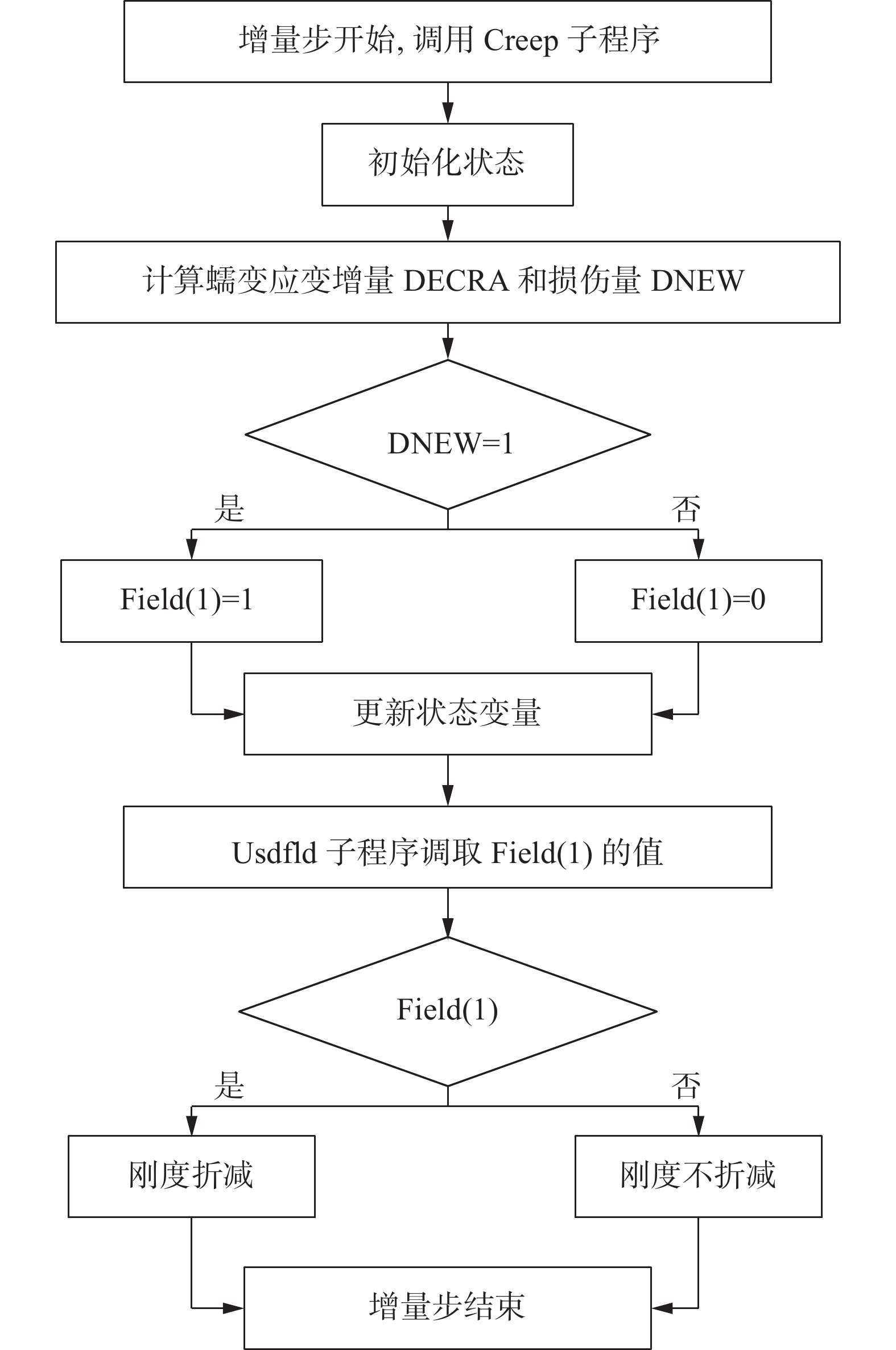
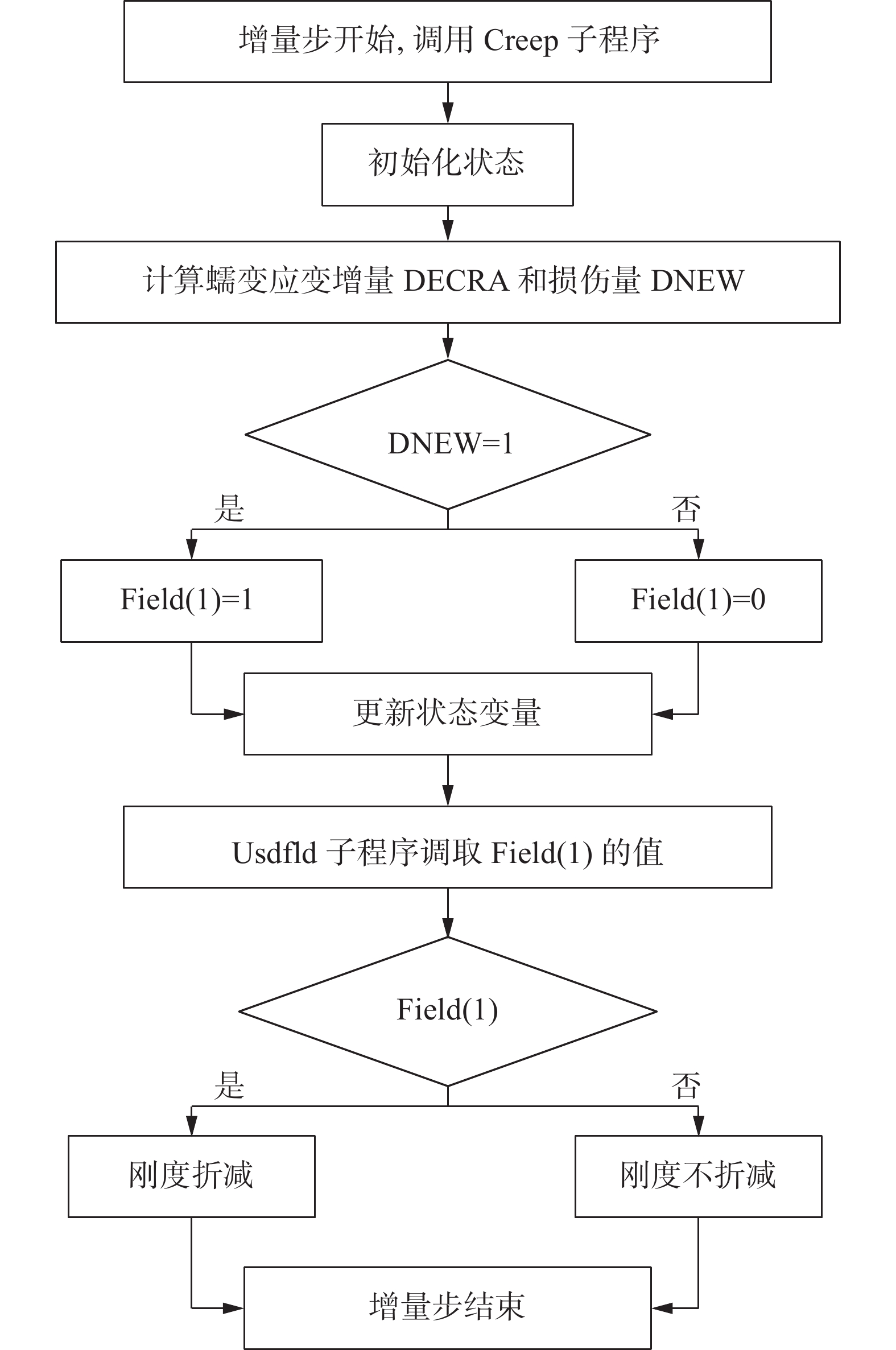
由模型比较的结果可知,Sinh模型的相对误差最小,故选择Sinh模型来对GH3128合金进行有限元模拟,建立基于Sinh蠕变损伤模型的Creep子程序以及Usdfld子程序来对损伤量达到1的材料单元进行刚度折减。首先,根据式(8)(9)分别计算GH3128合金的蠕变应变增量和损伤增量,在材料单元的损伤变量大于1时,则将该单元的刚度折减为1,并对此单元上的积分点的刚度进行折减;否则,刚度折减为0[16],直至增量步结束。整个子程序流程如图3所示。
4.2 有限元模拟
在有限元模拟过程中,一般想要降低有限元计算的难度,可以忽略掉端部几何形状(螺纹)的影响,并且由于圆棒形试样的轴对称形状,可以选取试样的1/4试样进行三维建模。采用C3D8R单元进行模拟计算,共得到
7575 个节点,6000 个单元。在模型的轴向和径向中面上采用对称约束,在模型的端部分别施加80、90 MPa和100 MPa的载荷。4.3 有限元模拟结果及分析
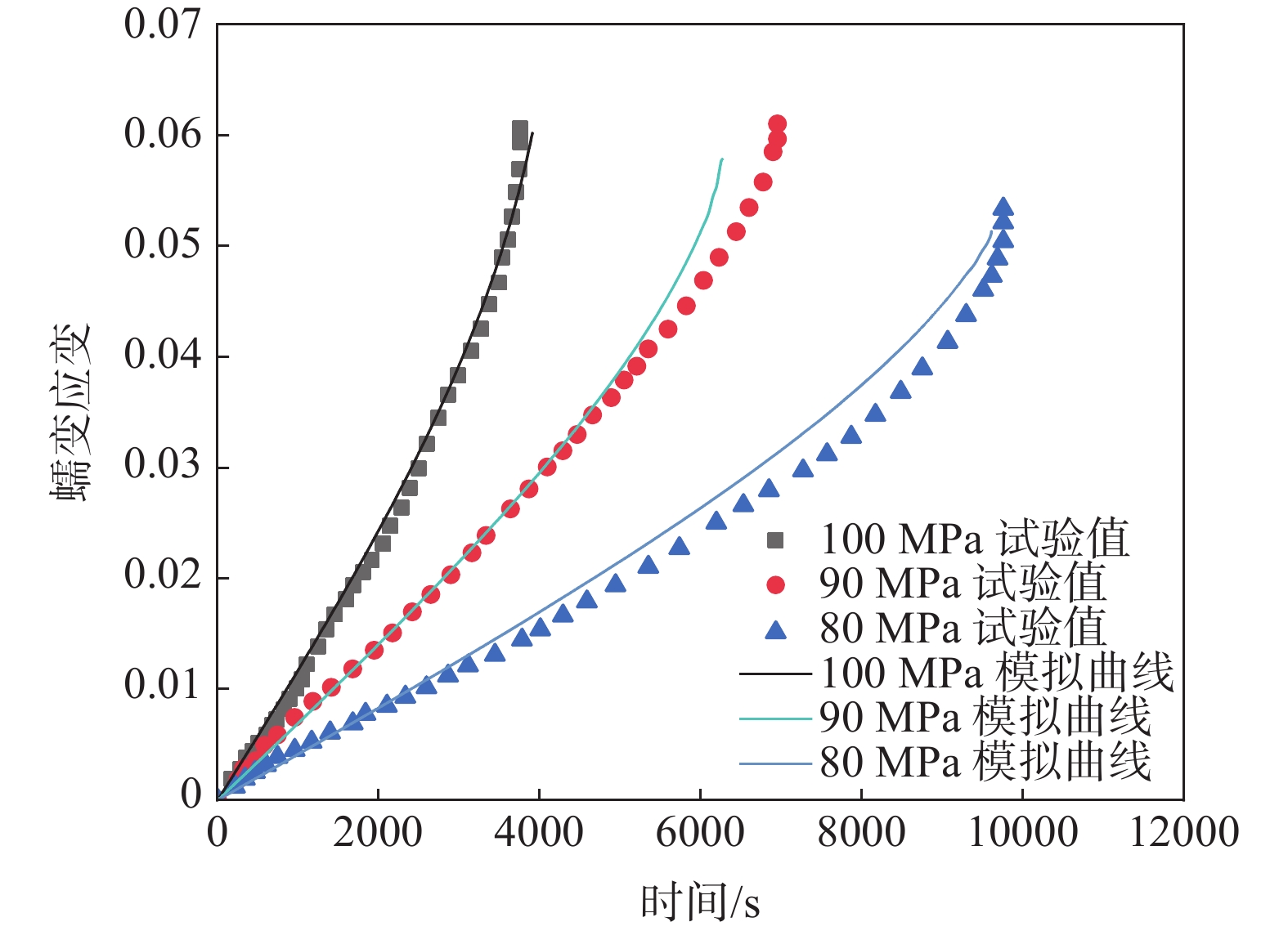
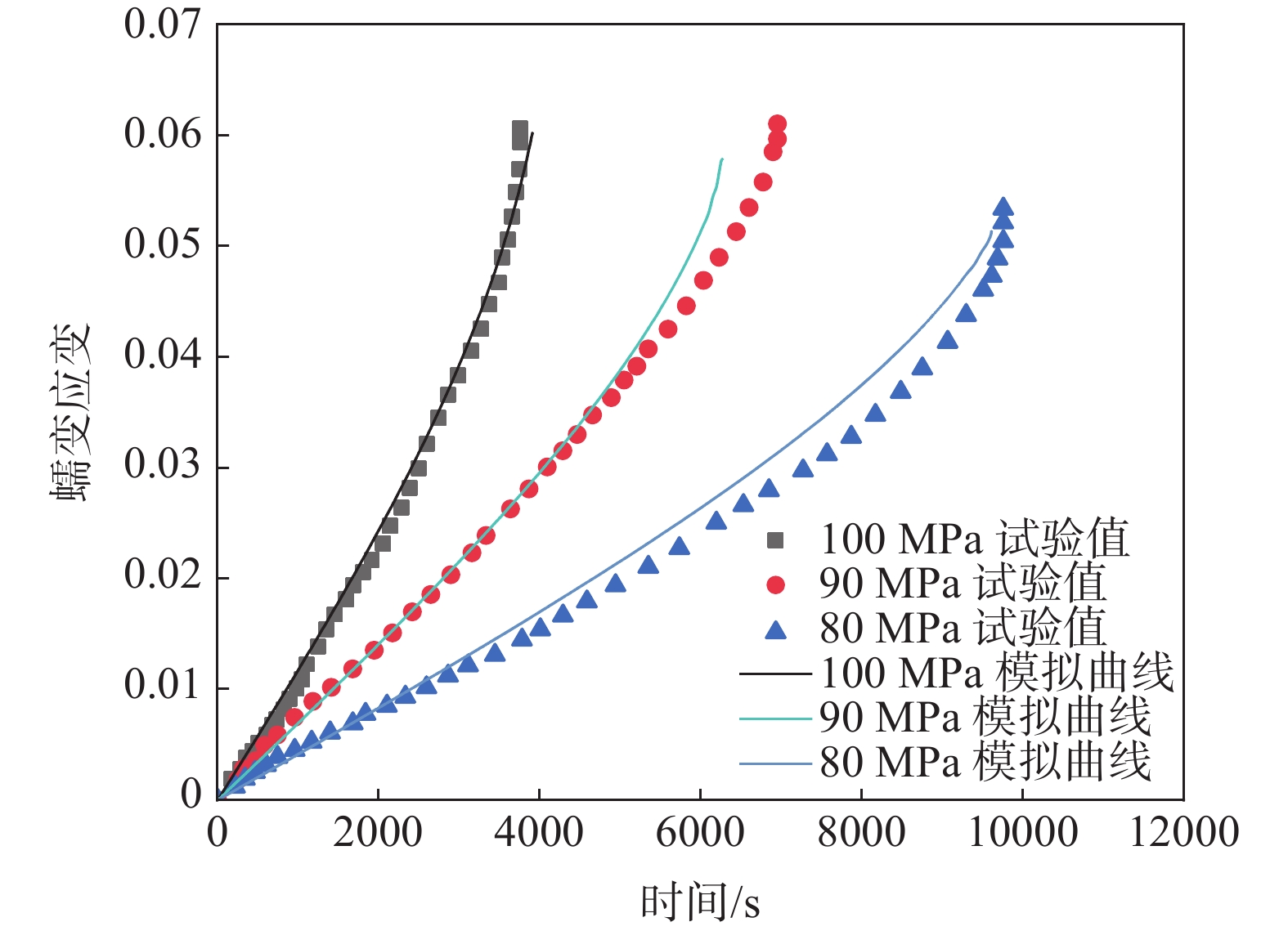
有限元得到的结果如图4所示。
由图4可得知,有限元模拟的蠕变曲线与使用试验结果绘制得到的蠕变曲线拟合效果不错。结果表明:有限元模拟能够较为完整地模拟出蠕变典型的三个阶段的完整过程,特别是100 MPa以下,模拟结果和试验曲线重合度较高,但是在80、90 MPa下蠕变的第三阶段仍然存在一定的偏差,其原因可能是在对数据进行拟合时,归一化处理得到的参数值并不准确,因此模拟时会与试验曲线存在一定的偏差。但同时也说明,基于Sinh模型的子程序较好地模拟了GH3128的蠕变行为,同时也表明了Sinh模型在蠕变的有限元模拟过程中具有较高的准确性和便利性。
5. 结论
1)由3种模型的模拟损伤过程可得,K-R模型损伤变量在蠕变后期存在奇异性,而Sinh模型和Liu-M模型能够克服这种限制,并且比K-R蠕变模型损伤演化过程要缓和。
2)在使用蠕变损伤模型对GH3128合金的蠕变寿命预测时,发现Sinh模型预测能力最好。
3)通过比较有限元模拟与试验蠕变曲线,证明基于Sinh模型的Creep子程序二次开发是可靠合理的,将Sinh蠕变模型嵌入ABAQUS中,可以高效、准确地对GH3128合金高温蠕变进行有限元分析。
-
表 1 三种损伤模型方程参数
Table 1. Equation parameters of the three damage models
模型 参数 K-R模型 $ A $:4.36 e-15;$ {n}_{1} $:4.71;$ {M}_{1} $:4.38 e-14;$ \varnothing $:15.01;$ {\chi }_{1} $:4.31 Liu-M模型 $ C $:4.36 e-15;$ {n}_{2} $:4.71;$ {M}_{3} $:6.02 e-13;$ p $:4.31;$ q $:4.32 Sinh模型 $ {\rm B} $:1.34 e-7;$ {\mathrm{\sigma }}_{\mathrm{s}} $:19.41;$ {\sigma }_{t} $:22.80;
$ {M}_{2} $:6.15 e-6;$ \phi $:4.50;λ:2.50;$ {\chi }_{2} $:1表 2 模型蠕变寿命预测及误差对比
Table 2. Comparison of creep life prediction and errors of the models
应力/
MPa试验
寿命/sK-R模型 Sinh模型 Liu-M模型 蠕变
寿命/s误差/% 蠕变
寿命/s误差/% 蠕变
寿命/s误差/% 100 3696.8 3914.5 5.9 4049.7 9.5 3984.7 7.8 90 6917.5 6164.4 10.8 6322.11 8.6 6275.0 9.3 80 9721.0 10241.5 5.2 9742.7 0.2 10425.2 7.2 -
[1] LIU T Y, LAI Y, FU J H, et al. High temperature rheological behavior and microstructure evolution of GH3128 alloy[J]. Metal Heat Treatment, 2020,45(6):141-148. (刘庭耀, 赖宇, 付建辉, 等. GH3128合金的高温流变行为与组织演变规律[J]. 金属热处理, 2020,45(6):141-148.LIU T Y, LAI Y, FU J H, et al. High temperature rheological behavior and microstructure evolution of GH3128 alloy[J]. Metal Heat Treatment, 2020, 45(6): 141-148. [2] YANG B, WU S H, BAO Z N, et al. Thermal deformation behavior and phenomenological constitutive model of GH3128 alloy[J]. Forging Technology, 2022,47(5):226-234. (杨波, 吴诗豪, 包振男, 等. GH3128合金热变形行为与唯象本构模型[J]. 锻压技术, 2022,47(5):226-234.YANG B, WU S H, BAO Z N, et al. Thermal deformation behavior and phenomenological constitutive model of GH3128 alloy[J]. Forging Technology, 2022, 47(5): 226-234. [3] YUAN Z F, JIANG J, CHENG Z W, et al. Study on high temperature mechanical properties of fiber laser GH3128 lap joint[J]. China Laser, 2022,49(21):170-178. (袁振飞, 蒋劲, 程智伟, 等. 光纤激光GH3128搭接接头高温力学性能研究[J]. 中国激光, 2022,49(21):170-178.YUAN Z F, JIANG J, CHENG Z W, et al. Study on high temperature mechanical properties of fiber laser GH3128 lap joint[J]. China Laser, 2022, 49(21): 170-178. [4] AN F P, LIU X W, ZHANG L J, et al. Dramatic improvement of the strength of laser welded joints of Nb521 to GH3128 by adding pure copper as an interlayer[J]. International Journal of Refractory Metals and Hard Materials, 2023,116:106367. doi: 10.1016/j.ijrmhm.2023.106367 [5] XU G, PENG L D, JIN H W. Creep damage characteristics and constitutive model of water-bearing coal[J]. Mining Research and Development, 2023,43(9):152-157. (徐刚, 彭来栋, 金洪伟. 含水煤体蠕变损伤特性及本构模型研究[J]. 矿业研究与开发, 2023,43(9):152-157.XU G, PENG L D, JIN H W. Creep damage characteristics and constitutive model of water-bearing coal[J]. Mining Research and Development, 2023, 43(9): 152-157. [6] PAN X K, ZHOU X P, ZOU Y Y, et al. Creep mechanical properties and creep damage model of sandstone considering temperature effect based on acoustic emission[J]. Fatigue Fracture of Engineering Materials Structures, 2023,47(1):35-55. [7] MAO X P, GUO Q, ZHANG S Y, et al. Experimental study on creep damage of nickel-based alloy C276[J]. Nuclear Power Engineering, 2013,34(2):86-89. (毛雪平, 郭琦, 张声远, 等. 镍基合金C276蠕变损伤的实验研究[J]. 核动力工程, 2013,34(2):86-89. doi: 10.3969/j.issn.0258-0926.2013.02.020MAO X P, GUO Q, ZHANG S Y, et al. Experimental study on creep damage of nickel-based alloy C276[J]. Nuclear Power Engineering, 2013, 34(2): 86-89. doi: 10.3969/j.issn.0258-0926.2013.02.020 [8] STEWART C M, GORDON A P. Strain and damage-based analytical methods to determine the Kachanov–Rabotnov tertiary creep-damage constants[J]. International Journal of Damage Mechanics, 2012,21(8):1186-1201. doi: 10.1177/1056789511430519 [9] HAQUE M S, STEWART C M. Finite element analysis of waspaloy using sinh creep-damage constitutive model under triaxial stress state[J]. Journal of Pressure Vessel Technology, 2016,138(3):031408. doi: 10.1115/1.4032704 [10] ZHANGN Q, LIU X B, ZHU L, et al. Comparison of creep damage models based on P91 steel[J]. Journal of Northwest University: Natural Science, 2017,47(5):711-716. (张琦, 刘新宝, 朱麟, 等. 基于P91钢的蠕变损伤模型比较[J]. 西北大学学报: 自然科学版, 2017,47(5):711-716.ZHANGN Q, LIU X B, ZHU L, et al. Comparison of creep damage models based on P91 steel[J]. Journal of Northwest University: Natural Science, 2017, 47(5): 711-716. [11] MURAKAMI S, LIU Y, MIZUO M. Computational methods for creep fracture analysis by damage mechanics[J]. Compute methods in applied mechanics and engineering, 2000,183(1-2):15-33. doi: 10.1016/S0045-7825(99)00209-1 [12] ZHAO L. Study on creep damage mechanism of P92 steel welded joints[D]. Tianjin: Tianjin University, 2009. (赵雷. P92钢焊接接头的蠕变损伤机理研究[D]. 天津:天津大学, 2009.ZHAO L. Study on creep damage mechanism of P92 steel welded joints[D]. Tianjin: Tianjin University, 2009. [13] XU D F. Study on creep characteristics of cooling tube of GH3128 superalloy intermediate heat exchanger[D]. Qinhuangdao: Yanshan University, 2019. (徐殿峰. GH3128高温合金中间换热器冷却管蠕变特性研究[D]. 秦皇岛:燕山大学, 2019.XU D F. Study on creep characteristics of cooling tube of GH3128 superalloy intermediate heat exchanger[D]. Qinhuangdao: Yanshan University, 2019. [14] KACHANOV L M. Rupture time under creep conditions[J]. International Journal of Fracture, 1999,97(1):11-18. [15] RABOTNOV Y N, LECKIE F A, PRAGERW W. Creep problems in structural members[J]. Journal of Applied Mechanics, 1970,37(1):249. [16] CHEN X, ZHOU G Y, TU S D. Finite element analysis of creep crack propagation of T-brazed joint[J]. Mechanical Strength, 2014,36(5):790-796. (陈兴, 周帼彦, 涂善东. T型钎焊接头蠕变裂纹扩展的有限元分析[J]. 机械强度, 2014,36(5):790-796.CHEN X, ZHOU G Y, TU S D. Finite element analysis of creep crack propagation of T-brazed joint[J]. Mechanical Strength, 2014, 36(5): 790-796. -






 下载:
下载:



 下载:
下载: