Study on the effect of multi area controllable electromagnetic braking on behavior of non-uniform molten steel flow and steel-slag interface in the mold
-
摘要: 连铸过程中，因水口堵塞引发的结晶器内部钢液流动畸变是影响铸件质量和生产效率的关键因素之一。为解决此问题，文中提出多区域独立可控电磁制动技术，以改善钢液流态，减少水口堵塞带来的负面影响。首先，选定板坯结晶器作为研究对象，构建电磁连铸结晶器内钢液流动与渣金界面行为分析模型；其次，对比分析无电磁制动、现行全幅一段电磁制动以及多区域独立可控电磁制动作用下，结晶器内部钢液非均匀流动特性与渣金界面的演变规律。模拟结果表明，在单侧水口发生25%堵塞的情况下，相较于全幅一段电磁制动，多区域独立可控电磁制动所产生的制动效应对非堵塞侧结晶器内钢液的流动控制效果更显著。与未施加电磁制动时相比，当施加的磁场强度为0.3 T时，全幅一段电磁制动结晶器内非堵塞侧钢液表面最大流速和界面最大波高分别增加了16.7%和1.6%，而多区域独立可控电磁制动结晶器内非堵塞侧钢液表面最大流速和界面最大波高分别降低了16.7%和48.4%。可见，采用多区域独立可控电磁制动可实现分区域控制结晶器内部钢液流动，从而改善流场的对称性，并减少因水口堵塞引起的流动不对称现象。Abstract: In the process of continuous casting, the distortion of molten steel flow in mold caused by nozzle clogging is a key factor affecting the quality and production efficiency of castings. To solve this problem, a multi area controllable electromagnetic braking (MAC-EMBr) technology is proposed to improve flow state of molten steel and reduce negative impact of nozzle clogging. Firstly, a slab mold is selected as the research object to establish an analytical model of molten steel flow and steel-slag interface behavior in electromagnetic continuous casting mold. Secondly, the fluid-flow-related phenomena of three casting cases in the slab mold, i.e., No-EMBr, Ruler-EMBr, and MAC-EMBr, are further investigated numerically to evaluate the metallurgical capability of the MAC-EMBr, including the non-uniform flow characteristics of molten steel and the evolution pattern of steel-slag interface inside the mold. According to the simulation results, with a 25% blockage rate of a single-side nozzle, the braking effect of the Ruler-EMBr on the backflow in the upper region of the mold is not remarkably. In detail, when the magnetic flux density reaches 0.3 T, the maximum magnitude of the surface velocity and the maximum amplitude of the level fluctuation on non-clogging side with the Ruler-EMBr are 16.7% and 1.6% higher than those with No-EMBr, respectively. This is not conducive to the stability of steel-slag interface in the mold. However, under the same magnetic flux density as the Ruler-EMBr, the application of MAC-EMBr has great potential to suppress the upward backflow on the non-clogging side. In comparison with No-EMBr, the maximum magnitude of the surface velocity and the maximum amplitude of the level fluctuation with the MAC-EMBr are decreased by 16.7% and 48.4%, respectively. As a result, the flow of molten steel in the mold can be well controlled in different regions with the MAC-EMBr, so as to improve the symmetry of the flow field and reduce the flow asymmetry caused by nozzle clogging.
-
0. 引言
连铸过程中，结晶器内钢液非均匀流动而引发的偏流现象对铸件物理特性和生产效能会造成显著负面影响，优化并控制结晶器内的钢液流动模式，以防止偏流发生，对于提高铸坯质量和生产效率至关重要[1]。研究表明，水口堵塞是导致结晶器内钢液流动异常，产生偏流现象的一个关键因素。当水口发生部分或完全堵塞时，结晶器内钢液的自然流动受到阻碍，导致钢液水口出流流量减少，原有钢液均匀流动模式被破坏，表现为局部区域流速增加，其他区域则可能出现流动停滞或逆流现象[2−3]。具体而言，在高速流动区域，局部流速的增加使该区域的渣金界面受到冲击后，界面扰动加剧。而随着界面扰动的增强，钢液与渣层间附着的稳定性减弱，使得钢液裸露区域扩大，氧化风险提高。在低流速或逆流区域，渣金界面则可能因钢液的低流动性而无法得到充分更新，进而导致该区域的渣膜厚度增加，粘度增大，形成所谓的“死区”。而这些“死区”的存在不仅阻碍有效热传递，还增加局部过冷的可能性，最终影响热传递效率和结晶器壁的散热。
可见，水口堵塞不仅改变结晶器内部钢液的流动特性，促使流态发生畸变，还间接影响结晶器内部热交换过程，增加铸件内部产生裂纹、气孔等缺陷的风险。因此，为避免水口堵塞带来的负面影响，冶金工程师通常采用多种措施，如优化结晶器设计、改进浇注条件、应用电磁搅拌和制动技术等[4−7]。其中，电磁制动技术作为一种有效控制流体流动的技术，可通过电磁力改变钢液中的电流分布，以此来抑制或引导钢液的流动，从而减少因水口堵塞引起的钢液流动畸变[8]。现已应用的典型电磁制动技术包括区域型电磁制动技术(Local-EMBr)、全幅一段电磁制动技术(Ruler-EMBr)以及全幅二段电磁制动技术(FC-Mold)，这些技术在流体控制方面具有显著成效，但存在结晶器高度方向磁场作用区域不足的问题[9−13]。这意味着在非直接磁场作用区，尤其是结晶器上回流区、水口射流冲击区以及弯月面区，钢液的流动特性难以得到有效调控，易导致流体动力学的不稳定性，特别是在高速浇注条件下，这种磁场作用区域的局限性尤为显著[14]。
为解决此类问题，课题组相继提出立式及立式组合电磁制动技术[15−18]。其中，立式电磁制动技术通过在结晶器窄面附近布置的两对立式磁极，可实现对结晶器上回流区、水口射流冲击区以及弯月面区内钢液流动的独立控制，但其对下回流区钢液流动的控制存在不足。为弥补这一不足，立式组合电磁制动技术在立式电磁制动技术的基础上，增加一对水平磁极以有效控制下回流区钢液的流动。但立式组合电磁制动技术的电源控制系统存在局限性，仅通过缠绕于水平磁极的励磁线圈供电，导致与水平磁极相连的两对立式磁极无法获得独立电力供应。这在面对如连铸过程中因水口堵塞引发的钢液流动异常时，限制了立式组合电磁制动技术对结晶器内各区域钢液流动的独立调控能力。为突破这一局限性，作者提出多区域独立可控电磁制动技术，旨在保留立式组合电磁制动技术优势的同时，确保对结晶器内各关键区域钢液流动的全面、灵活且高效的独立调控，以应对各种复杂工况下的钢液流动控制需求。
为此，课题组基于稳恒磁场理论和电磁流体力学理论，以常规板坯结晶器作为研究对象，构建电磁连铸过程钢液非均匀流动与渣金界面行为分析模型，深入模拟研究浸入式水口单侧出口堵塞时，多区域独立可控电磁制动对结晶器内三维电磁场、钢液流动及渣金界面分布的影响。同时，对比评价无电磁制动、现行全幅一段电磁制动以及多区域独立可控电磁制动作用下，板坯结晶器内钢液非均匀流动与渣金界面行为的演变规律，为新型电磁制动技术的应用与优化提供理论依据和数据支持。
1. 数学模型
1.1 基本假设
为便于建立电磁连铸过程结晶器内三维多场耦合数学模型，对此作如下假设：结晶器内钢液流动为非稳态流动，且为均相和不可压缩牛顿流体；结晶器内保护渣为液态，忽略其他状态渣层的影响；忽略结晶器内传热、凝固及相关热行为；忽略结晶器振动和负锥度对钢液流动的影响；结晶器铜板、铁芯及钢液为各向同性介质，其电导率等物性参数设为常数[15]。
1.2 渣金界面两相流动控制方程
采用VOF方法模拟板坯结晶器内渣金界面两相流动和动态界面演变行为[15]。在VOF方法中，通过建立两相湍流瞬态流动模型，可确定移动界面界定网格流体体积，进而求解两相流中的钢液体积分数。其中，钢液体积分数可通过方程（1）获得。
$$ \frac{{\partial \varPhi }}{{\partial t}} + \nabla \varPhi {v_i} = 0 $$ (1) 式中，Ф表示钢液体积分数；Ф=1时表示主相钢液；Ф=0时表示次相保护渣；0<Ф<1表示相界面；vi表示钢液流动速度，m/s。
考虑到结晶器内主相钢液与次相保护渣分子间的相互作用力，界面张力在渣金界面上不可避免。为此，在动量方程中引入体积力作为源项，以考虑界面张力效应，其表达式如下：
$$ {F_{{\mathrm{Vol}},i}} = \sigma \frac{{\rho \kappa \nabla \varPhi }}{{0.5\left( {{\rho _{{\mathrm{st}}}} + {\rho _{{\mathrm{sl}}}}} \right)}} $$ (2) $$ \rho = {\rho _{{\mathrm{st}}}}\varPhi + {\rho _{{\mathrm{sl}}}}\left( {1 - \varPhi } \right) $$ (3) $$ \kappa = \nabla \cdot \left( {\frac{{\nabla \varPhi }}{{\left| \varPhi \right|}}} \right) $$ (4) 式中，FVol,i表示体积力源项，N/m3；ρ表示流体平均密度，kg/m3；ρst表示钢液密度，kg/m3；ρsl表示液渣密度，kg/m3；σ表示钢液电导率，S/m；κ表示表面平均曲率。
1.3 湍流流动控制方程
相较于其他双方程湍流模型，SST k-ω湍流模型在处理稳定与不稳定湍流问题上具有较高的计算精度。具体而言，在不同压力梯度条件下，该模型不仅能够精确模拟各种来流分离现象，还能够对湍流黏度的低雷诺数进行修正，从而增强在处理近壁面流动细节方面的准确性[15]。基于此，笔者采用SST k-ω湍流模型计算结晶器内部流场，涉及的方程如下：
连续性方程：
$$ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {v_i}} \right)}}{{\partial {x_{\text{i}}}}} = 0 $$ (5) 动量方程：
$$ \begin{split} &\frac{\partial\left(\rho v_i\right)}{\partial t}+\frac{\partial\left(\rho v_i v_j\right)}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_j}\left[\mu _ { {\mathrm{c f f }}} \left(\frac{\partial v_i}{\partial x_j}+\right.\right. \\ &\qquad \left.\left.\frac{\partial v_j}{\partial x_i}\right)+\right]\rho g_i+F_{{\mathrm{M}}, i}+F_{ {{\mathrm{Vol}},i }} \end{split} $$ (6) 湍动能方程：
$$ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + {v_j}\frac{{\partial \left( {\rho k} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\mathrm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - {Y_k} $$ (7) 湍动能比耗散率方程：
$$ \begin{split} &\frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + {v_j}\frac{{\partial \left( {\rho \omega } \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\mathrm{t}}}}}{{{\sigma _\omega }}}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right] +\\ &\qquad {G_\omega } - {Y_\omega } + {D_\omega } \end{split} $$ (8) 式(7)和（8）中，
$$ {\sigma _k} = \frac{1}{{{{{F_1}} \mathord{\left/ {\vphantom {{{F_1}} {{\sigma _{k,1}} + {{\left( {1 - {F_1}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {F_1}} \right)} {{\sigma _{k,2}}}}} \right. } {{\sigma _{k,2}}}}}}} \right. } {{\sigma _{k,1}} + {{\left( {1 - {F_1}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {F_1}} \right)} {{\sigma _{k,2}}}}} \right. } {{\sigma _{k,2}}}}}}}} $$ (9) $$ {\sigma _\omega } = \frac{1}{{{{{F_1}} \mathord{\left/ {\vphantom {{{F_1}} {{\sigma _{\omega ,1}} + {{\left( {1 - {F_1}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {F_1}} \right)} {{\sigma _{\omega ,2}}}}} \right. } {{\sigma _{\omega ,2}}}}}}} \right. } {{\sigma _{\omega ,1}} + {{\left( {1 - {F_1}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {F_1}} \right)} {{\sigma _{\omega ,2}}}}} \right. } {{\sigma _{\omega ,2}}}}}}}} $$ (10) $$ {G_k} = {\mu _t}\left\{ {2\left[ {{{\left( {\frac{{\partial {v_i}}}{{\partial {x_i}}}} \right)}^2} + {{\left( {\frac{{\partial {v_j}}}{{\partial {x_j}}}} \right)}^2}} \right] + {{\left( {\frac{{\partial {v_i}}}{{\partial {x_j}}} + \frac{{\partial {v_j}}}{{\partial {x_i}}}} \right)}^2}} \right\} $$ (11) 式（6）~（11）中，p表示压强，Pa；FM,i表示时均电磁力，N/m3；μeff表示有效黏度，kg/(m·s)；μ表示流体平均动力黏度，kg/(m·s)；μt表示湍流动力黏度，由剪切压力传输SST(Shear–Stress Transport)k–ω双方程湍流模型确定，kg/(m·s)；k表示湍动能，m2/s2；ω表示比耗散率，1/s；σk、σω表示湍流普朗特数；F1表示混合函数；Gω表示比耗散率产生项；Yk表示湍流动能耗散项；Yω表示比耗散率耗散项；Dω表示交叉扩散项；Gk表示湍流动能产生项。
1.4 电磁场控制方程
数值模拟结晶器内部流场与电磁场之间的相互作用时，通过Maxwell方程、介质本构方程及欧姆定律方程求解电磁感应方程，并利用电磁感应方法求解感应电流密度，具体方程如下：
电磁感应方程：
$$ \begin{split} &\frac{{\partial {b_i}}}{{\partial t}} + \left( {{v_i} \cdot \nabla } \right){b_i} = \frac{1}{{\mu \sigma }}{\nabla ^2}{b_i} + \left[ {\left( {{B_{0,i}} + {b_i}} \right) \cdot \nabla } \right]\\ &\qquad {v_i} - \left( {{v_i} \cdot \nabla } \right){B_{0,i}} \end{split} $$ (12) 电流密度方程：
$$ {J_i} = \frac{1}{\mu }\nabla \times {B_i} = \frac{1}{\mu }\nabla \times \left( {{B_{0,i}} + {b_i}} \right) $$ (13) 电磁力方程：
$$ {F_{{\mathrm{m}},i}} = {J_i} \times {B_i} = {J_i} \times \left( {{B_{0,i}} + {b_i}} \right) $$ (14) 式（12）~（14）中，vi为导电介质速度矢量，m/s；bi为导电钢液穿过磁场时产生的磁场强度，T；B0,i为外部磁场强度，T；Bi为磁场强度，T；μ为介质磁导率，H/m；Ji为电流密度，A/m2；Fm,i为洛伦兹力，N/m3。
1.5 边界条件
浸入式水口顶端为结晶器入口，定义速度入口边界条件；计算域底部为结晶器出口，定义质量出口边界条件；结晶器内上液面为自由液面，定义对称边界条件；水口壁面和结晶器壁面定义无滑移绝缘壁面边界条件，其近壁面区域的湍流特性依据SST k–ω双方程湍流模型的壁面函数确定，此外沿壁面法线方向的感应电流密度分量为零。计算过程所涉及的主要参数见表1。
表 1 板坯结晶器计算参数Table 1. Computational parameters of slab mold铸坯断面/（mm×mm） 结晶器长度/mm 结晶器计算域/mm 水口双侧孔尺寸/mm 水口浸入深度/mm 水口内径/mm 拉坯速度/(m∙min−1) 1450 ×230800 4000 65×80 170 80 1.8 钢液密度/(kg∙m−3) 钢液黏度/(Pa∙s) 钢液电导率/(S∙m−1) 钢液磁导率/(H∙m−1) 液渣密度/(kg∙m−3) 表面张力/(N∙m−1) 磁场强度/T 7020 0.0062 7.14×105 1.26×106 3500 1.2 0.1 0.2 0.3 2. 几何模型
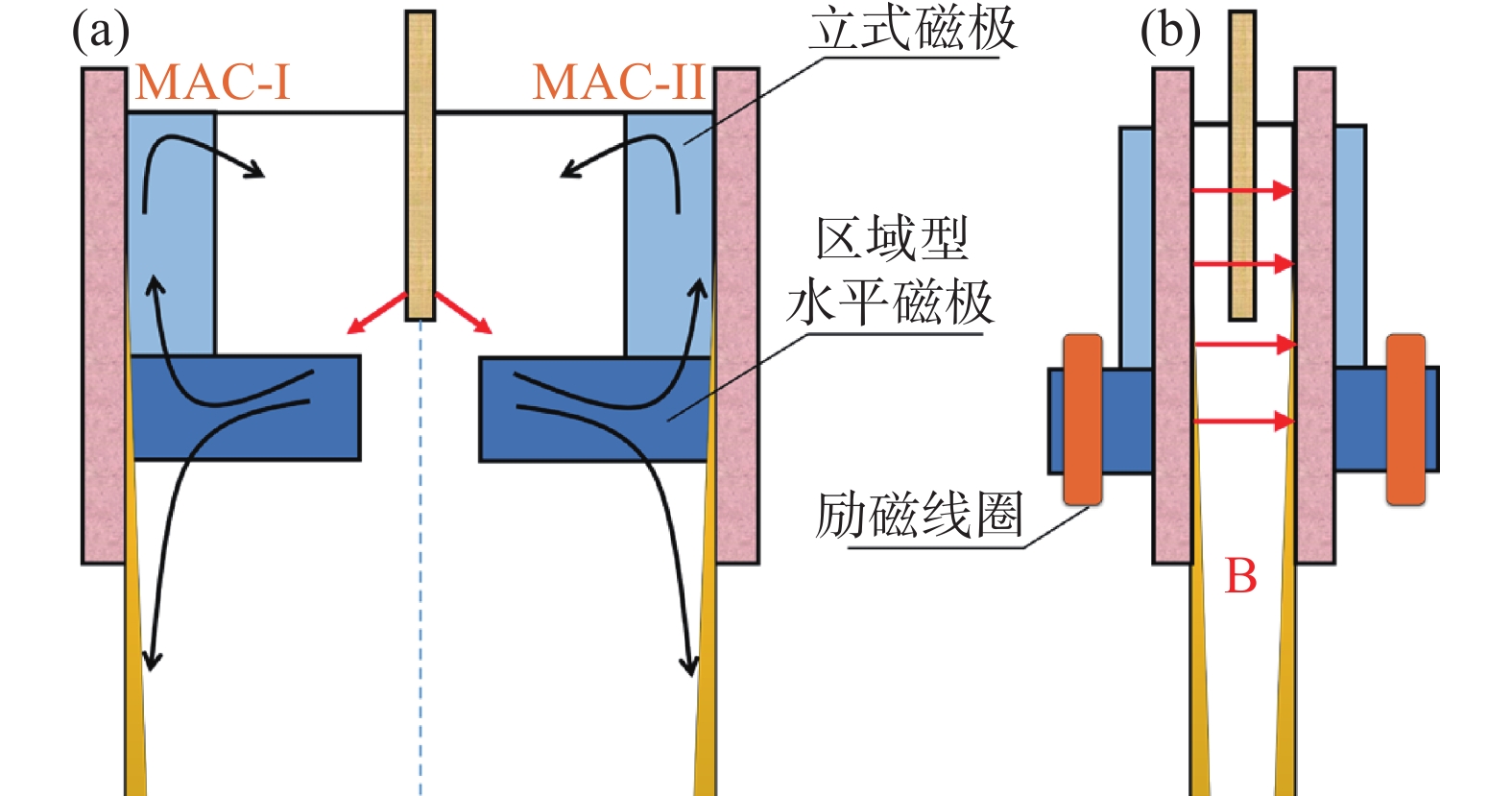
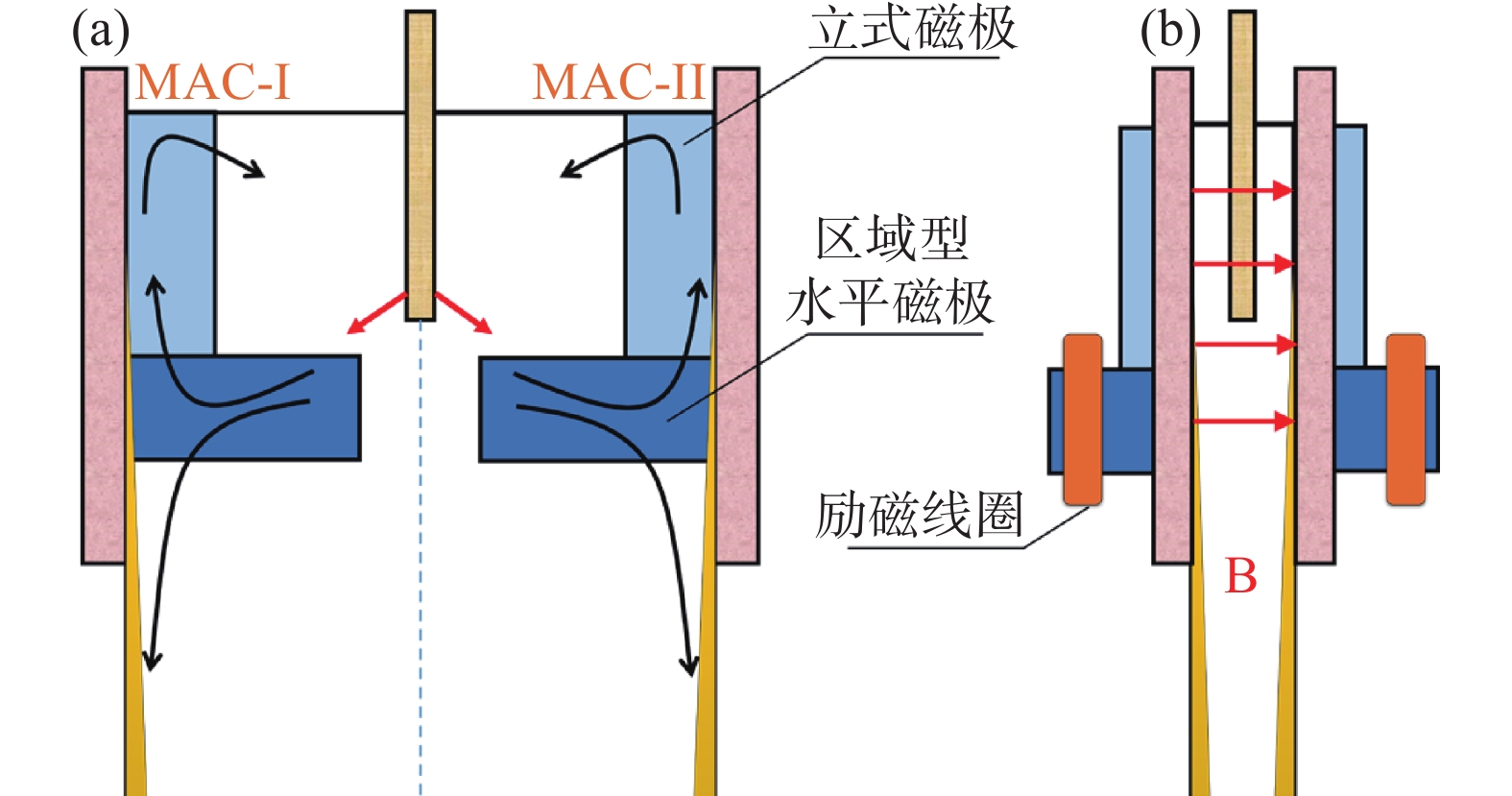
多区域独立可控电磁制动装置如图1所示。多区域独立可控电磁制动装置由MAC-I和MAC-II两组磁极组成，每组磁极包括一对立式磁极和一对区域型水平磁极，使磁极布置方式呈“L”型分布。其中，MAC-I和MAC-II磁极可根据板坯结晶器内钢液流动情况，独立地调节其位置和线圈的电流强度，从而实现对不同区域钢液流动的独立控制。具体而言，靠近结晶器两侧窄面布置的立式磁极，分别通过独立电源控制系统和缠绕于区域型电磁制动装置的励磁线圈，可产生覆盖于结晶器上回流区、水口射流冲击区以及弯月面区的直流磁场，进而弥补区域型以及全幅一段型电磁制动技术对结晶器上回流区制动不足的弊端。同时，位于浸入式水口下方的区域型水平磁极，可产生覆盖于结晶器下回流区的直流磁场，保留区域型以及全幅一段型电磁制动技术对结晶器下回流区钢液流动的控制优势。可见，多区域独立可控电磁制动装置采用的“L”型磁极布置方式，在保持了区域型电磁制动装置对于特定区域内钢液流动有效控制优势的同时，通过新增加的立式磁极，显著增强了对结晶器内钢液流动的多维度和多区域的独立控制能力。
3. 数学模型及网格无关性验证
3.1 数学模型验证
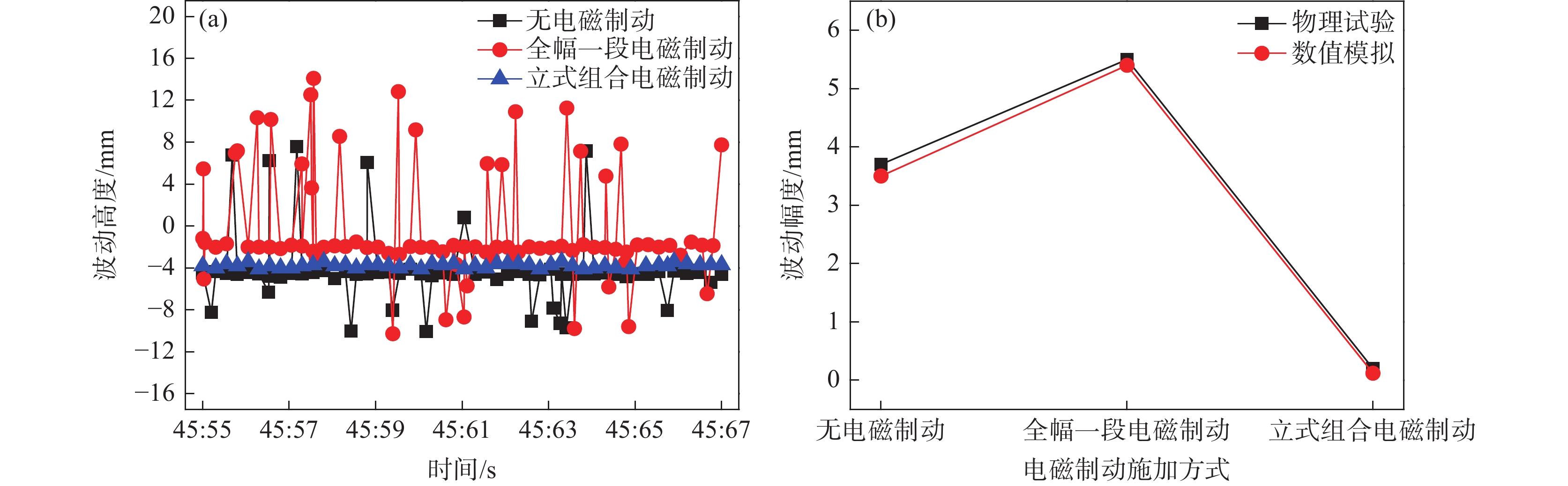
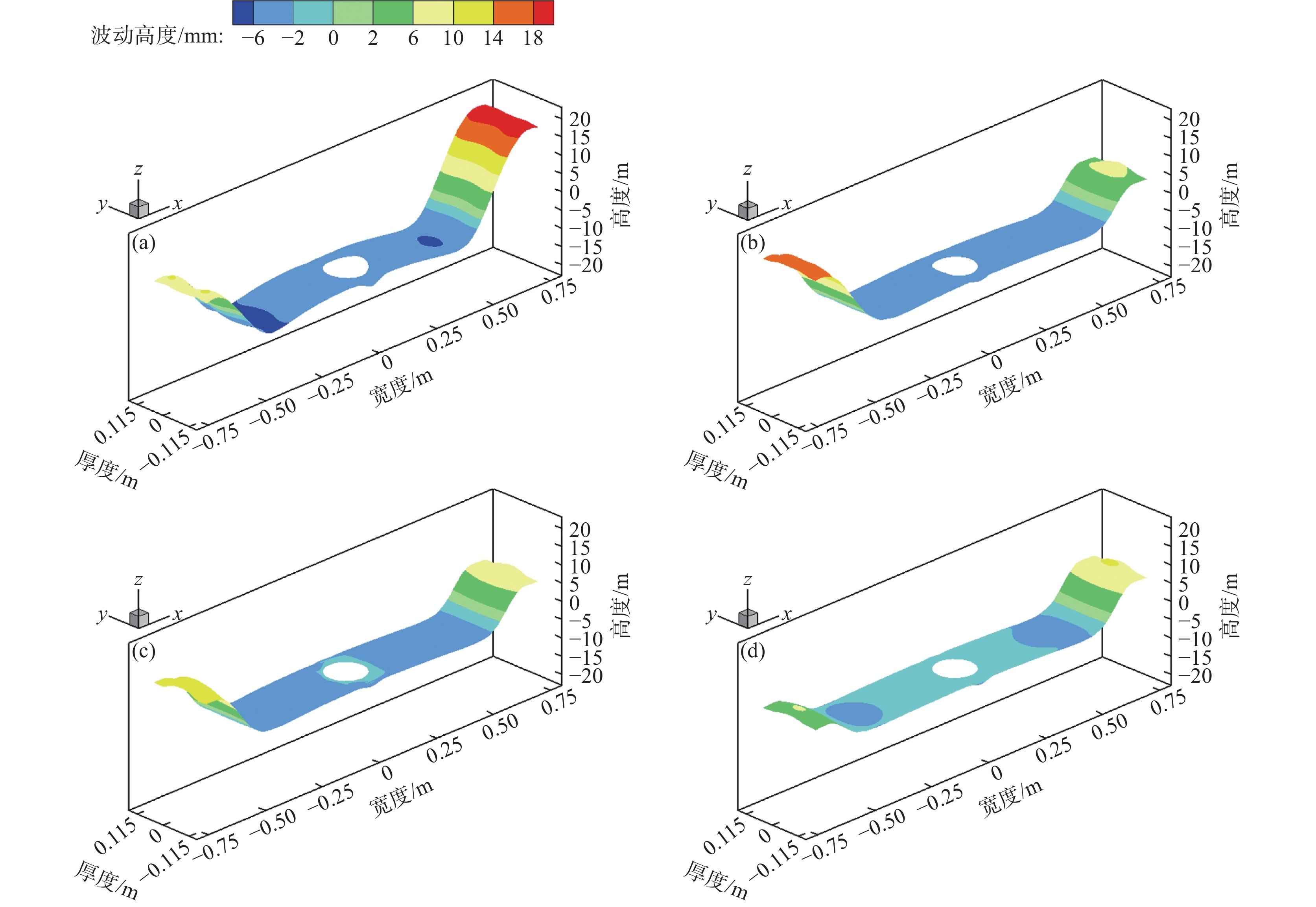
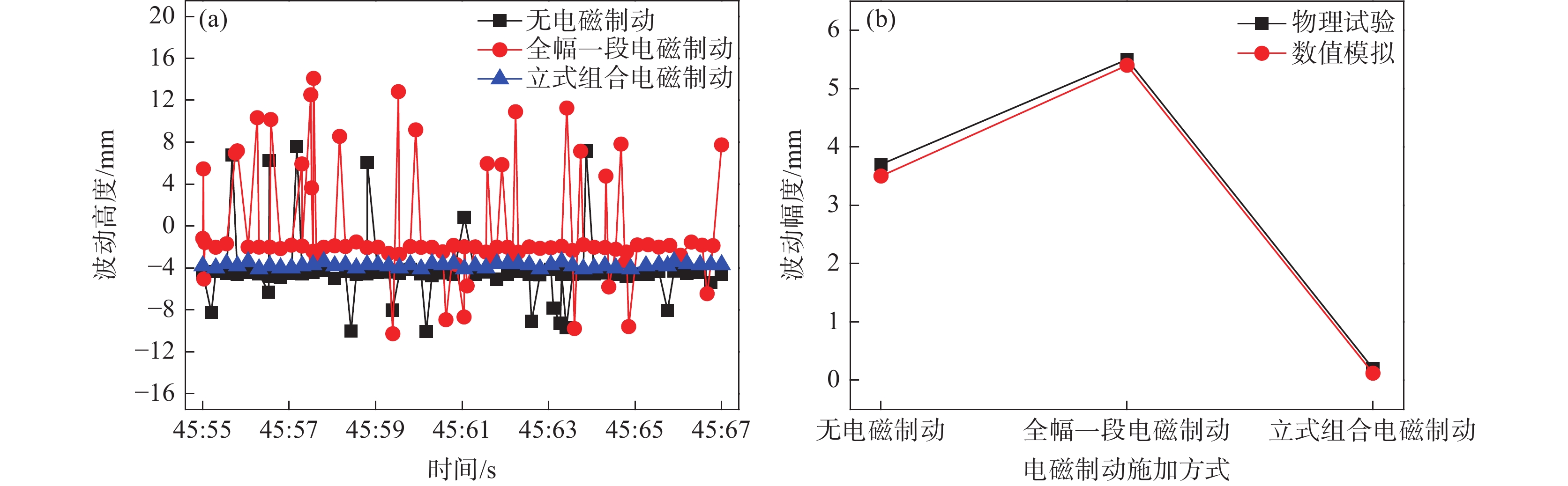
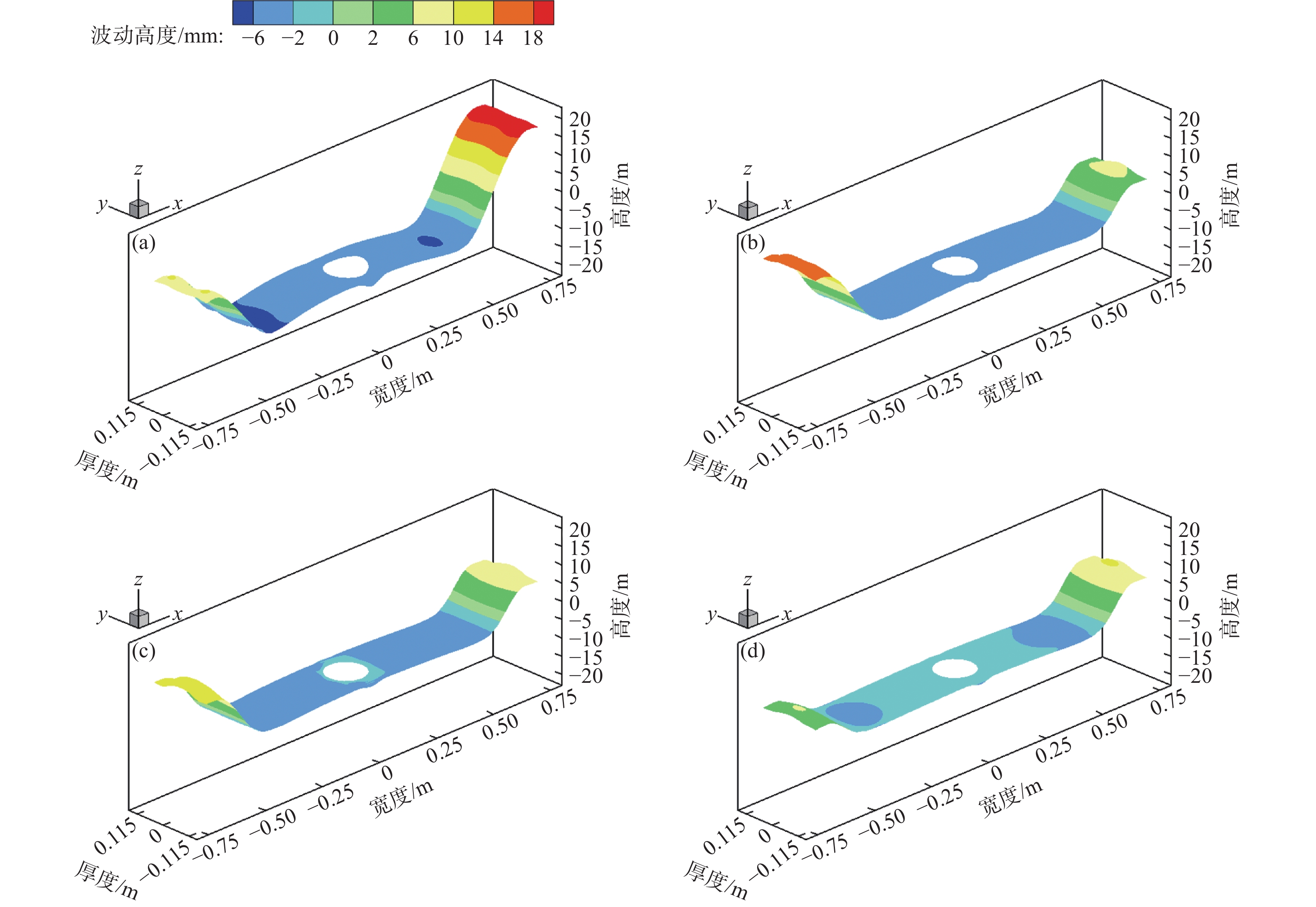
课题组前期已对板坯连铸结晶器内钢液流动与渣金界面行为开展了大量的研究工作，并通过铅锡铋合金连铸实验平台构建了相应的数值仿真模型，用以验证结晶器电磁连铸过程三维多物理场耦合数学模型的准确性[17]。图2为试验和数值模拟板坯结晶器内表面波动结果，结果表明，在有、无磁场作用时，金属液表面波动特性的模拟结果与实测结果高度吻合。
图 2 试验测量和数值模拟结晶器内液面波动结果(a) 试验测量结果；(b) 试验和模拟比对结果Figure 2. Experimental measurement and numerical simulation of level fluctuation heights in the mold3.2 网格无关性验证
网格无关性验证方法是判断数值模拟结果可信度的重要标准之一，该方法通过改变网格的数量和疏密程度，判断在一定范围内的网格变化对数值模拟结果的影响，以此检验在该范围内的网格数量是否满足无关性[18]。基于此，为确保计算结果的准确性与所采用的网格数量无关，文中对物理模型的网格数量进行网格无关性验证。网格无关性验证结果如表2所示。其中，无关性验证过程所需的基本参数为铸坯断面
1450 mm × 230 mm，拉坯速度1.8 m/min，磁场强度0 T。结果表明，网格节点数从M1至M3逐渐增加的过程中，渣金界面波动高度最大值的相对误差远小于5%。据此，确认M1至M3区间内的网格数量满足无关性要求，但考虑到实际工程中计算效率与精确度的平衡，在不影响计算精度的前提下，择取最低密度网格M1作为运算基准。表 2 计算域内不同网格节点数的误差统计结果Table 2. Statistic results of error with different grid node numbers in the computational domain网格 M1 M2 M3 网格节点数 490,000 735,000 1,102,500 $ {h_{{{\text{M}}_i}}} $ 25.8 25.2 24.9 $ {\delta _h} = {{\left| {{h_{{{\text{M}}_i}}} - {h_{{{\text{M}}_1}}}} \right|} \mathord{\left/ {\vphantom {{\left| {{h_{{{\text{M}}_i}}} - {h_{{{\text{M}}_1}}}} \right|} {{h_{{{\text{M}}_1}}}}}} \right. } {{h_{{{\text{M}}_1}}}}} $ 0 2.3% 3.5% 注：表中h为渣金界面波动高度最大值，即波峰与波谷间的垂直距离，mm；δh为渣金界面波动高度的相对误差，%。 4. 结果与讨论
4.1 多区域独立可控电磁制动结晶器内磁场强度分布特征
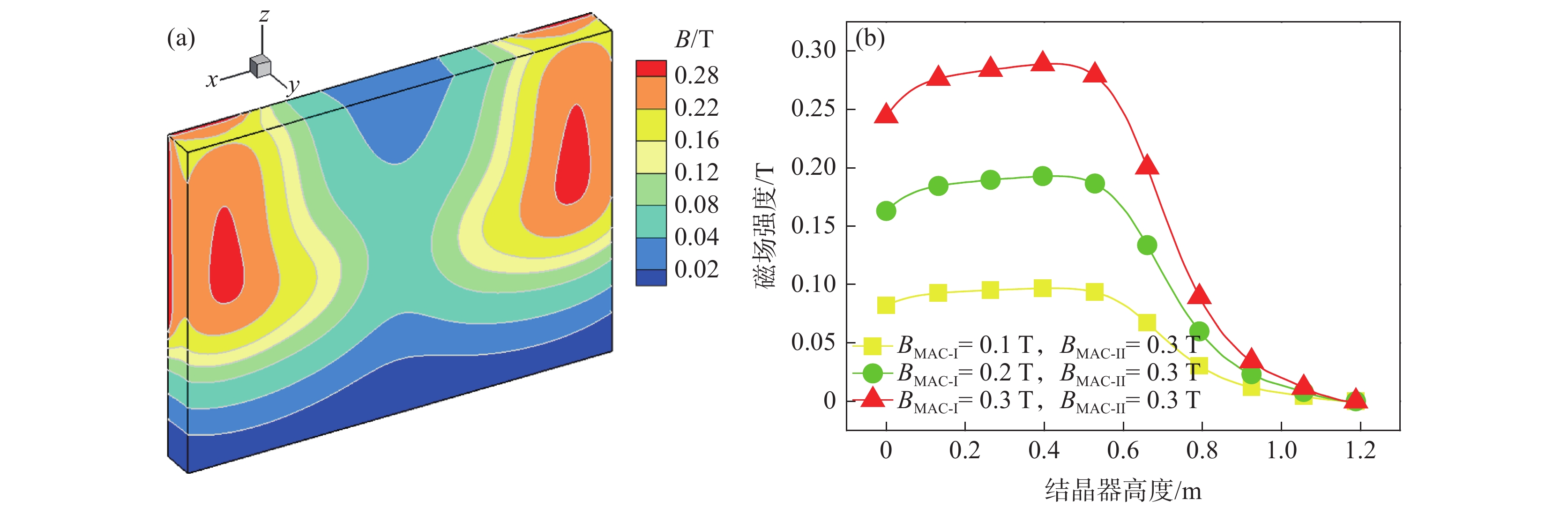
多区域独立可控电磁制动结晶器内磁场强度分布如图3所示。由图3(a)可见，在立式磁极和水平区域磁极的作用下，多区域独立可控电磁制动产生的稳恒磁场均匀覆盖于结晶器上回流区、水口射流冲击区以及弯月面区，且磁场强度大小由磁极中心向磁极两侧呈梯度递减。由图3(b)可见，在结晶器宽面中心位置处，当MAC-I磁极作用于上回流区、射流冲击区以及弯月面区的最大磁场强度由0.1 T逐渐增加至0.3 T时，位于立式磁极宽度中心线上(x = ‒0.6 m，y = 0～1.2 m，z = 0 m)的磁场强度在射流冲击区内达到最大值0.29 T(x = ‒0.43 m，z = 0 m)。
图 3 多区域独立可控电磁制动结晶器内磁场强度分布(a) 结晶器内磁场强度；(b) 沿结晶器高度方向宽面中心截面磁场强度Figure 3. Distribution of magnetic field intensity in the mold with MAC-EMBr4.2 多区域独立可控电磁制动结晶器内钢液流动特征
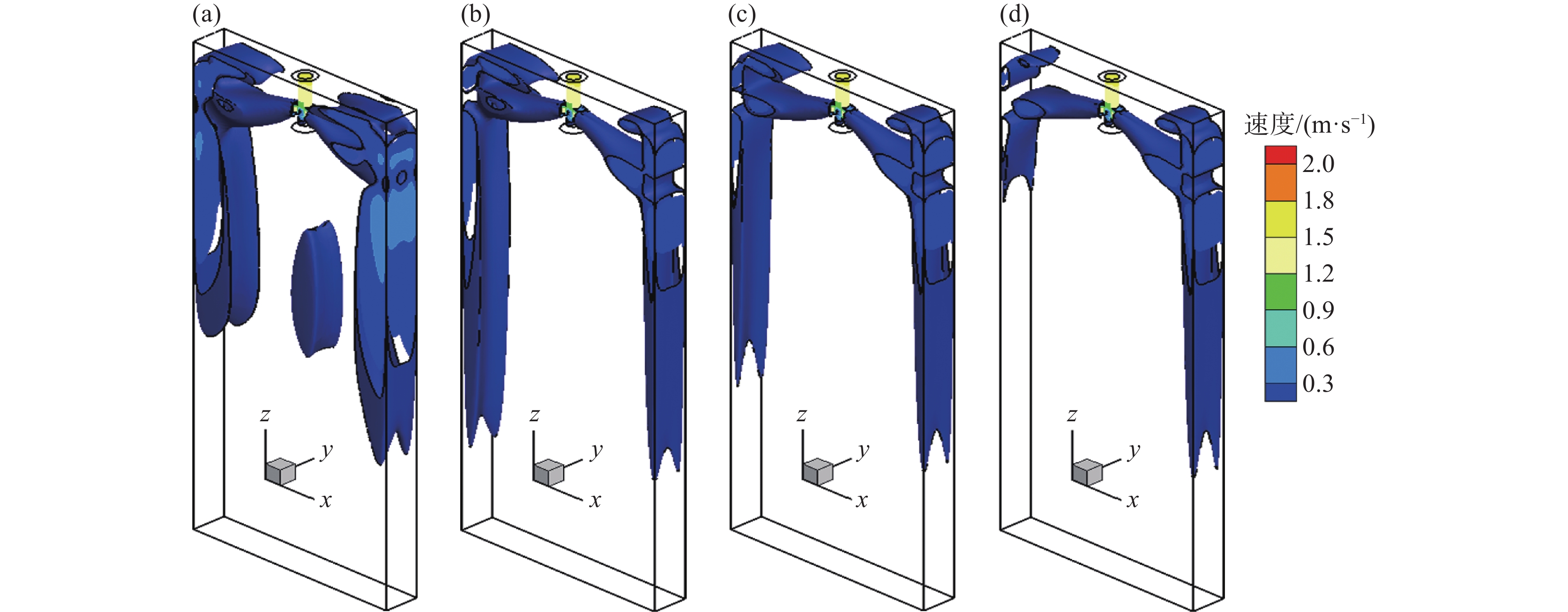
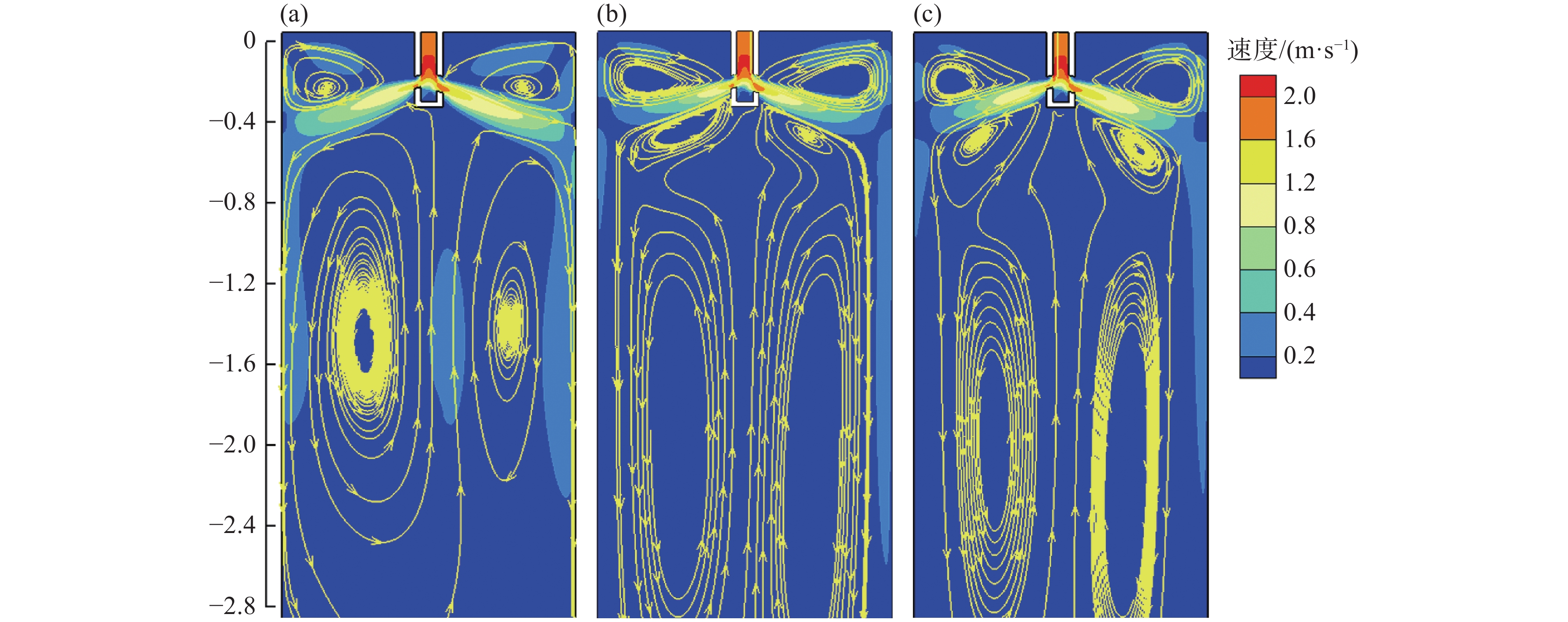
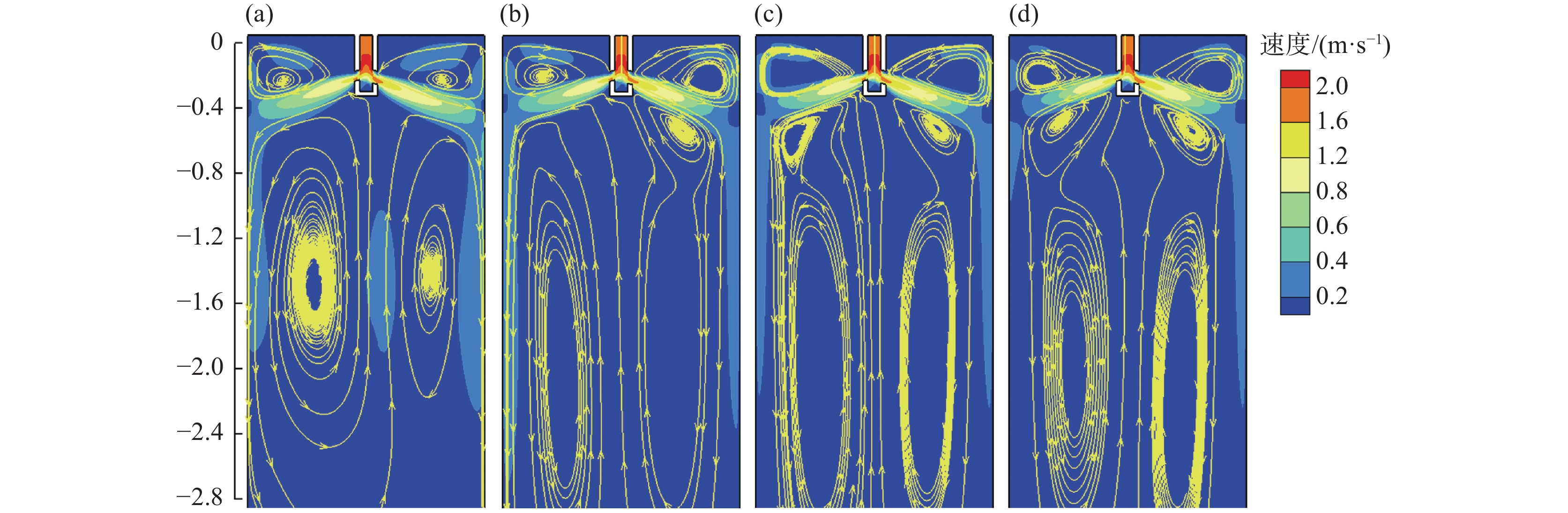
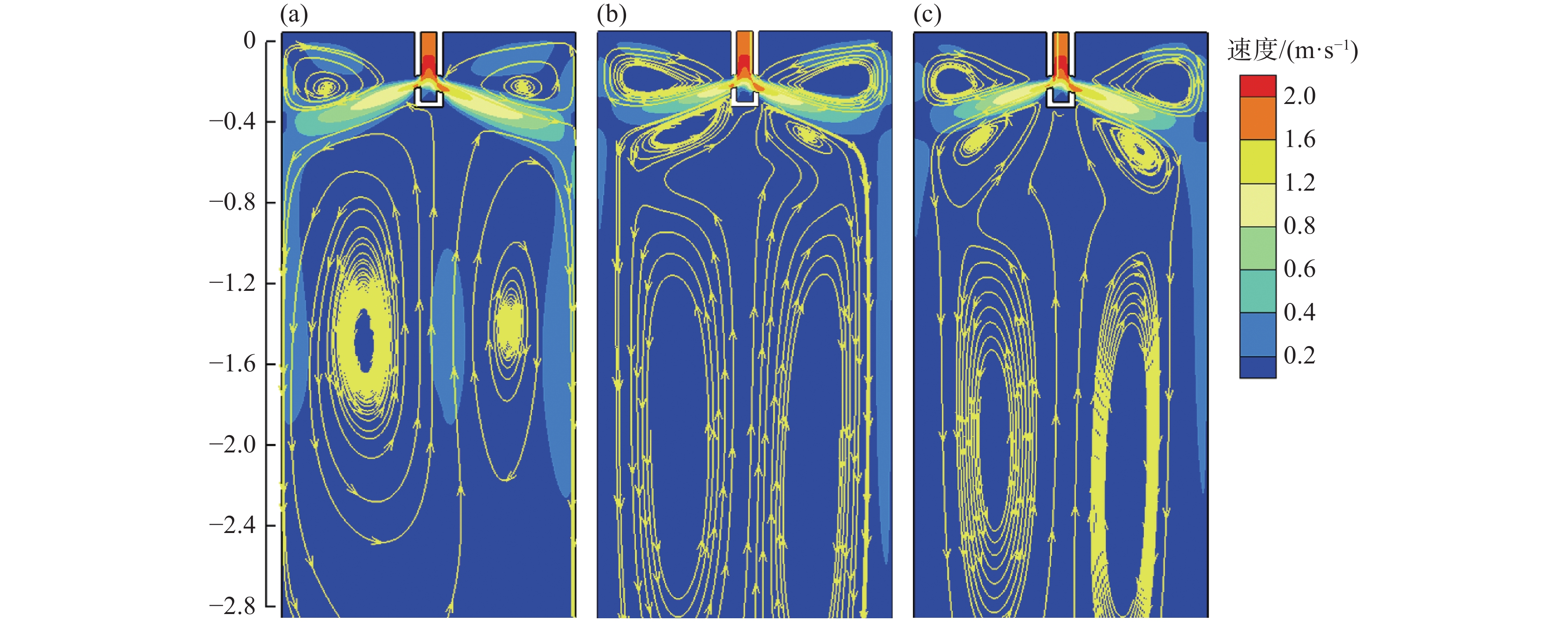
图4为有、无多区域独立可控电磁制动条件下，当浸入式水口的左侧出口堵塞25%时，结晶器宽面中心截面钢液速度云图和流线图。由图4可见，未施加电磁制动时，结晶器内部原本稳定且对称的钢液流动模式随即被破坏。在水口堵塞侧的出口处，钢液的流动受到阻碍，导致钢液流量减少，对应上回流区的钢液流动强度随之减弱。为了弥补堵塞侧钢液流量的损失，并维持结晶器内钢液总量的平衡，非堵塞侧的钢液流量增加。然而，这种流量的增加伴随上回流区的钢液流动强度和热交换过程加剧，导致渣金界面波动的不稳定性和结晶器内部钢液温度分布的不均匀性增加。
图 4 多区域独立可控电磁制动结晶器宽面中心截面钢液速度分布Figure 4. Velocity distribution in the central section of wide surface in the mold with MAC-EMBr(a) BMAC-I=BMAC-II=0 T；(b) BMAC-I=0.1 T，BMAC-II=0.3 T；(c) BMAC-I=0.2 T，BMAC-II=0.3 T；(d) BMAC-I=BMAC-II=0.3 T施加多区域独立可控电磁制动后，对于水口非堵塞侧的钢液流动，当保持MAC-II中水平磁极的电流强度为
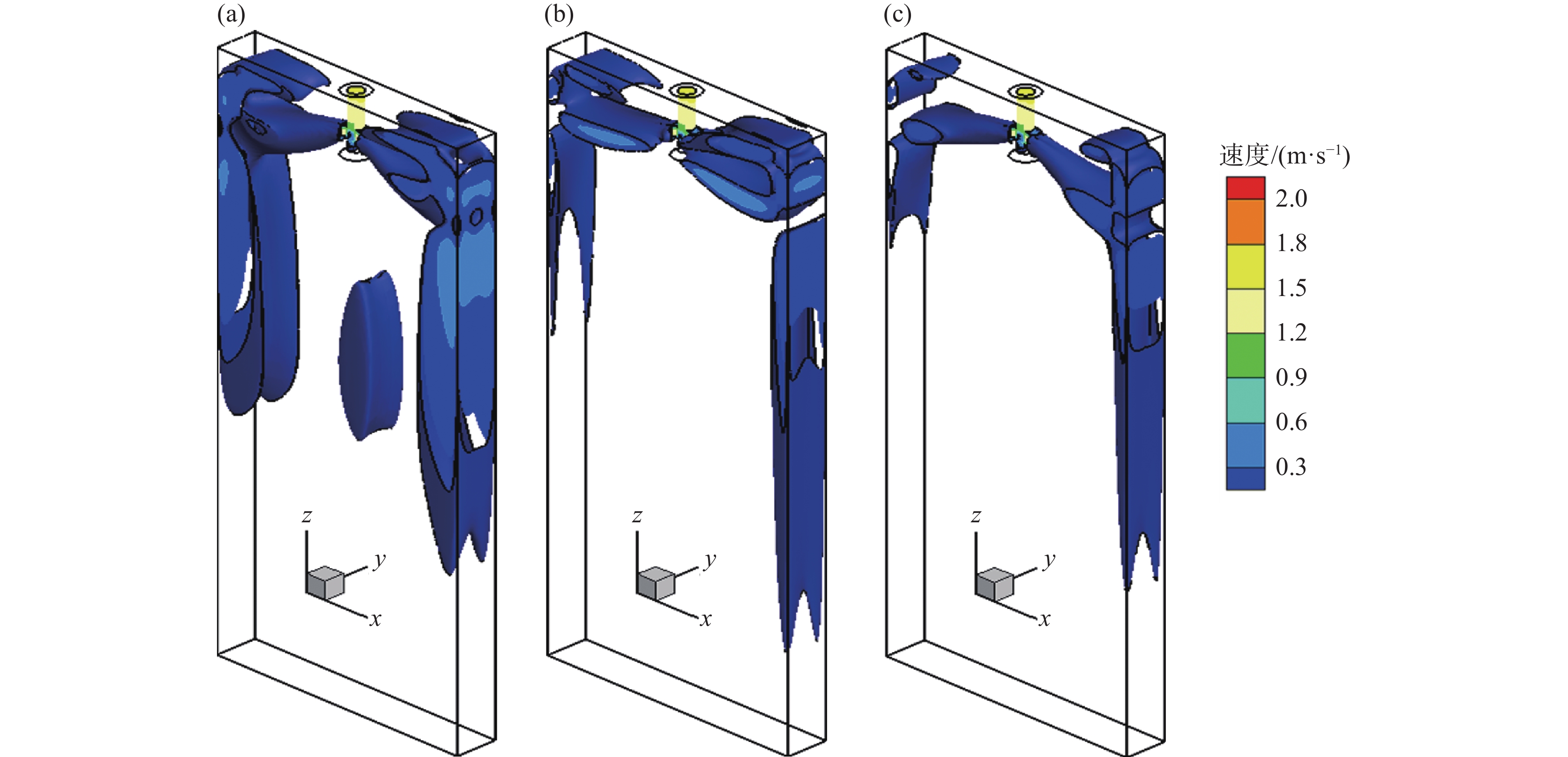
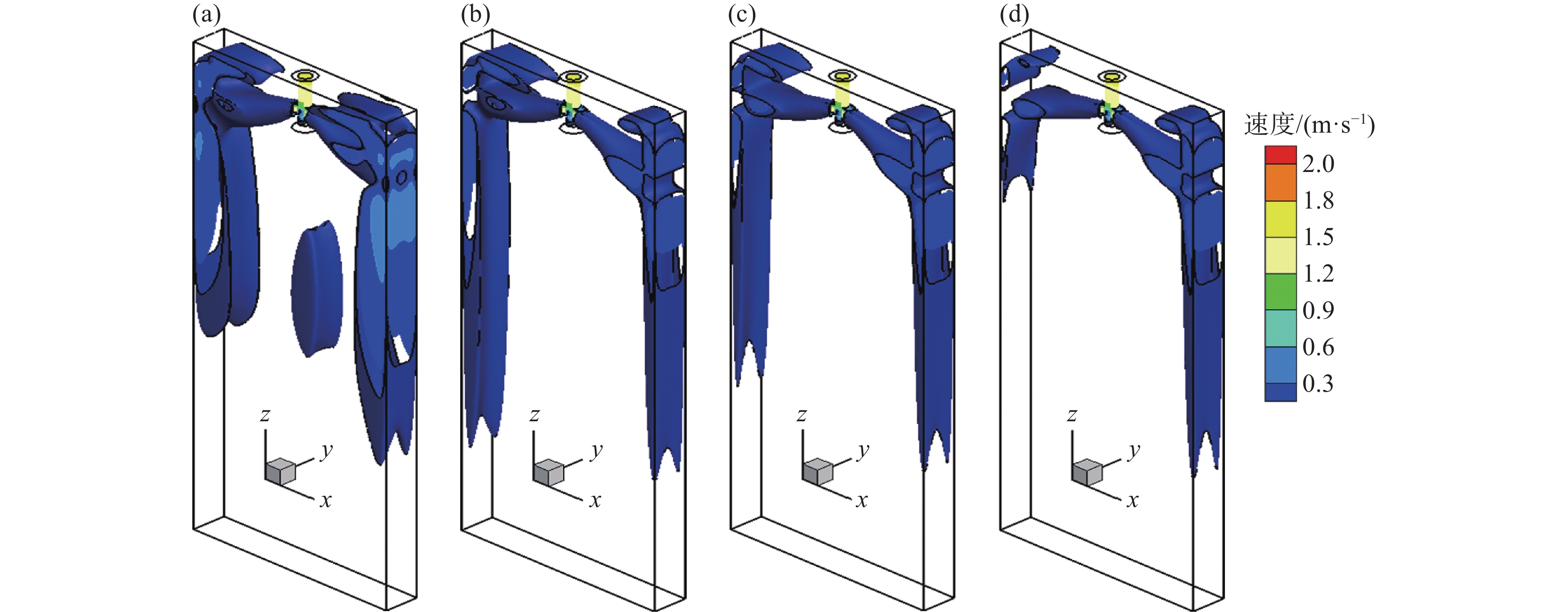
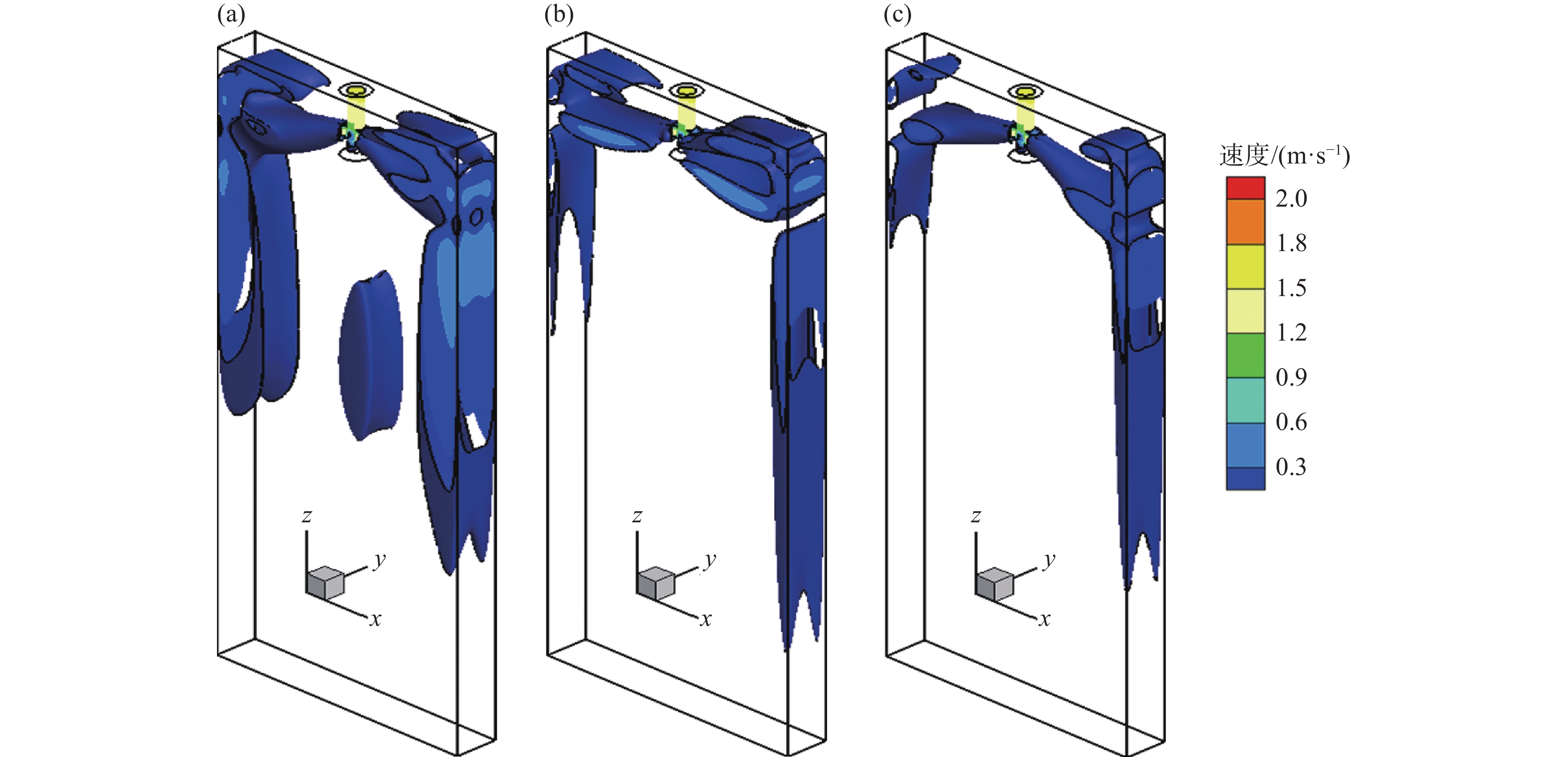
1350 A，对应立式磁极的磁场强度为0.3 T不变时，非堵塞侧结晶器上、下回流区的钢液流速得到抑制，但整个结晶器下回流区的钢液流动依然保持非均匀模式。然而，当MAC-I中水平磁极的电流强度由450 A增加至1350 A，对应立式磁极的磁场强度从0.1 T逐渐增强至0.3 T时，多区域独立可控电磁制动所产生的“L”型稳态磁场对堵塞侧结晶器内部钢液流动的控制效果逐渐增强，同时结晶器整体下部回流区的钢液流动逐渐恢复到较为对称的模式。可见，针对单侧水口堵塞导致非堵塞侧水口出流钢液流速增加的情况，采用多区域独立可控电磁制动技术，可分别调节MAC-I和MAC-II磁极的磁场强度，实现分区域控制结晶器内部钢液流动，从而改善流场的对称性，并减少因水口堵塞引起的流动不对称现象。图5为单侧水口发生25%堵塞时，结晶器内钢液流速高于0.2 m/s的等值面分布图。由图5可见，未施加电磁制动时，结晶器内上回流区、下回流区以及水口射流冲击区的钢液流速高于0.2 m/s的等值面分布范围较大。尤其是非堵塞侧结晶器内的钢液流动尤为剧烈，钢液射流对结晶器壁面的冲击速度最大值达到0.36 m/s。施加多区域独立可控电磁制动后，在保持MAC-II中水平磁极的电流强度为
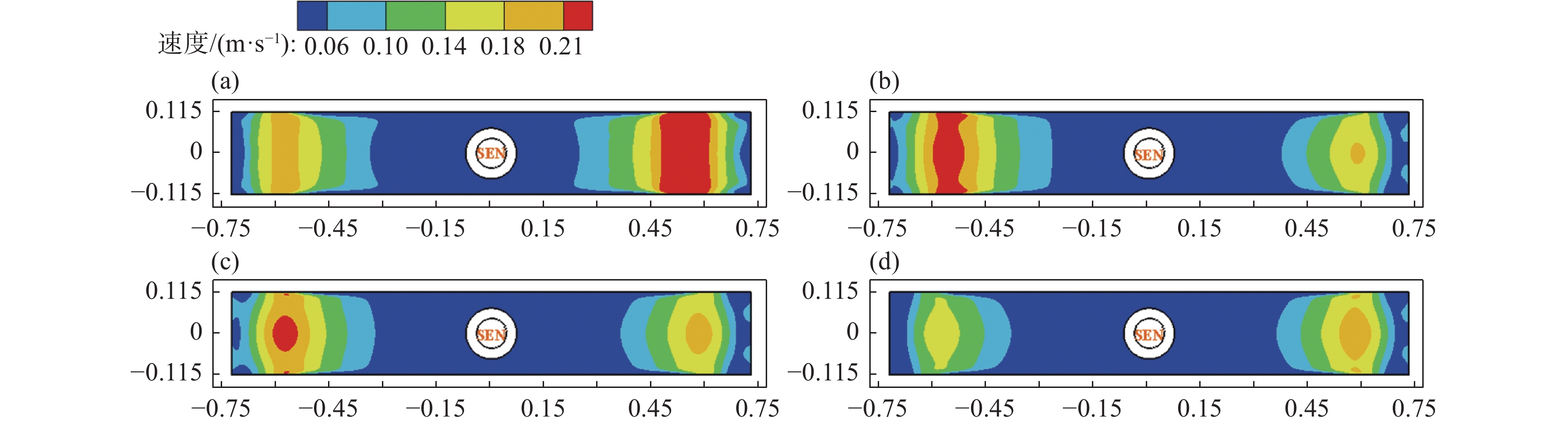
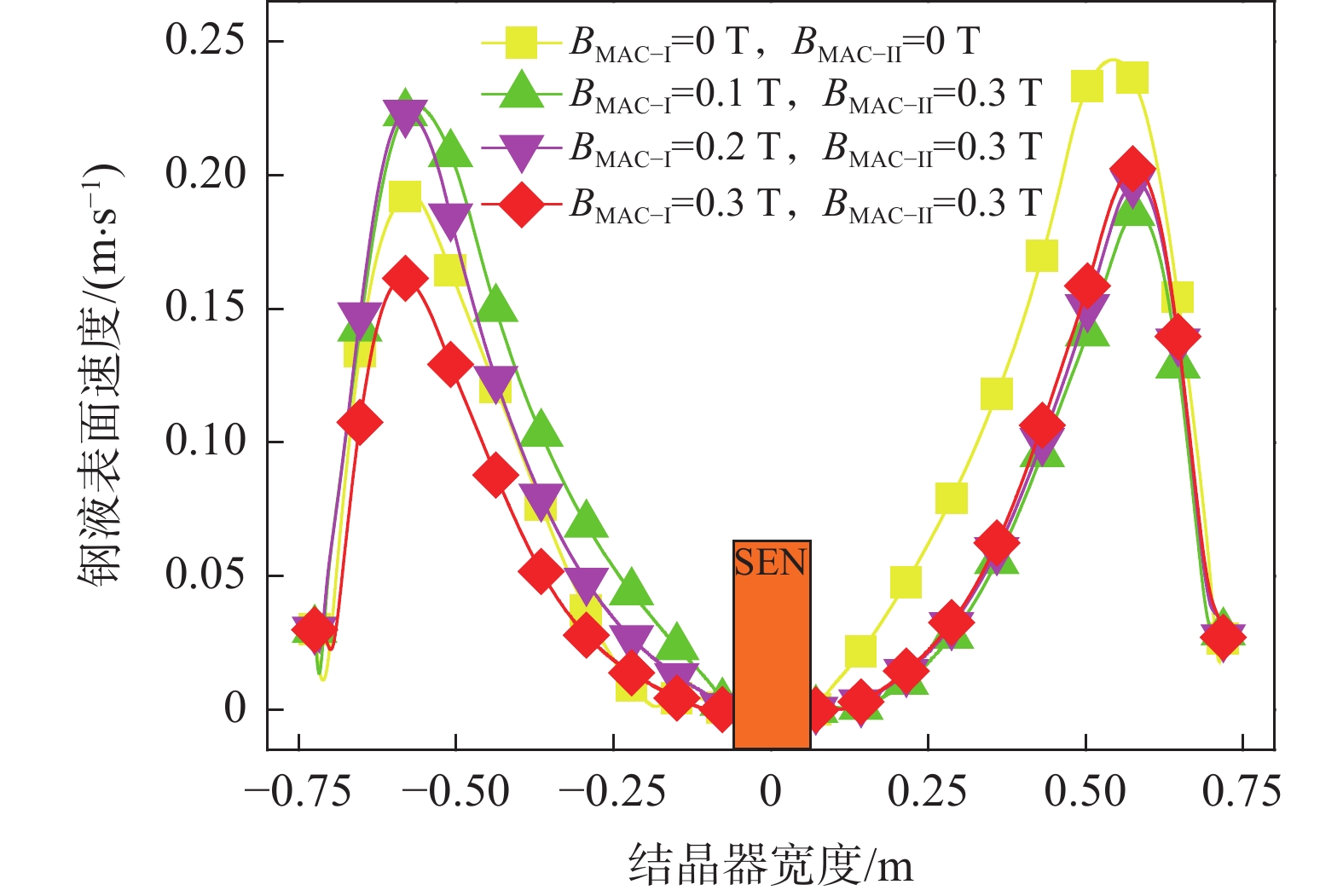
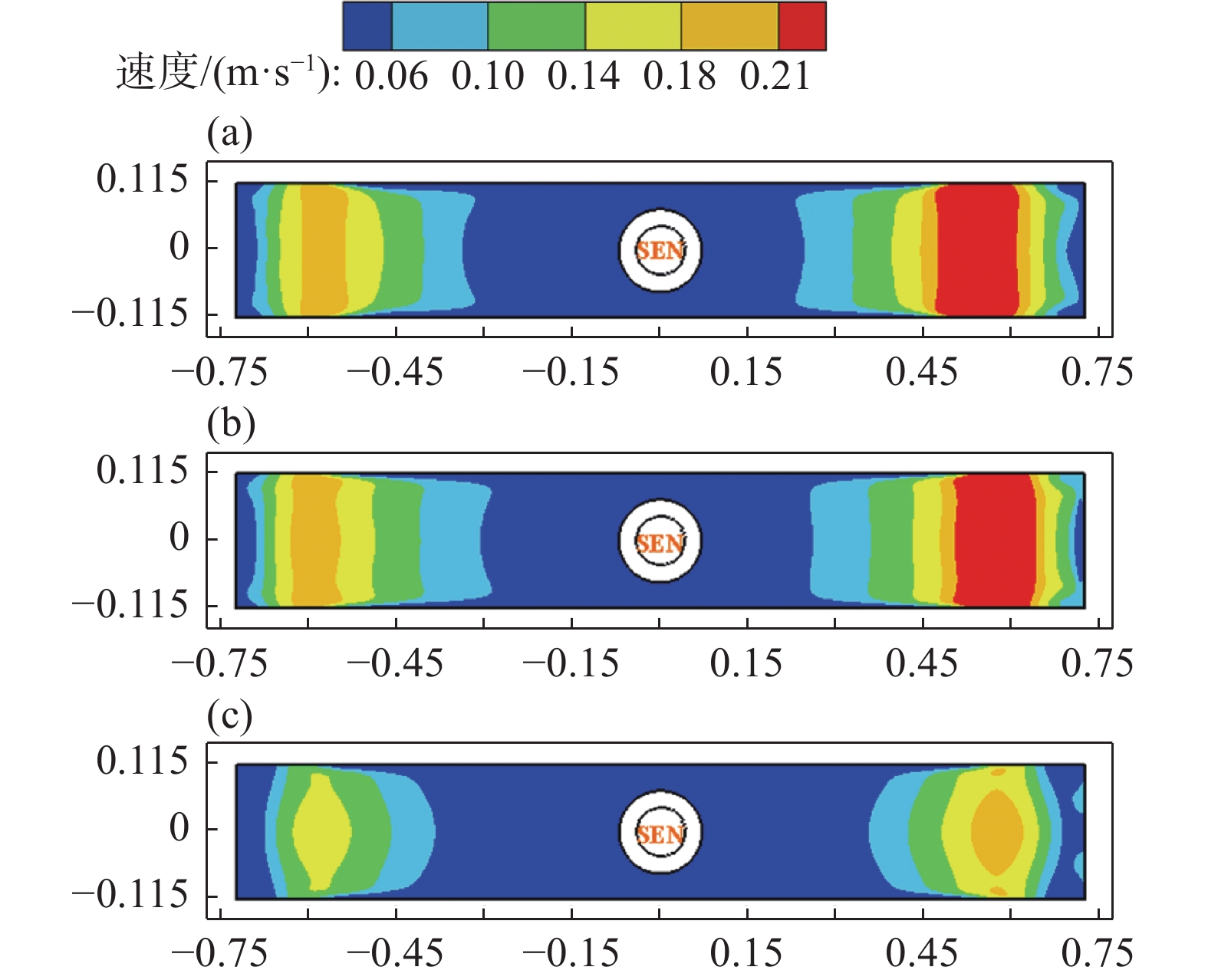
1350 A，对应立式磁极的磁场强度为0.3 T不变的情况下，通入MAC-I中水平磁极的电流强度由450 A增加至1350 A，对应立式磁极的磁场强度从0.1 T增强至0.3 T的过程中，堵塞侧钢液射流对结晶器壁面的冲击显著减弱，且回流区钢液流动被有效抑制，同时非堵塞侧水口射流冲击区的钢液流速高于0.2 m/s的等值面分布显著降低，且钢液射流冲击壁面的速度最大值降低至0.27 m/s。
图 5 多区域独立可控电磁制动结晶器内钢液速度等直面图Figure 5. Isosurface diagram of velocity in the mold with MAC-EMBr(a) BMAC-I=BMAC-II=0 T；(b) BMAC-I=0.1 T，BMAC-II=0.3 T；(c) BMAC-I=0.2 T，BMAC-II=0.3 T；(d) BMAC-I=BMAC-II=0.3 T图6、7分别为结晶器内钢液表面速度分布云图和钢液表面中心线上(x = ‒0.725～0.725 m，y = 0 m，z = 0 m)速度变化趋势图。由图6、7可知，由于单侧水口发生堵塞，非堵塞侧钢液流速急剧提升，导致未施加电磁制动时，非堵塞侧钢液表面流速明显高于堵塞侧，两者之间钢液速度最大差值可达0.05 m/s。与未施加电磁制动时相比，当MAC-I中水平磁极的电流强度由450 A增加至900 A，对应立式磁极的磁场强度由0.1 T增加至0.2 T时，所产生的电磁力并不能有效地抑制堵塞侧水口出流钢液的流动，导致钢液表面流速最大值由0.19 m/s增加至0.22 m/s。然而，当通入MAC-I和MAC-II中水平磁极的电流强度为
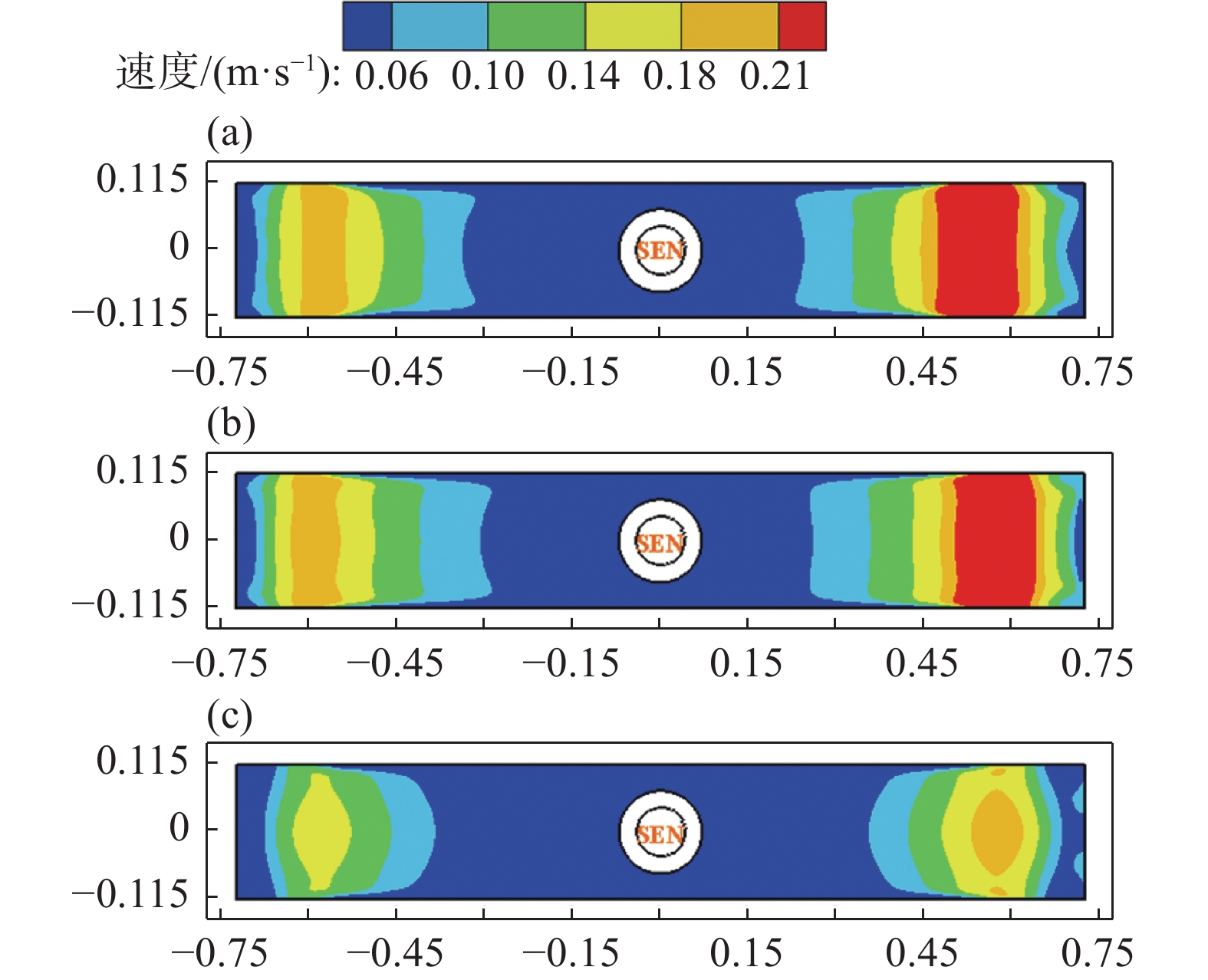
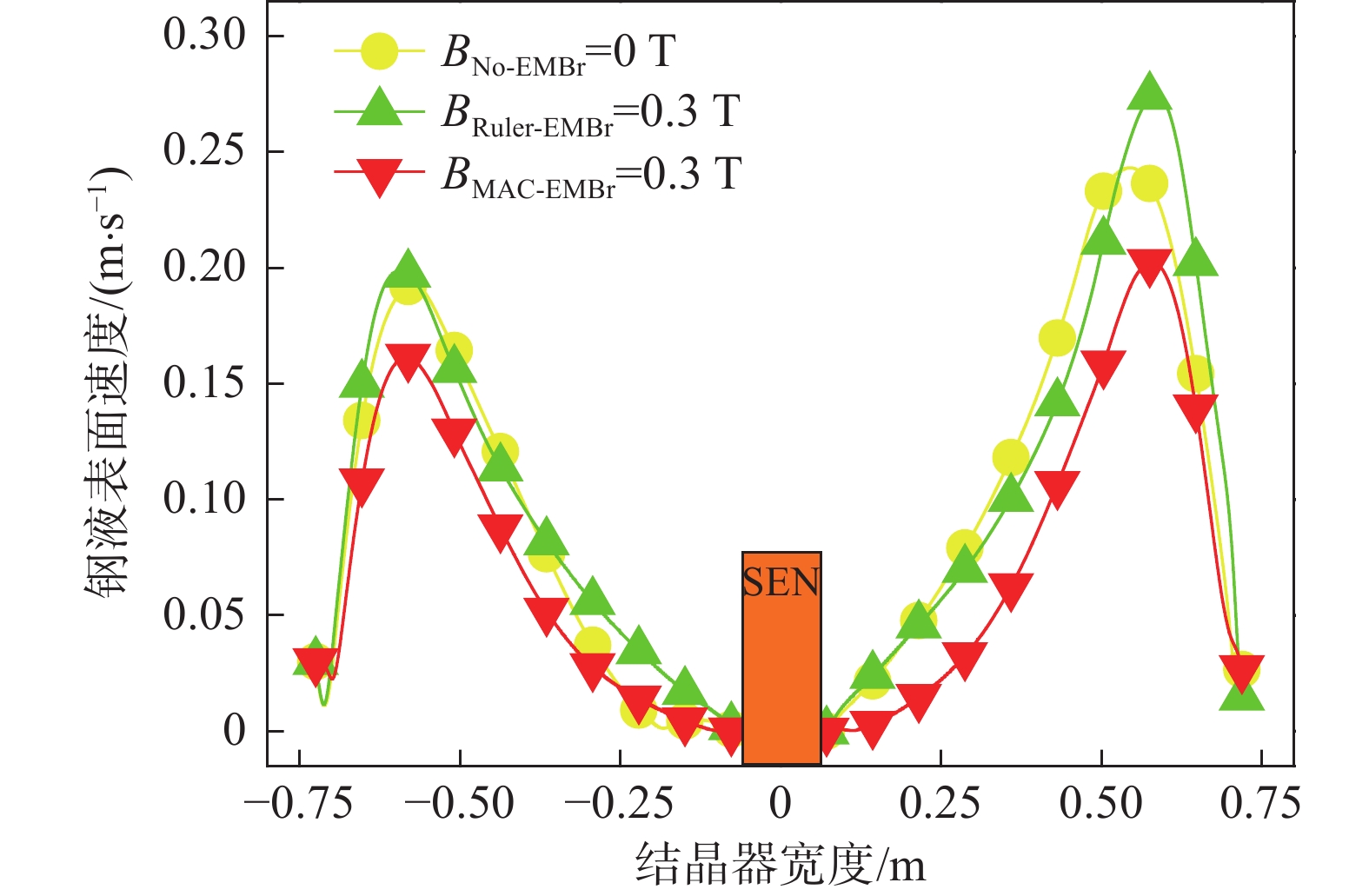
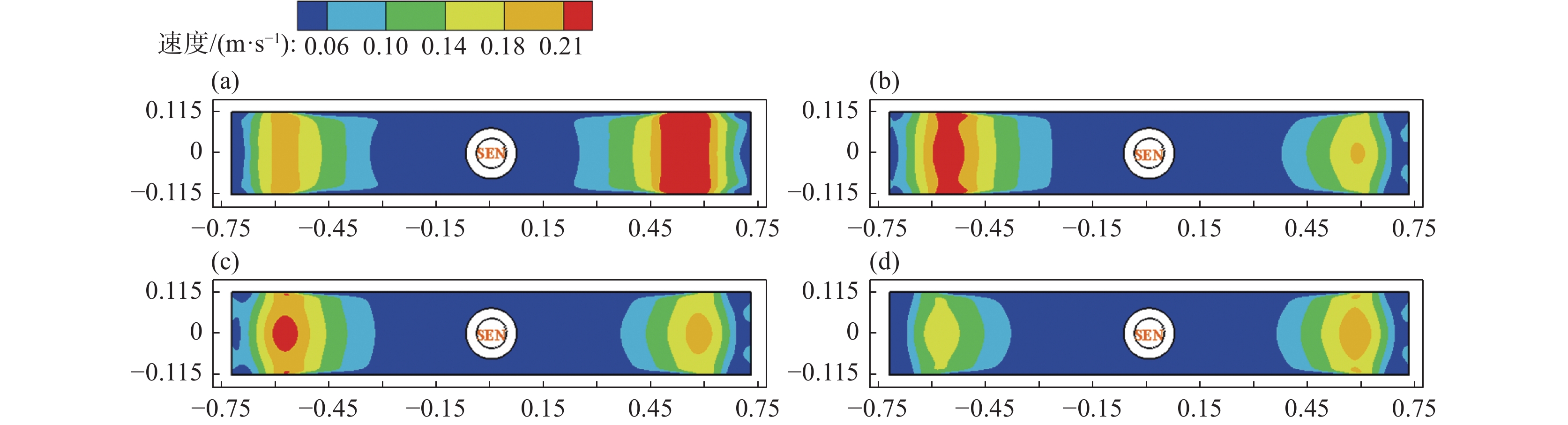
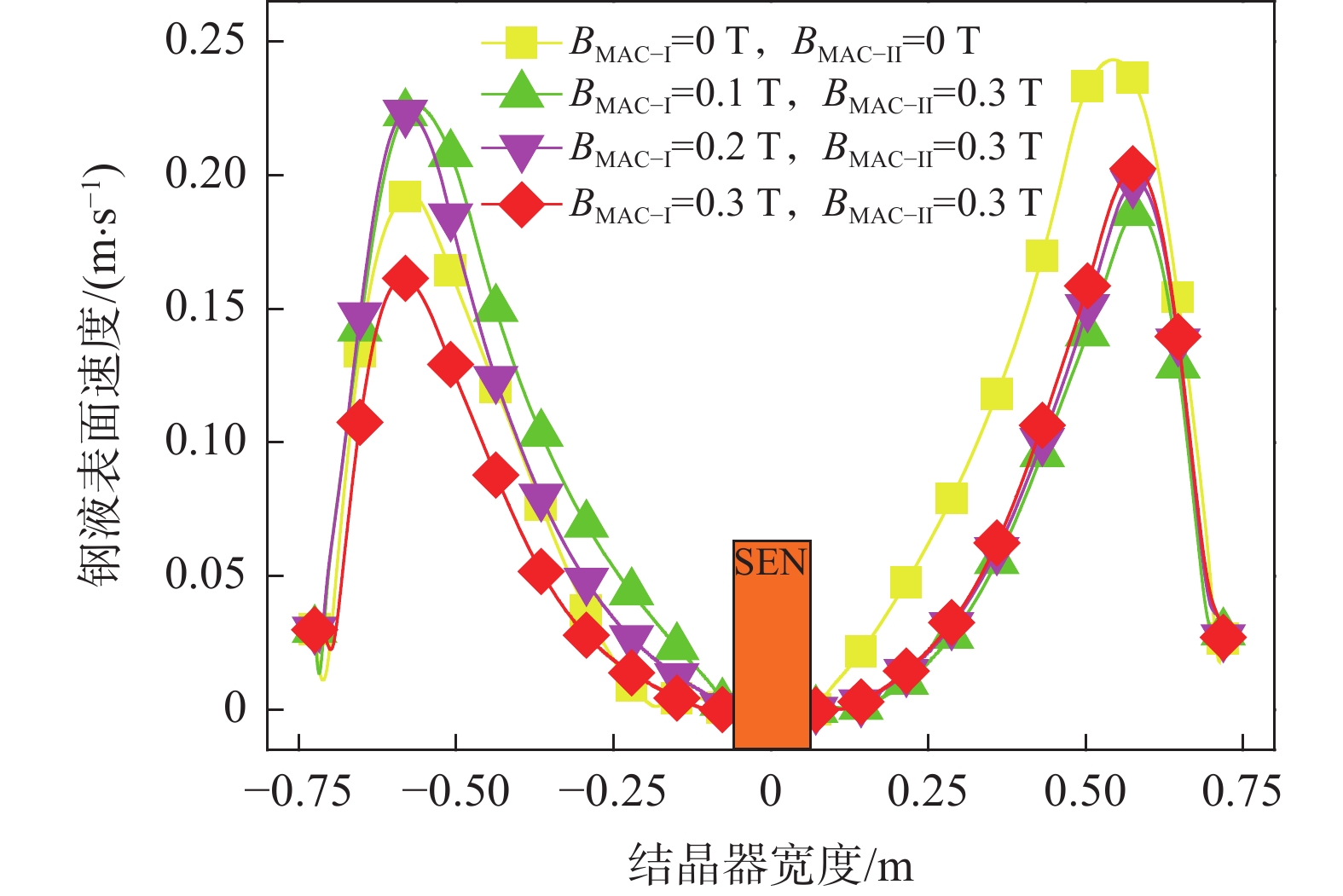
1350 A，立式磁极的磁场强度均达到0.3 T时，结晶器内钢液表面流速得到显著抑制，堵塞侧和非堵塞侧钢液表面流速最大值分别降低至0.16 m/s和0.20 m/s，两者间的最大速度差缩小至0.04 m/s，相比于未施加电磁制动时降低了20%。此结果再次证明采用多区域独立可控电磁制动技术，可优化流场结构，改善因水口阻塞而引发的流动不均衡问题。
图 6 多区域独立可控电磁制动结晶器内钢液表面速度分布云图Figure 6. Nephogram of surface velocity in the mold with MAC-EMBr(a) BMAC-I=BMAC-II=0 T；(b) BMAC-I=0.1 T，BMAC-II=0.3 T；(c) BMAC-I=0.2 T，BMAC-II=0.3 T；(d) BMAC-I=BMAC-II=0.3 T4.3 多区域独立可控电磁制动结晶器内渣金界面波动特征
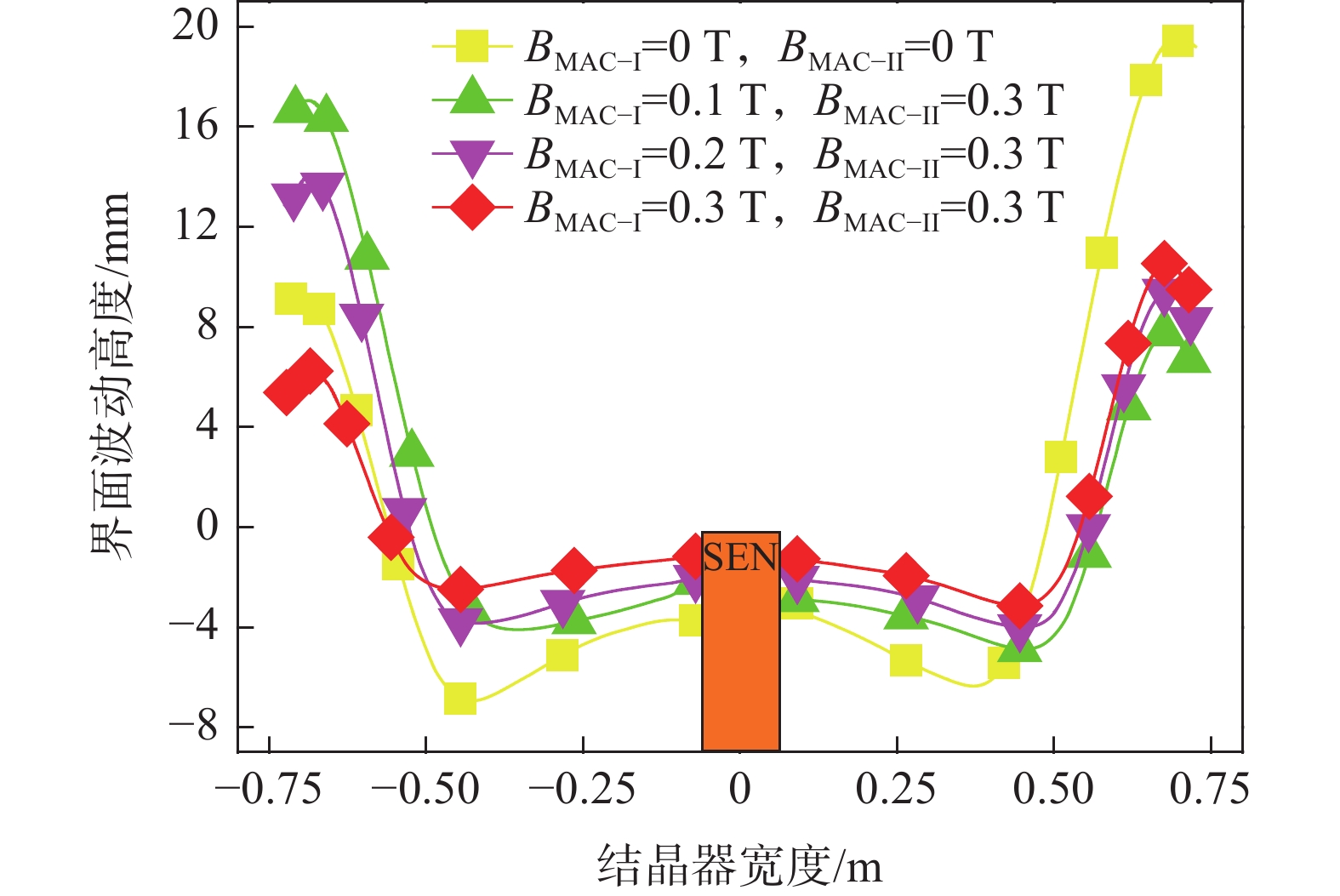
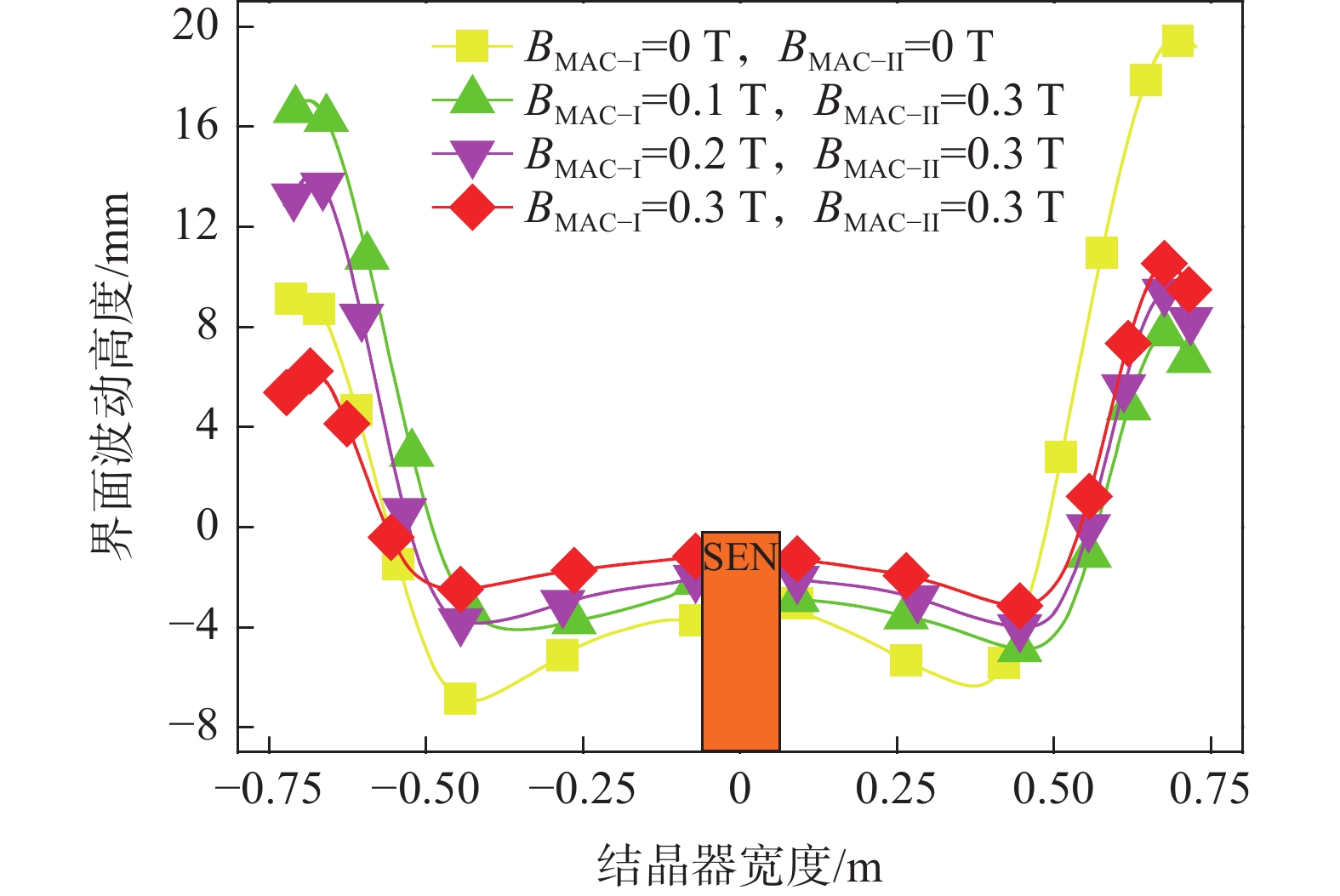
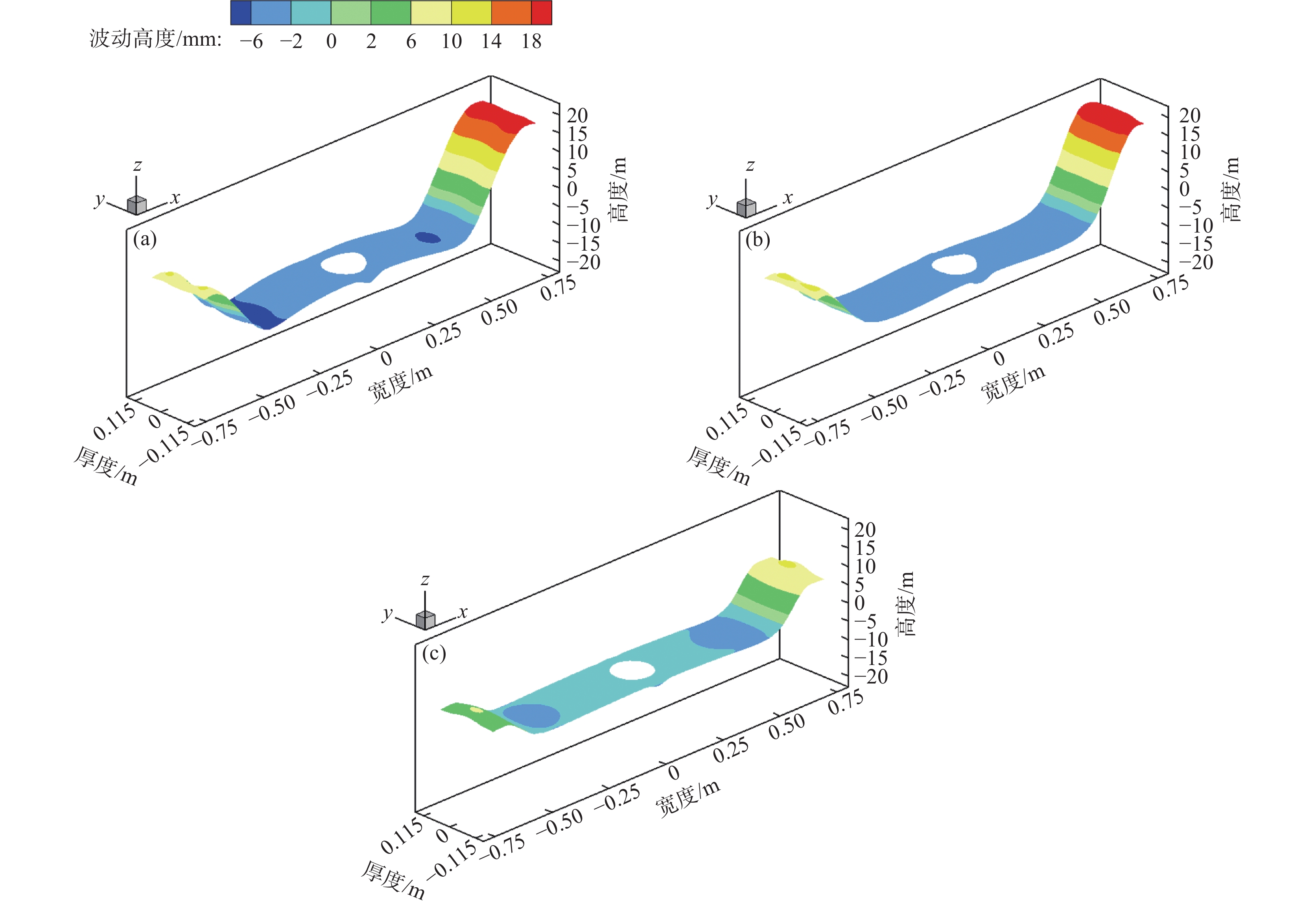
图8、9分别为结晶器内渣金界面三维波动云图和界面中心线上波高变化趋势图。其中，钢液体积分数Ф为0.5，渣金界面波动时间为120 s。由图8、9可知，未施加电磁制动时，单侧水口发生堵塞后，非堵塞侧结晶器内渣金界面呈现出显著且剧烈的波动，此时界面最大波高达到25.8 mm，堵塞侧和非堵塞侧两者间的最大波高相差9.7 mm。施加多区域独立可控电磁制动后，在MAC-II中水平磁极的电流强度保持
1350 A，立式磁极的磁场强度维持0.3 T不变的情况下，当MAC-I中水平磁极的电流强度由450 A增加至1350 A，立式磁极的磁场强度由0.1 T逐渐增强至0.3 T时，所产生的电磁力可有效改善因水口堵塞带来的渣金界面波动不稳定情况。此时堵塞侧和非堵塞侧界面波高最大值分别降低至8.7和13.7 mm，两者间的最大波动高度差减小至5.0 mm，相比于未施加电磁制动时显著降低了48.5%。可见，在单侧水口发生25%堵塞的情况下，当通入MAC-I和MAC-II中水平磁极的电流强度为1350 A，对应立式磁极的磁场强度达到0.3 T时，在结晶器窄面形成的立式稳态磁场不仅能够有效减少因非堵塞侧钢液流速过快而导致的液面波动加剧现象，还能够显著改善因水口阻塞造成的界面波动不均衡问题。
图 7 多区域独立可控电磁制动结晶器内钢液表面速度分布Figure 7. Surface velocity distribution in the mold with MAC-EMBr
图 8 多区域独立可控电磁制动结晶器内渣金界面波动云图Figure 8. Nephogram of steel slag interface fluctuation in the mold with MAC-EMBr(a) Bleft = Bright = 0.0 T；(b) Bleft = 0.1 T，Bright = 0.3 T；(c) Bleft = 0.2 T，Bright = 0.3 T；(d) Bleft = 0.3 T，Bright = 0.3 T
图 9 多区域独立可控电磁制动结晶器内渣金界面波动高度Figure 9. Fluctuation height of steel slag interface in the mold with MAC-EMBr4.4 多区域与全幅一段电磁制动结晶器内钢液流动效果评价
图10为有、无电磁制动作用下，结晶器宽面中心截面钢液速度云图和流线图。其中，全幅一段电磁制动和多区域独立可控电磁制动所施加的磁场强度为0.3 T，全幅一段电磁制动和多区域独立可控电磁制动装置的水平磁极上沿分别距离结晶器顶部255 mm和500 mm。由图10可见，未施加电磁制动时，由于水口发生25%堵塞，非堵塞侧钢液流动加剧，导致上、下回流区钢液流动分布不均匀。施加全幅一段电磁制动后，其产生的稳恒磁场能够有效抑制下回流区的钢液流动，并改善该区域内钢液流动的不均匀性。然而，全幅一段电磁制动在结晶器高度方向上的作用范围有限，上回流钢液仍以较大的速度向液面冲击，反而不利于维持液面的稳定性。相比之下，施加多区域独立可控电磁制动后，在结晶器窄面形成的立式稳态磁场能够有效控制上返流流动，进而减少因非堵塞侧钢液流速过快而导致的液面波动和卷渣问题。不仅如此，在MAC-I和MAC-II磁极的共同作用下，在结晶器宽面形成的稳态磁场能够有效抑制结晶器内下回流区的钢液流动，并且能够改善因水口堵塞导致的结晶器内钢液流态畸变，从而促使钢液流动状态趋向于对称分布。
图 10 结晶器宽面中心截面钢液速度分布(a) 无磁场；(b) 全幅一段电磁制动；(c) 多区域独立可控电磁制动Figure 10. Velocity distribution in the central section of wide surface in the mold under different braking conditions图11为单侧水口堵塞25%时，结晶器内钢液流速高于0.2 m/s的等值面分布图。由图11可见，与未施加电磁制动相比，施加全幅一段电磁制动后，其产生的阻尼效应能够有效抑制钢液射流向结晶器窄侧壁的冲击，使得冲击区内的钢液流速最大值降低至0.31 m/s。然而，这种改变导致钢液射流对结晶器宽面两侧的冲击增强。特别是单侧水口发生堵塞时，非堵塞侧钢液射流对结晶器宽面的最大冲击速度显著增加至0.45 m/s，相比于未施加电磁制动时增加了25%。相比之下，施加多区域独立可控电磁制动后，在MAC-I和MAC-II磁极的共同作用下，钢液射流向结晶器宽面的最大冲击速度显著降低至0.28 m/s，相比于未施加电磁制动时降低了22.2%。可见，当水口发生堵塞时，施加多区域独立可控电磁制动能够有效防止因非堵塞侧水口射流流动增强而对结晶器壁面造成过度的冲刷。
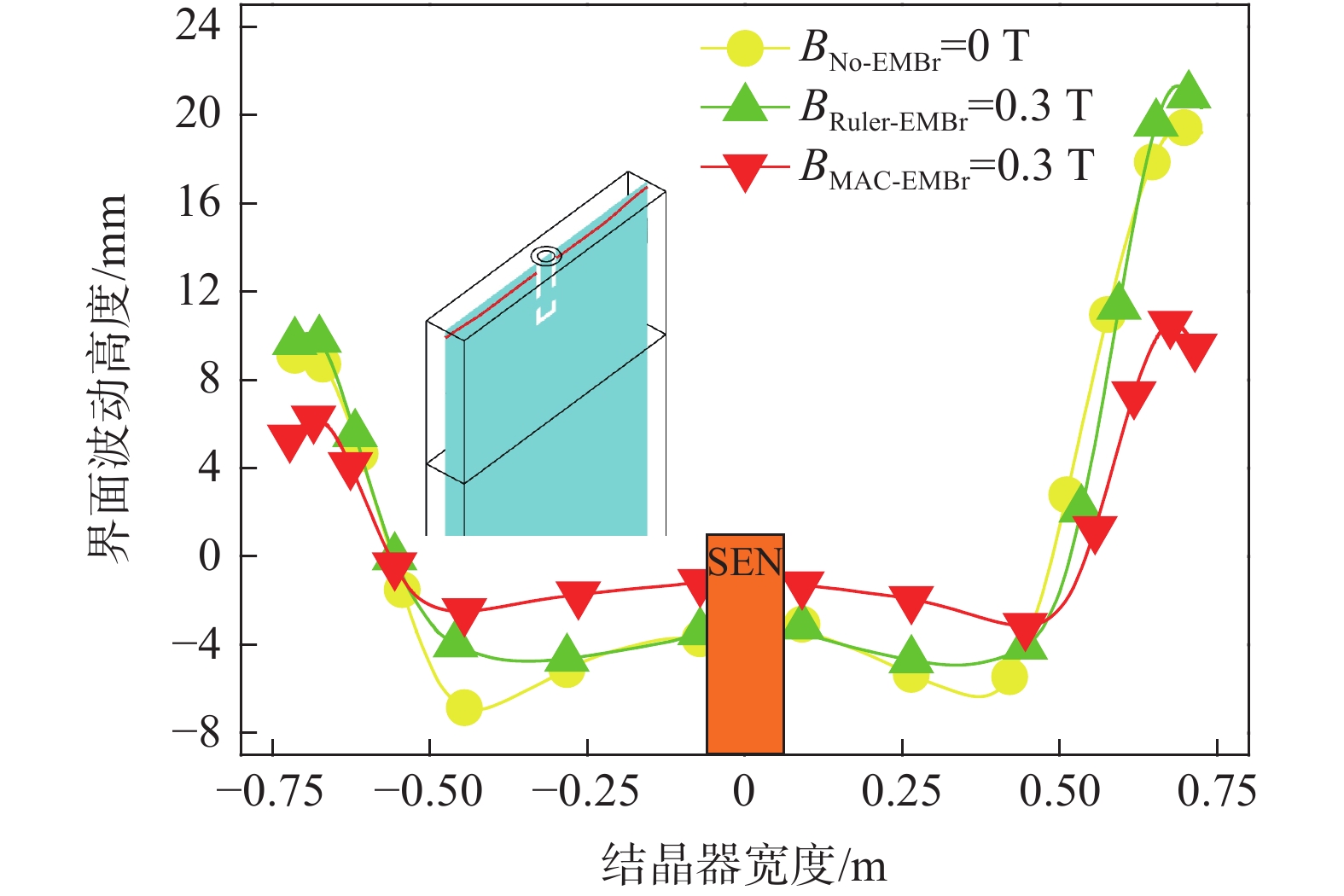
图 11 结晶器内钢液速度等直面图(a) 无磁场；(b) 全幅一段电磁制动；(c) 多区域独立可控电磁制动Figure 11. Isosurface diagram of velocity in the mold under different braking conditions图12、13分别为有、无电磁制动作用下，结晶器内钢液表面速度分布云图和钢液表面中心线上速度变化趋势图。由图12、13可知，当单侧水口发生25%堵塞时，与未施加电磁制动相比，尽管全幅一段电磁制动施加的磁场强度达到0.3 T，但水平磁极所产生的稳恒磁场对上回流区钢液的流动控制效果并不显著，此时堵塞侧和非堵塞侧钢液表面流速最大值分别增加至0.20 m/s和0.28 m/s，两者间的最大速度差增加至0.08 m/s。相较于全幅一段电磁制动，当多区域独立可控电磁制动MAC-I和MAC-II磁极的磁场强度同样达到0.3 T时，此时堵塞侧和非堵塞侧两者间的钢液表面最大速度差显著缩小至0.04 m/s。可见，采用多区域独立可控电磁制动技术更利于控制因水口堵塞而引发的偏流。
图 12 结晶器内钢液表面速度分布云图(a) 无磁场；(b) 全幅一段电磁制动；(c) 多区域独立可控电磁制动Figure 12. Nephogram of surface velocity in the mold under different braking conditions4.5 多区域与全幅一段电磁制动结晶器内渣金界面波动效果评价
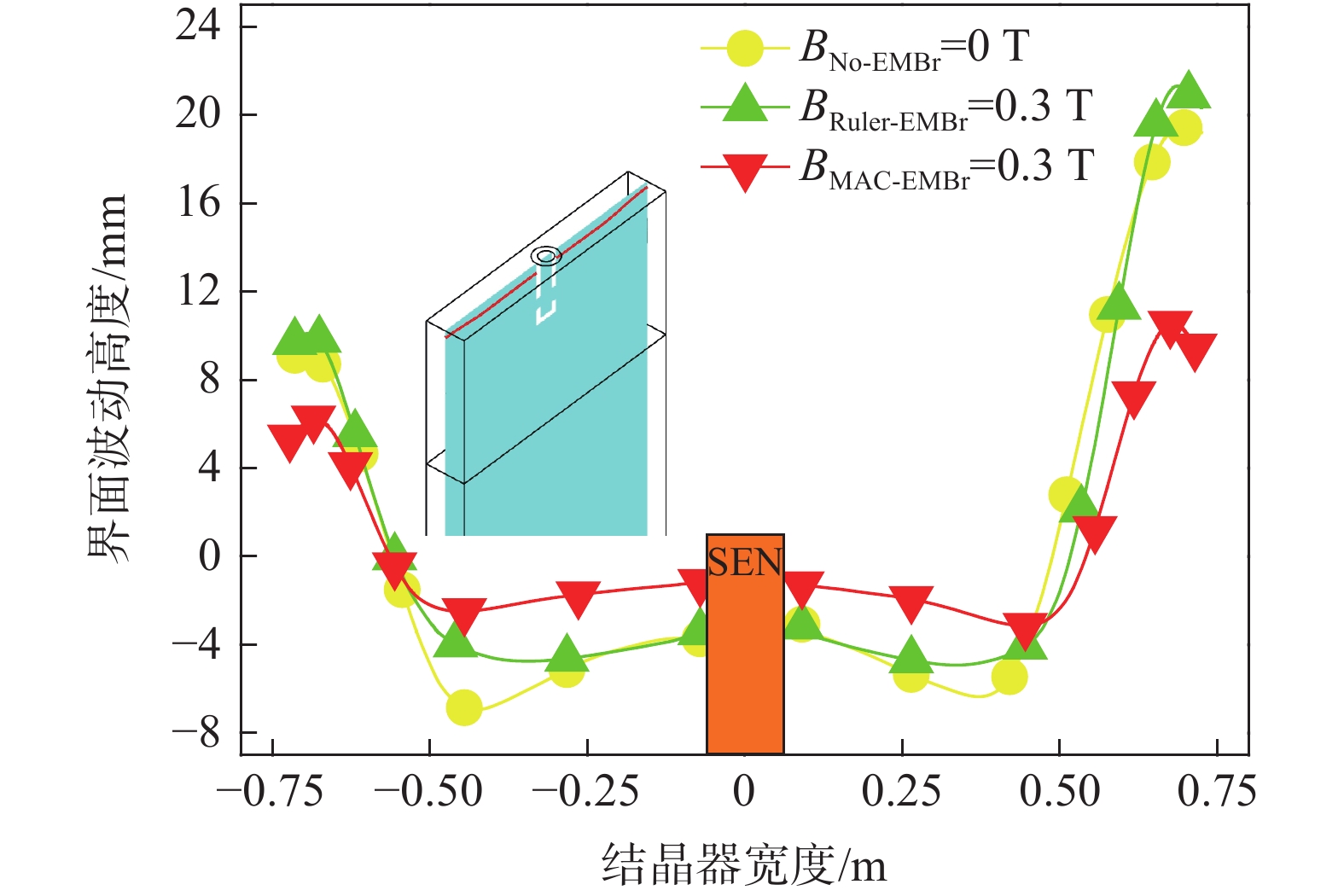
图14和图15分别为有、无电磁制动作用下，结晶器内渣金界面三维波动云图和界面中心线上波高变化趋势图。结合先前图12和图13的分析结果，图14和图15的结果再次证明施加全幅一段电磁制动并不利于抑制上回流区的钢液流速。特别是在单侧水口发生堵塞后，非堵塞侧结晶器内的渣金界面呈现出剧烈波动，此时界面最大波高达到26.2 mm，堵塞侧和非堵塞侧两者间的最大波高相差11.4 mm，相比于未施加电磁制动时反而增加了17.5%。相较于全幅一段电磁制动，多区域独立可控电磁制动在结晶器窄面形成的立式稳态磁场能够显著改善因水口阻塞造成的界面波动不均衡问题，当MAC-I和MAC-II磁极的磁场强度达到0.3 T时，非堵塞侧界面波高最大值显著降低至13.7 mm，相比于施加全幅一段电磁制动时的情况显著降低了47.7%。
图 14 结晶器内渣金界面波动云图(a) 无磁场；(b) 全幅一段电磁制动；(c) 多区域独立可控电磁制动Figure 14. Nephogram of steel slag interface fluctuation in the mold under different braking conditions5. 结论
1)施加多区域独立可控电磁制动，其产生的稳恒磁场可控制结晶器上回流区、水口射流冲击区以及弯月面区内的钢液流动。在单侧水口发生25%堵塞的情况下，当MAC-I和MAC-II中水平磁极的电流强度为
1350 A，对应立式磁极的磁场强度均达到0.3 T时，堵塞侧和非堵塞侧两者间的钢液表面流速最大速度差缩小至0.04 m/s，相比于未施加电磁制动时降低了20%。2)在MAC-I和MAC-II磁极的共同作用下，施加多区域独立可控电磁制动可以减弱水口出流钢液对结晶器壁面的冲击。在单侧水口发生25%堵塞的情况下，当MAC-I和MAC-II磁极的磁场强度均达到0.3 T时，非堵塞侧钢液射流向结晶器壁面的最大冲击速度与未施加电磁制动时相比显著降低了22.2%。
3)相较于全幅一段电磁制动装置，采用多区域独立可控电磁制动装置能够显著改善因水口阻塞造成的界面波动不均衡问题。在单侧水口发生25%堵塞的情况下，当MAC-I和MAC-II磁极的磁场强度均达到0.3 T时，非堵塞侧界面波高最大值显著降低至13.7 mm，相比于施加全幅一段电磁制动时的情况显著降低了47.7%。
-
图 2 试验测量和数值模拟结晶器内液面波动结果
(a) 试验测量结果；(b) 试验和模拟比对结果
Figure 2. Experimental measurement and numerical simulation of level fluctuation heights in the mold
图 3 多区域独立可控电磁制动结晶器内磁场强度分布
(a) 结晶器内磁场强度；(b) 沿结晶器高度方向宽面中心截面磁场强度
Figure 3. Distribution of magnetic field intensity in the mold with MAC-EMBr
图 4 多区域独立可控电磁制动结晶器宽面中心截面钢液速度分布
Figure 4. Velocity distribution in the central section of wide surface in the mold with MAC-EMBr
(a) BMAC-I=BMAC-II=0 T；(b) BMAC-I=0.1 T，BMAC-II=0.3 T；(c) BMAC-I=0.2 T，BMAC-II=0.3 T；(d) BMAC-I=BMAC-II=0.3 T
图 5 多区域独立可控电磁制动结晶器内钢液速度等直面图
Figure 5. Isosurface diagram of velocity in the mold with MAC-EMBr
(a) BMAC-I=BMAC-II=0 T；(b) BMAC-I=0.1 T，BMAC-II=0.3 T；(c) BMAC-I=0.2 T，BMAC-II=0.3 T；(d) BMAC-I=BMAC-II=0.3 T
图 6 多区域独立可控电磁制动结晶器内钢液表面速度分布云图
Figure 6. Nephogram of surface velocity in the mold with MAC-EMBr
(a) BMAC-I=BMAC-II=0 T；(b) BMAC-I=0.1 T，BMAC-II=0.3 T；(c) BMAC-I=0.2 T，BMAC-II=0.3 T；(d) BMAC-I=BMAC-II=0.3 T
图 7 多区域独立可控电磁制动结晶器内钢液表面速度分布
Figure 7. Surface velocity distribution in the mold with MAC-EMBr
图 8 多区域独立可控电磁制动结晶器内渣金界面波动云图
Figure 8. Nephogram of steel slag interface fluctuation in the mold with MAC-EMBr
(a) Bleft = Bright = 0.0 T；(b) Bleft = 0.1 T，Bright = 0.3 T；(c) Bleft = 0.2 T，Bright = 0.3 T；(d) Bleft = 0.3 T，Bright = 0.3 T
图 9 多区域独立可控电磁制动结晶器内渣金界面波动高度
Figure 9. Fluctuation height of steel slag interface in the mold with MAC-EMBr
图 10 结晶器宽面中心截面钢液速度分布
(a) 无磁场；(b) 全幅一段电磁制动；(c) 多区域独立可控电磁制动
Figure 10. Velocity distribution in the central section of wide surface in the mold under different braking conditions
图 11 结晶器内钢液速度等直面图
(a) 无磁场；(b) 全幅一段电磁制动；(c) 多区域独立可控电磁制动
Figure 11. Isosurface diagram of velocity in the mold under different braking conditions
图 12 结晶器内钢液表面速度分布云图
(a) 无磁场；(b) 全幅一段电磁制动；(c) 多区域独立可控电磁制动
Figure 12. Nephogram of surface velocity in the mold under different braking conditions
图 14 结晶器内渣金界面波动云图
(a) 无磁场；(b) 全幅一段电磁制动；(c) 多区域独立可控电磁制动
Figure 14. Nephogram of steel slag interface fluctuation in the mold under different braking conditions
表 1 板坯结晶器计算参数
Table 1. Computational parameters of slab mold
铸坯断面/（mm×mm） 结晶器长度/mm 结晶器计算域/mm 水口双侧孔尺寸/mm 水口浸入深度/mm 水口内径/mm 拉坯速度/(m∙min−1) 1450 ×230800 4000 65×80 170 80 1.8 钢液密度/(kg∙m−3) 钢液黏度/(Pa∙s) 钢液电导率/(S∙m−1) 钢液磁导率/(H∙m−1) 液渣密度/(kg∙m−3) 表面张力/(N∙m−1) 磁场强度/T 7020 0.0062 7.14×105 1.26×106 3500 1.2 0.1 0.2 0.3 
下载: 导出CSV
表 2 计算域内不同网格节点数的误差统计结果
Table 2. Statistic results of error with different grid node numbers in the computational domain
网格 M1 M2 M3 网格节点数 490,000 735,000 1,102,500 $ {h_{{{\text{M}}_i}}} $ 25.8 25.2 24.9 $ {\delta _h} = {{\left| {{h_{{{\text{M}}_i}}} - {h_{{{\text{M}}_1}}}} \right|} \mathord{\left/ {\vphantom {{\left| {{h_{{{\text{M}}_i}}} - {h_{{{\text{M}}_1}}}} \right|} {{h_{{{\text{M}}_1}}}}}} \right. } {{h_{{{\text{M}}_1}}}}} $ 0 2.3% 3.5% 注：表中h为渣金界面波动高度最大值，即波峰与波谷间的垂直距离，mm；δh为渣金界面波动高度的相对误差，%。
下载: 导出CSV
-
[1] BAO Y, LI Z, ZHANG L, et al. Asymmetric flow control in a slab mold through a new type of electromagnetic field arrangement[J]. Processes, 2021,9(11):1988-2000. doi: 10.3390/pr9111988 [2] WANG T, LI K, LI S, et al. Asymmetric flow behavior of molten steel in thin slab continuous casting mold[J]. Metall. Mater. Trans. B, 2023,54(3):3542-3553. [3] WANG Z, LIU J, CUI H, et al. Effect of SEN asymmetric clogging on mold level fluctuation and mold slag distribution during continuous casting[J]. Metall. Mater. Trans. B, 2024,55(4):2932-2947. doi: 10.1007/s11663-024-03156-5 [4] REN Z M, LEI Z S, LI C J, et al. New study and development on electromagnetic field technology in metallurgical processes[J]. Acta Metallurgica Sinica, 2020,56(4):583-600. (任忠鸣, 雷作胜, 李传军, 等. 电磁冶金技术研究新进展[J]. 金属学报, 2020,56(4):583-600.REN Z M, LEI Z S, LI C J, et al. New study and development on electromagnetic field technology in metallurgical processes[J]. Acta Metallurgica Sinica, 2020, 56（4）: 583-600. [5] ZHU M Y. Some considerations for new generation of high-efficiency continuous casting technology development[J]. Iron and steel, 2019,54(8):21-36. (朱苗勇. 新一代高效连铸技术发展思考[J]. 钢铁, 2019,54(8):21-36.ZHU M Y. Some considerations for new generation of high-efficiency continuous casting technology development[J]. Iron and steel, 2019, 54（8）: 21-36. [6] LUO S, YANG Y W, WANG W L, et al. Development of electromagnetic flow control technology for high speed casting mold[J]. Journal of Materials and Metallurgy, 2023,22(1):1-22. (罗森, 杨宇威, 王卫领, 等. 高拉速连铸结晶器电磁控流技术发展[J]. 材料与冶金学报, 2023,22(1):1-22.LUO S, YANG Y W, WANG W L, et al. Development of electromagnetic flow control technology for high speed casting mold[J]. Journal of Materials and Metallurgy, 2023, 22（1）: 1-22. [7] XU L, PEI Q W, LI YANG, et al. Investigation of multiphase transport behaviors in a FTSR mold during electromagnetic continuous casting process[J]. Iron Steel Vanadium Titanium, 2023,44(4):125-134. (许琳, 裴群武, 李阳, 等. 电磁连铸过程FTSR结晶器多相传输行为的研究[J]. 钢铁钒钛, 2023,44(4):125-134.XU L, PEI Q W, LI YANG, et al. Investigation of multiphase transport behaviors in a FTSR mold during electromagnetic continuous casting process[J]. Iron Steel Vanadium Titanium, 2023, 44（4）: 125-134. [8] SCHURMANN D, GLAVINIC´ I, WILLERS B, et al. Impact of the electromagnetic brake position on the flow structure in a slab continuous casting mold: An experimental parameter study[J]. Metall. Mater. Trans. B, 2020,51(1):61-78. doi: 10.1007/s11663-019-01721-x [9] XU L, PEI Q W, LI N, et al. Investigation of flow and heat transfer characteristics in CSP mold with electromagnetic braking[J]. Journal of Thermal Science and Technology, 2024,23(1):15-23. (许琳, 裴群武, 李楠, 等. 电磁制动下CSP结晶器内流动与传热特性研究[J]. 热科学与技术, 2024,23(1):15-23.XU L, PEI Q W, LI N, et al. Investigation of flow and heat transfer characteristics in CSP mold with electromagnetic braking[J]. Journal of Thermal Science and Technology, 2024, 23（1）: 15-23. [10] SARKAR S, SINGH V, AJMANI S K, et al. Effect of double ruler magnetic field in controlling meniscus flow and turbulence intensity distribution in continuous slab casting mold[J]. ISIJ Int., 2016,56(12):2181-2190. doi: 10.2355/isijinternational.ISIJINT-2016-313 [11] THOMAS B G, SINGH R, VANKA S P, et al. Effect of single-ruler electromagnetic braking (EMBr) location on transient flow in continuous casting[J]. Journal for Manufacturing Science & Production, 2015,15(1):93-104. [12] XU L, PEI Q, HAN Z, et al. Influences of the braking effect of ruler EMBr on molten steel flow and steel–slag interface fluctuation in a continuous casting mold[J]. Processes, 2023,11(1):33-49. [13] VAKHRUSHEV A, KARIMI-SIBAKI E, BOHACEK J, et al. Impact of submerged entry nozzle (SEN) immersion depth on meniscus flow in continuous casting mold under electromagnetic brake (EMBr)[J]. Metals, 2023,13(3):444-464. doi: 10.3390/met13030444 [14] LI Z, ZHANG L T, MA D Z, et al. A narrative review: the electromagnetic field arrangement and the “braking” effect of electromagnetic brake (EMBr) technique in slab continuous casting[J]. Metall. Res. Technol., 2021,118(2):218-234. doi: 10.1051/metal/2021016 [15] XU L, WANG E, KARCHER C, et al. Numerical simulation of the effects of horizontal and vertical EMBr on jet flow and mold level fluctuation in continuous casting[J]. Metall. Mater. Trans. B, 2018,49(5):2779-2793. doi: 10.1007/s11663-018-1342-4 [16] LI Z, WANG E, ZHANG L, et al. Influence of vertical electromagnetic brake on the steel slag interface behavior in a slab mold[J]. Metall. Mater. Trans. B, 2017,48(4):2389-2402. [17] XU L, KARCHER C, WANG E. Numerical simulation of melt flow, heat transfer and solidification in CSP continuous casting mold with vertical-combined electromagnetic braking[J]. Metall. Mater. Trans. B, 2023,54(4):1646-1664. doi: 10.1007/s11663-023-02784-7 [18] XU L, HAN Z, KARCHER C, et al. Melt flow, heat transfer and solidification in a flexible thin slab continuous casting mold with vertical-combined electromagnetic braking[J]. J. Iron Steel Res. Int., 2024,31(2):401-415. doi: 10.1007/s42243-023-01062-9 -
下载:
点击查看大图
计量
- 文章访问数: 46
- HTML全文浏览量: 19
- PDF下载量: 4
- 被引次数: 0
