0.   引言

钛是20世纪50年代发展起来的一种轻质结构金属，从飞机零部件、汽车结构框架到人体的某些器官、假肢、牙齿等都有钛及钛合金的存在，它在高端技术和前沿科学上起着重要作用，己经成为新的工艺及设备不能缺少的金属材料 ^[1]。钛合金在经过锻造、挤压、轧制和拉拔等一系列加工工序后能得到管材、板材、型材和棒材等产品，但在加工过程中会由于应力不均匀、堆放等多种原因出现弯曲，要满足后续加工工程结构件对平直度的要求就要对其进行矫直处理。

热张力矫直是在待矫直钛合金两端通以电流，靠自身的电阻使电能转化为热能加热并对其施加拉力，实现形状矫直。目前已有学者利用有限元模拟对金属材料的热变形过程进行分析，KIM等人^[2]对小直径的钨线和钢管进行在线加热拉伸矫直，研究了保护气体的流速、矫直电流及矫直力等工艺参数对矫直材料平直度的影响。王小红等人^[3]运用MARC有限元软件对AZ31镁合金棒材拉伸矫直变形过程进行数值仿真计算，并就棒材原始弯曲度、直径、矫直温度、拉伸位移对直线度的影响进行了研究，得到矫直工艺参数、残余弯曲度和材料几何尺寸的关系数学模型。ZHANG等^[4]利用有限元模拟分析了大型铝合金板材淬火后的预拉伸过程，发现拉伸应变在1%到3%时铝合金的残余应力大幅降低，且板形改善较为明显。杜红娥、贾春莉等^[5]利用有限元软件对 TC4 管件接头热成形的过程进行数值模拟，分析了工艺参数对成形性能的影响，实现了温度参数的优化。

目前对热张力矫直的有限元分析研究主要集中在铝合金和镁合金上，对钛合金热张力矫直工艺的报道较少，并且钛合金热张力矫直工艺受到多个参数的影响，为提高矫直直线度以满足产品精度要求，迫切需要探寻最佳矫直工艺参数。目前市面上的大多数矫直设备只是依据一线工作人员的经验进行矫直操作，缺少系统而精确的工艺参数，也缺乏相应的理论支撑。因此，笔者以TC4棒材为研究对象，结合有限元软件进行数值模拟，分析钛合金棒材在电矫直过程中的应力应变分布，同时预测矫直后的回弹现象。此外，通过改变矫直温度、保温时间和拉伸量等工艺参数，分析不同工艺参数对矫直效果的影响，并揭示出影响的机理。最后，通过矫直物理试验对有限元模型的有效性进行验证。

1.   材料与方法

1.1   试验材料

以直径为10 mm，长度1000 mm的退火态TC4合金棒材为研究对象。棒材的化学成分见表1^[6]。

表  1  TC4钛合金的化学成分

Table  1.  Chemical compositions of TC4 titanium alloy %

Ti	V	Al	Fe	C	N	H	O	其他
基体	4.5	6.8	0.30	0.10	0.05	0.015	0.20	0.02

下载: 导出CSV 

| 显示表格

1.2   材料模型

1.2.1   TC4的拉伸性能

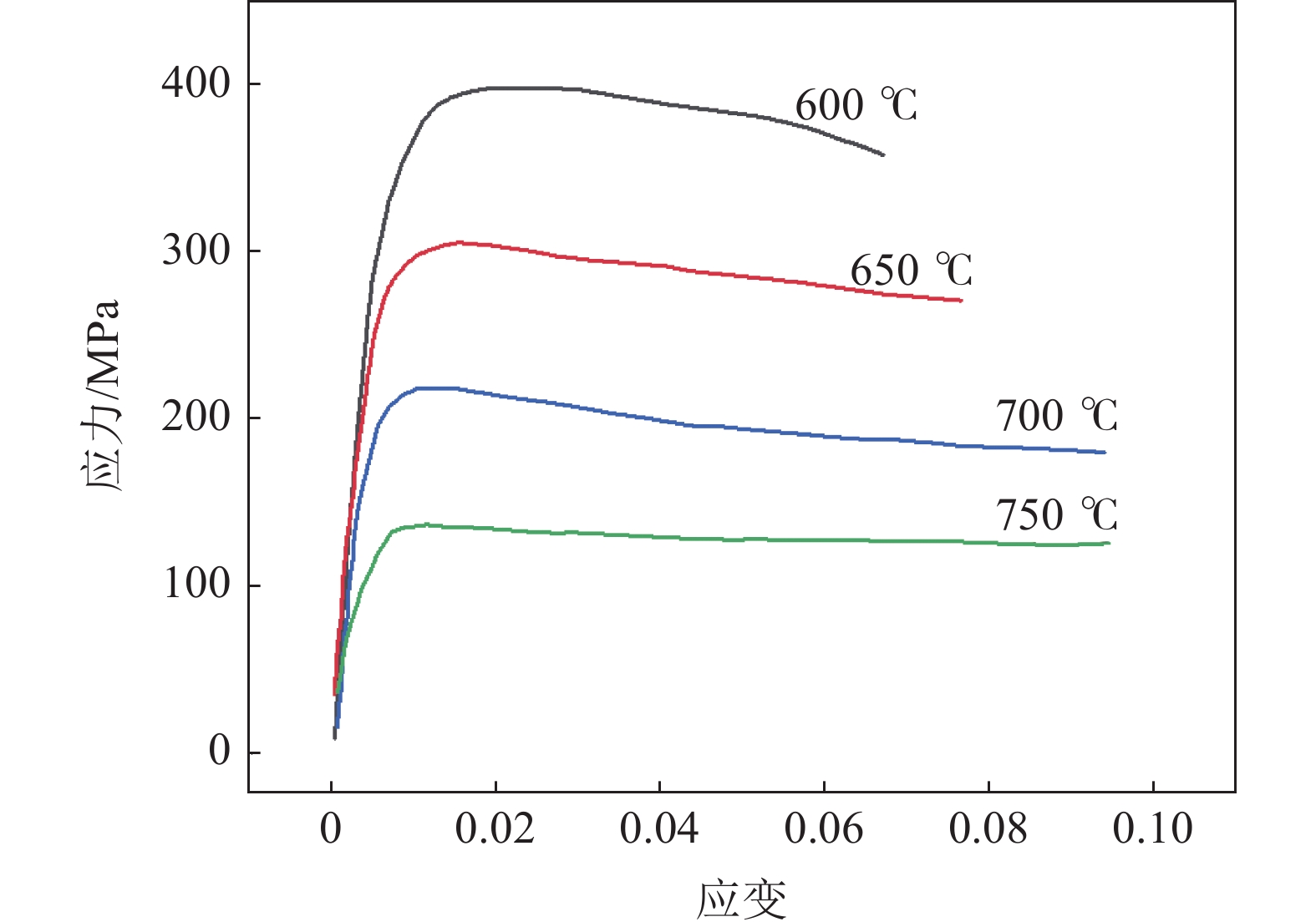
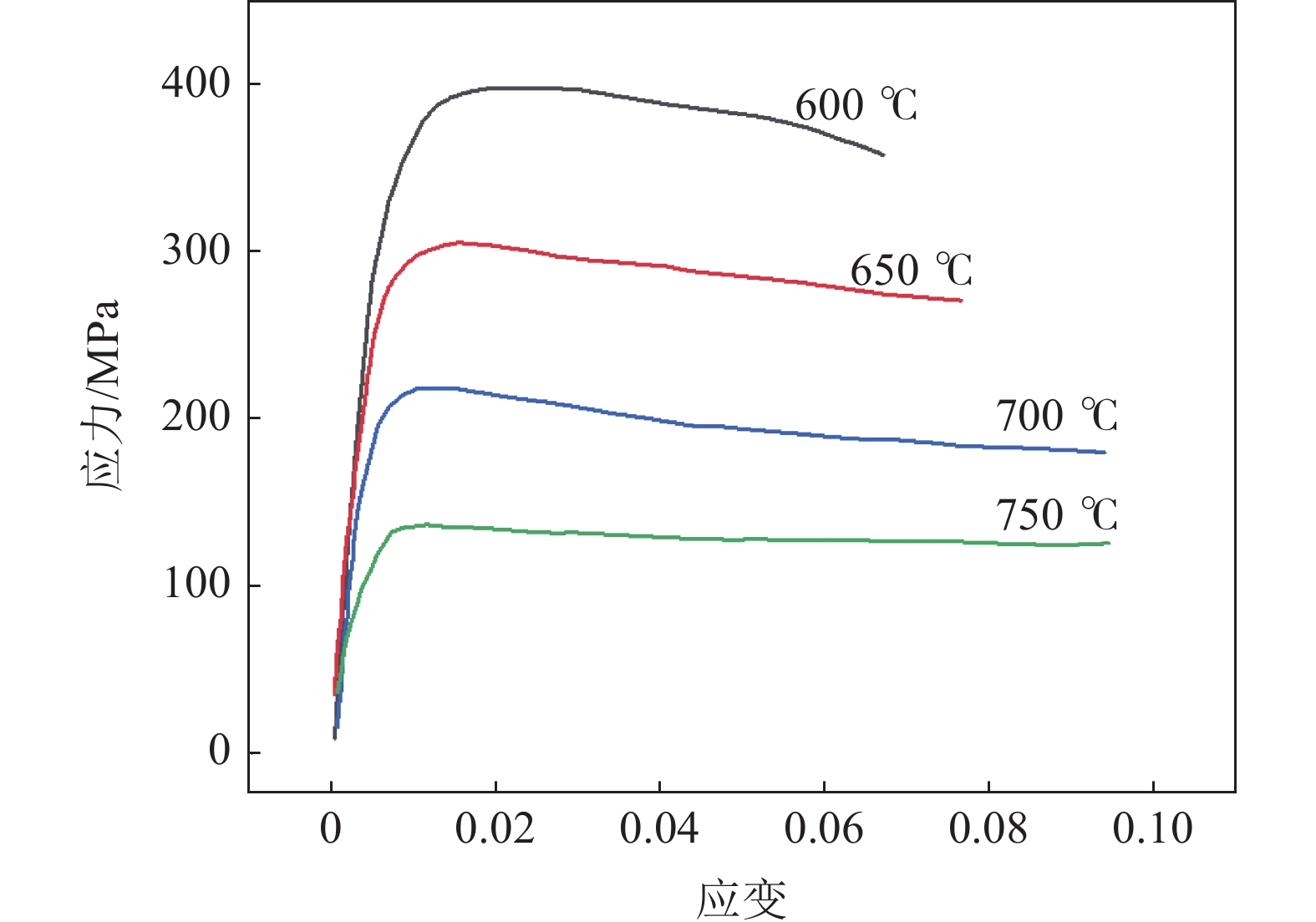
图1为TC4钛合金在1×10⁻⁴/s应变速率下不同拉伸温度的流变应力曲线^[7]。在应变速率一定时，TC4钛合金在高温条件下的拉伸强度明显小于室温拉伸时的强度，拉伸时应力快速到达峰值后会有所下降。流变应力主要受硬化和软化行为的影响，而硬化和软化行为取决于温度和应变速率^[8−10]，本次主要考虑温度对其影响。材料开始变形时，加工硬化使材料的流变应力迅速增大，达到峰值后，应力随应变的增加而逐渐减小。在相同的应变速率下，应力随着温度的升高而减小，这是因为金属内部原子的热运动随温度的升高而加剧，而且高温使得动态回复和再结晶更容易进行，降低金属内部的位错密度，进而减弱加工硬化现象，减小流动应力。TC4棒材的拉伸性能可以在ABAQUS软件中用多段法导入。

图  1  TC4在不同拉伸温度下的应力-应变曲线^[7]

Figure  1.  Stress-strain curves of TC4 at different tensile temperatures^[7]

下载: 全尺寸图片 幻灯片

1.2.2   TC4的应力松弛

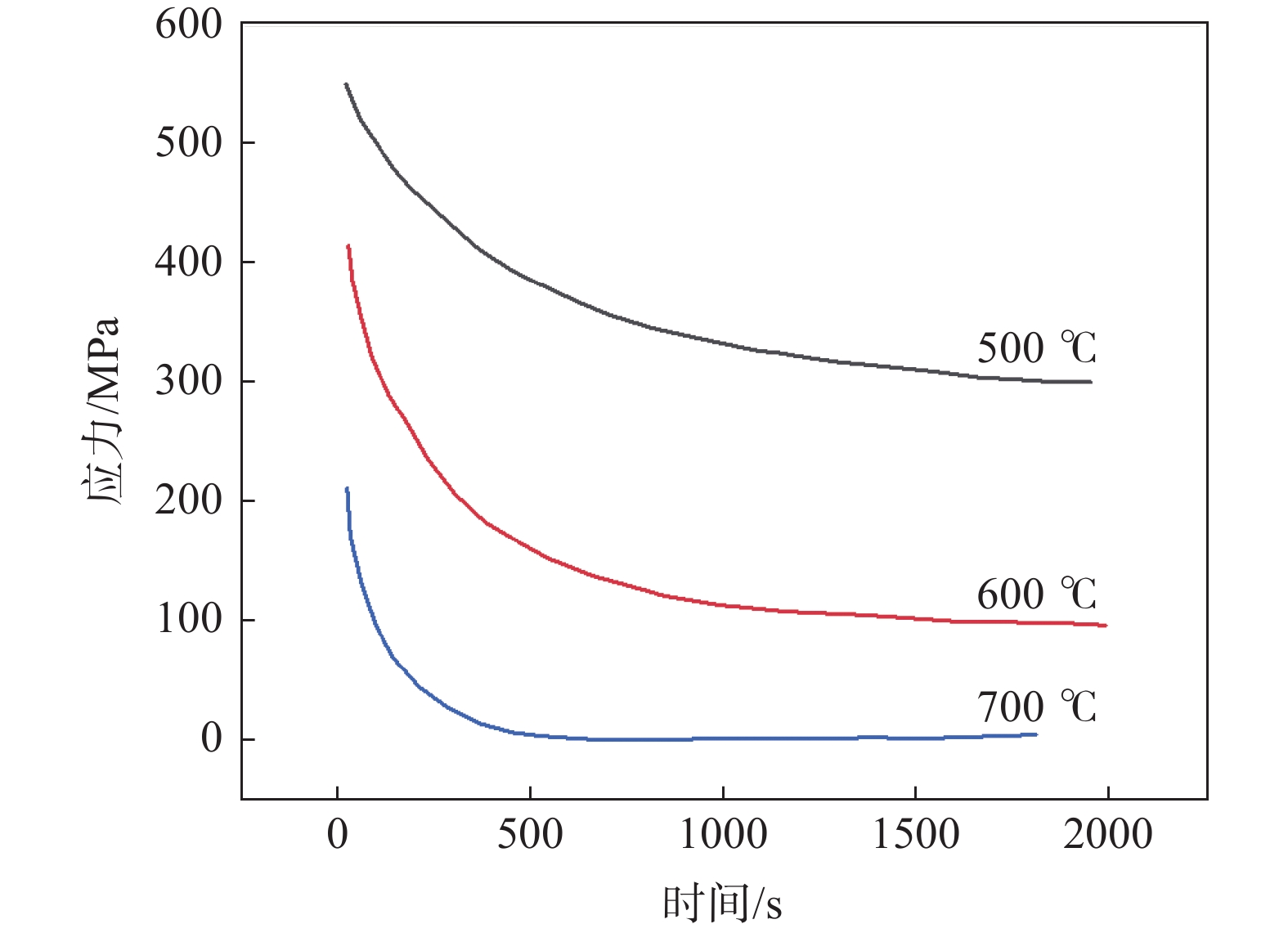
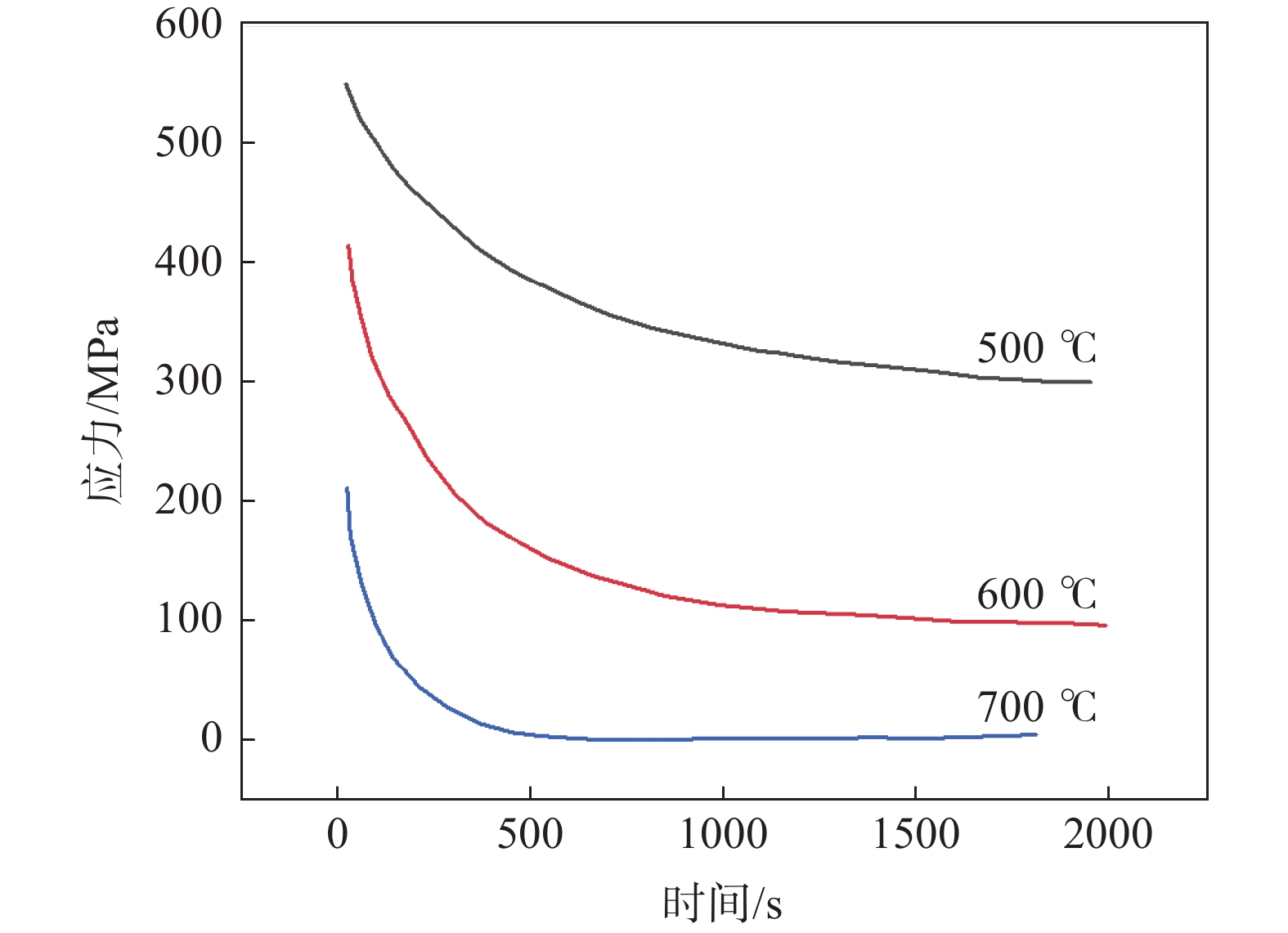
应力松弛是金属材料在保持总应变不变的情况下，内部应力随着时间的增加而减小的现象。TC4钛合金在不同温度下的应力松弛曲线有着相似的变化趋势(图2)^[7]：第一阶段应力快速下降；第二阶段松弛过程明显放缓，应力下降速率十分缓慢，并最终接近于某一定值，此定值称为应力松弛极限。温度越高，TC4钛合金第一阶段的应力松弛速率越大，应力松弛极限也越小。

图  2  TC4在不同拉伸温度下的应力松弛曲线^[7]

Figure  2.  Stress relaxation curves of TC4 at different temperatures^[7]

下载: 全尺寸图片 幻灯片

1.2.3   TC4蠕变本构模型

应力松弛曲线不能直接输入到有限元软件，需要根据应力松弛结果数据计算本构模型后再导入。应力松弛和蠕变具有内在的统一性。因此，可以利用蠕变模型来描述应力松弛效应。研究采用Zener-Hollomon参数和Arrhenius本构模型来定义TC4棒材的蠕变行为。模型计算公式为式(1)～(3)^[11−13]。

其中A, n₁, n，α，β是材料常数，$ \dot{{\varepsilon }_{c}} $为蠕变应变率(s⁻¹)；R为通用气体常数(8.314 J·K/mol)； Q为热变形活化能(J/mol)；T为温度(K)；σ为流动应力(MPa)；具体的计算过程及参数见参考文献[7]。

2.   数值模拟试验方法及结果

2.1   几何模型

TC4棒材矫直几何模型如图3所示，棒材的形状被设定为均匀的弯曲变形，直径为10 mm，外形长度1000 mm，弯曲挠度43.5 mm。

图  3  棒材初始形状的几何模型

Figure  3.  Geometric model of the initial shape of the bar

下载: 全尺寸图片 幻灯片

在建立有限元模型时，为了简化矫直过程变形及残余应力场的计算，采用了如下假设：忽略夹持端；TC4棒材为各向同性弹塑性材料，各处温度均匀，无温度梯度；矫直前弯曲棒材内无应力，拉伸时水平方向匀速运动。

2.2   热-力耦合模型

在ABAQUS软件中建立了TC4钛合金棒材热张力矫直过程的数值模拟模型，分为以下步骤：拉直、加热、热拉伸、保温、降温和卸载反弹。配置文件为8节点简化集成热耦合元件(C3D8T)。截面上的单元尺寸范围为1～2 mm。棒材长度方向上的单元尺寸为10 mm。网格模型如图4所示。在保温步骤中采用粘式分析步，其余步骤使用温度-位移耦合（瞬态）分析步，每一步的初始变形和应力场依次继承于前一步的结果文件^[14−16]。

图  4  待矫直棒材的网格模型

Figure  4.  Meshed model of the bar to be straightened

下载: 全尺寸图片 幻灯片

2.3   回弹设置

将棒材拉直卸载后会有一定的弹性回复量，从而导致金属棒材的直线度降低，因此必须考虑到拉伸卸载后发生的弹性变形，即回弹。基于上一节中建立的矫直过程仿真模型，卸载回弹步骤中采用了重启动分析，将冷却至室温后的模型odb文件导入回弹预测模型中，通过预定义场赋予回弹件初始应力状态。为消除刚体位移，把棒材中心位置固定。建立的回弹预测模型如图5所示。

图  5  回弹预测模型

Figure  5.  Springback prediction model

下载: 全尺寸图片 幻灯片

2.4   试验方案

在矫直过程中，影响棒材平直度的参数有很多，如矫直温度、初始弯曲挠度、保温时间及伸长量等。根据实际情况，利用数值模拟探讨温度、保温时间和伸长量对矫直的影响。根据实际矫直工艺状态，通过控制变量法设计模拟试验，试验方案如表2所示。以矫直后的直线度和残余应力为指标，并结合实际工况进行工艺优化。

表  2  模拟试验方案

Table  2.  Simulation experiment scheme

试验方案	温度/℃	保温时间/s	伸长量/%
1	600	30	2
2	650	30	2
3	700	30	2
4	750	30	2
5	800	30	2
6	700	1	2
7	700	10	2
8	700	60	2
9	700	120	2
10	700	30	1
11	700	30	3

下载: 导出CSV 

| 显示表格

为表征棒材直线度，沿棒材轴向取一条路径，从棒材一端到另一端提取节点位置坐标值(X、Y坐标)，相邻节点间间距范围为10~100 mm。建立棒材直线度α表达式，如式(4)所示。

其中，h₁表示路径弯曲图的最高点纵坐标； h₂表示路径弯曲图的最低点纵坐标； l₁表示拉伸后试样原 1 000 mm 标记段在水平面上的投影长度，拉矫后直线度α数值越小，矫直效果越好。

2.5   验证试验方法

为验证数值模拟模型的准确性，使用和数值模拟部分直径、长度和挠度一样的TC4棒材进行电张力矫直试验。具体试验步骤为：①将棒材装上矫直机，并在室温下把弯曲棒材拉直；②在电加热的辅助下，将棒材加热到目标温度；当达到设定温度后，通过拉伸对棒材进行矫直，拉伸量为2%；③为降低内应力，将棒材进行保温处理；④冷却至室温并卸载。把棒材放置在水平操作台上用塞尺统计拉伸后的棒材挠度，并根据式（4）计算出直线度。

3.   模拟结果

3.1   棒材矫直过程中的应力场

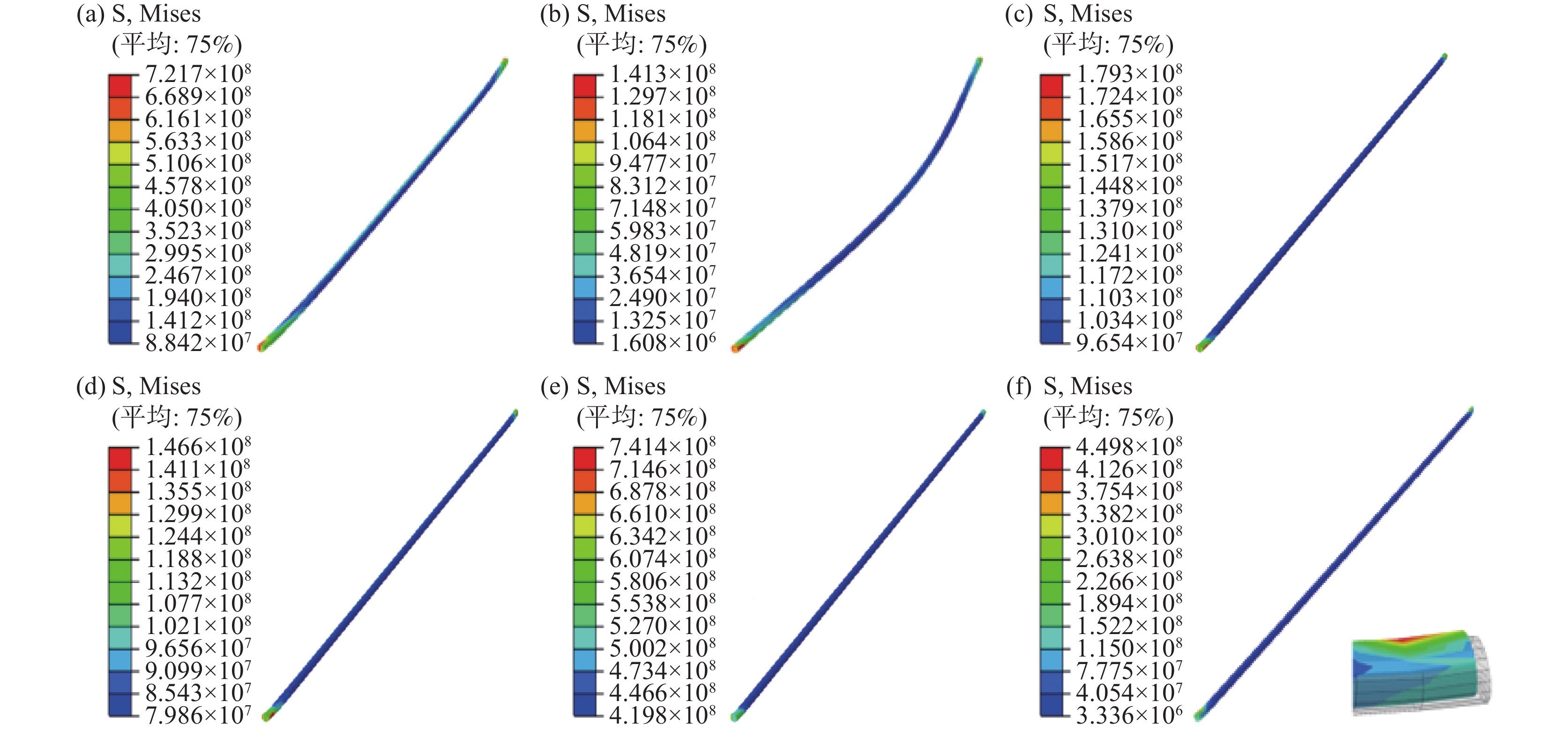
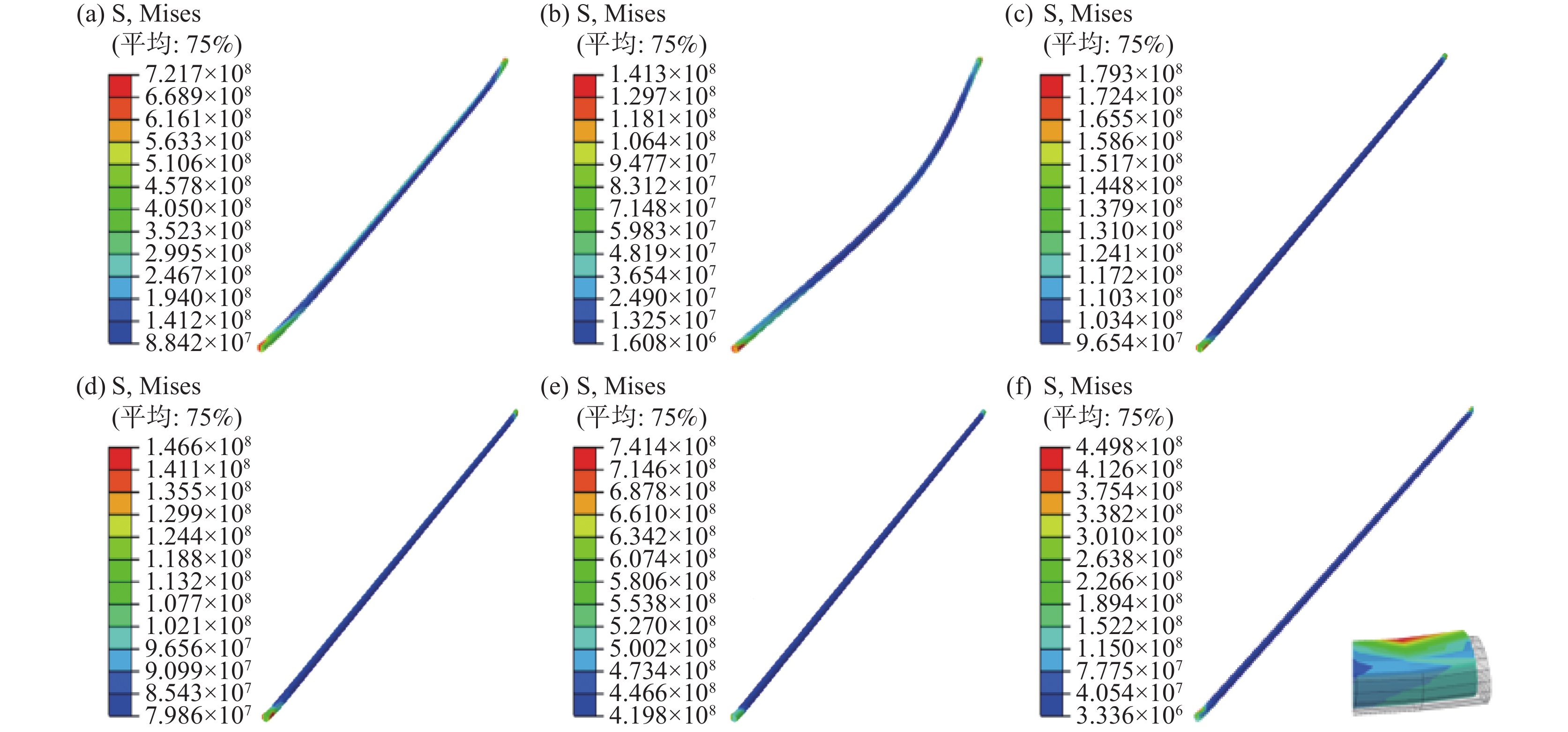
不同矫直步骤后的棒材应力分布如图6所示。把弯曲的棒材拉直后形状有所改善，但此时棒材内部存在较大的应力，尤其两端被束缚会影响变形区域的金属流动和变形，产生较大的应力，并且棒材中间部分弯曲变形量较大，因而中间位置的应力也相应较大，见图6(a)；棒材被加热到目标温度后因软化和重力作用中间下落，此时棒材整体应力随温度的升高而下降，见图6(b)；在热拉伸阶段，把软化变弯的棒材拉直，此时应力随应变的增加而提高，见图6(c)；由于应力松弛效应，在保温过程中随着保温时间的增加，棒材应力明显降低，见图6(d)；将棒材冷却至室温，随着温度的降低应力有所回升，见图6(e)；卸载后应力释放产生与弯曲方向相反的弯矩，从而产生一定程度的弹性回弹，见图6(f)。

图  6  矫直过程仿真

(a)拉直；(b)加热；(c)热拉伸；(d)保温；(e)冷却；(f)反弹

Figure  6.  Simulation diagrams of the straightening procedure

下载: 全尺寸图片 幻灯片

3.2   矫直工艺参数对TC4棒材矫直效果影响

在研究矫直过程中各工艺参数(温度、保温时间和热拉伸伸长量)对棒材直线度影响的同时，还要考虑其对残余应力的影响，如果矫直后的棒材内部残余应力过大，在后续加工中会引起潜在的形状不良，故以直线度和残余应力为指标来判断TC4棒材矫直后的效果，进而得出可以提升棒材综合矫直质量的工艺参数。

3.2.1   温度对矫直效果的影响

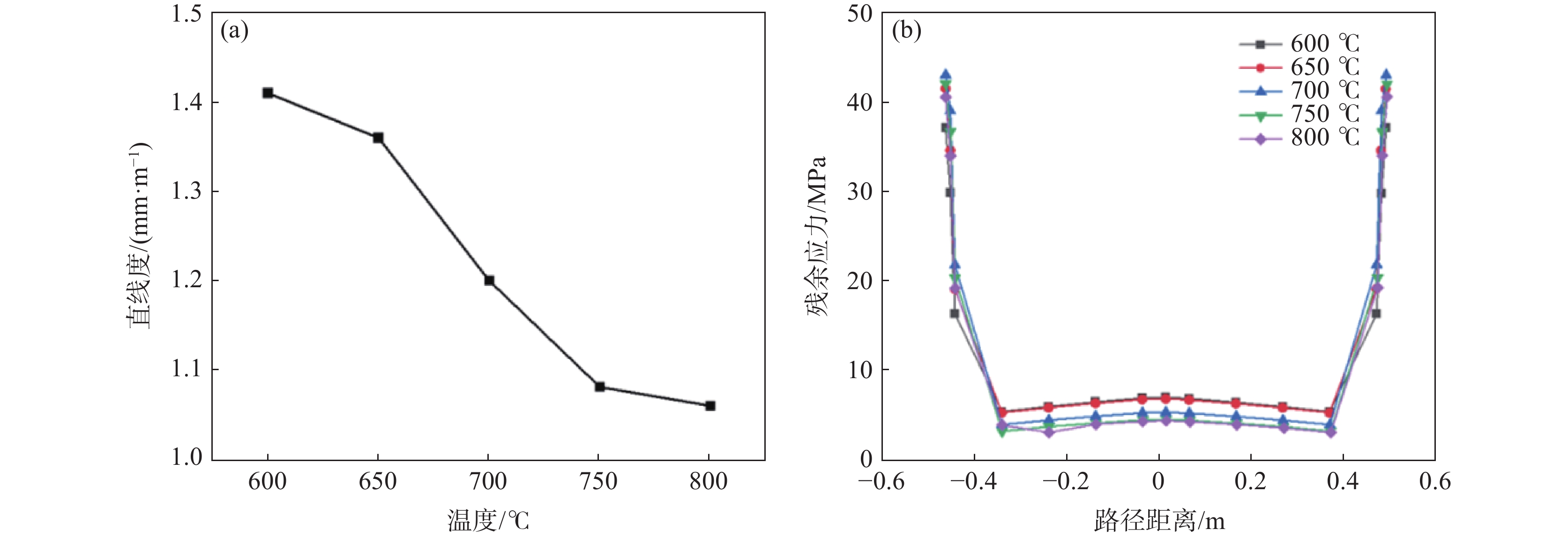
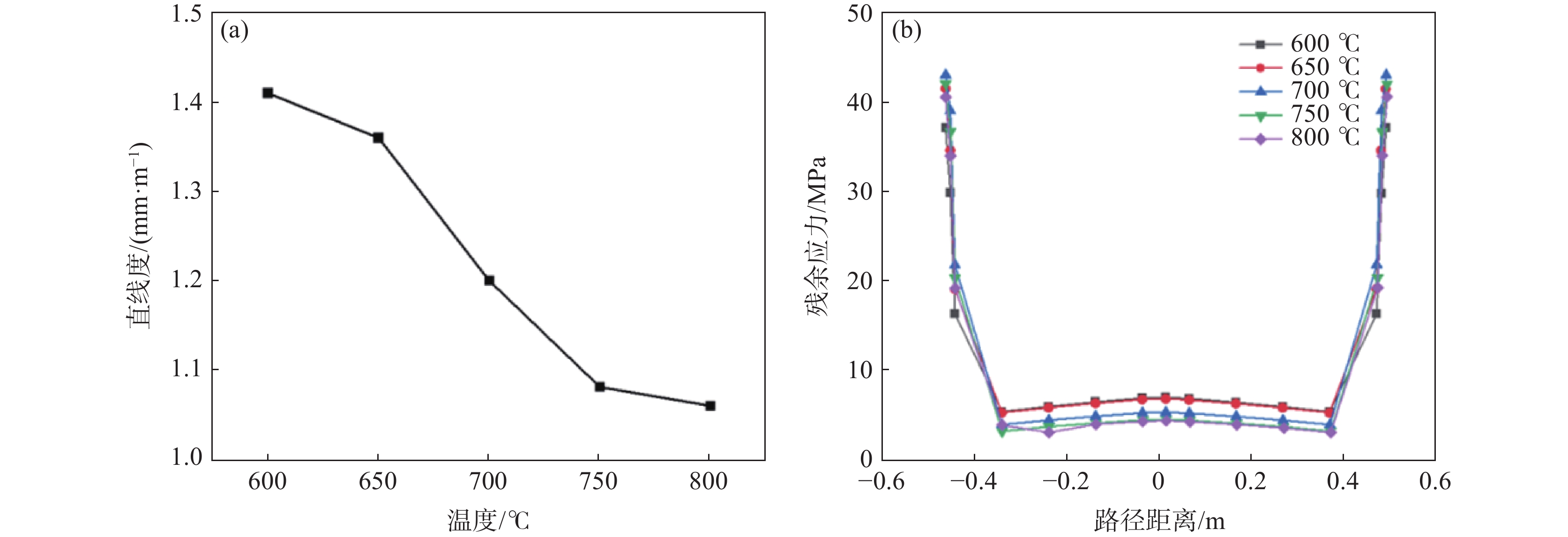
TC4 钛合金材料在不同温度下的力学性能存在差异，随着温度的升高表现出良好的塑性，因此在电张力矫直过程中，温度是影响矫直效果的重要工艺参数之一。利用上述模型模拟了棒材保温时间为30 s、伸长量为2%时不同温度下(600、650、700、750、800 ℃)矫直的效果（表2中的试验1～5）。

由图7可知，棒材的直线度随矫直温度的升高而降低，当温度从650 ℃增加到800 ℃时，直线度由1.41 mm/m降低到1.06 mm/m，残余应力从7.15 MPa减小到4.55 MPa，如图7(b)所示，相对减小幅度达36.4%，并且棒材两端应力明显高于其他位置，在实际生产中会根据实际情况把两端夹持区域切掉。金属材料在一定温度环境下产生变形之后，保持总应变量不变，其内部应力会随着时间的增加而降低，即应力松弛现象，也就是材料总的宏观变形量保持不变，而部分弹性应变向塑性应变转化的过程。矫直温度影响棒材的应力值，由前述可知，矫直温度越高，应力松弛效果越明显。应力松弛的本质是位错和亚晶界的运动以及原子扩散。温度越高，金属材料内部的原子活动越剧烈，越有利于进行原子扩散和位错的滑移与攀移，应力松弛过程进行得越快，在一定时间里应力下降得也就越多。卸载前应力水平越小，卸载后的回弹值越也就越小。因此，随着矫直温度的升高，TC4钛合金棒材矫直后的残余应力减小，直线度也逐渐改善。

图  7  不同温度下矫直效果

(a)直线度；(b)轴向残余应力分布

Figure  7.  Straightening effect at different temperatures

下载: 全尺寸图片 幻灯片

3.2.2   保温时间对矫直效果的影响

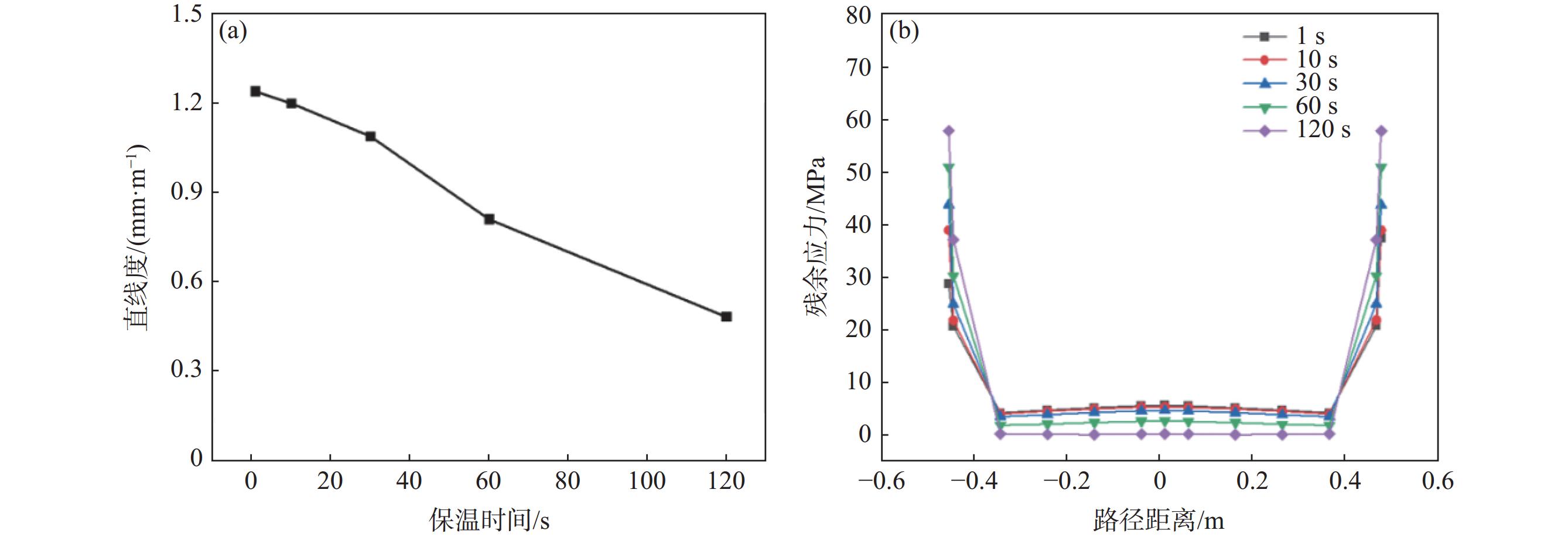
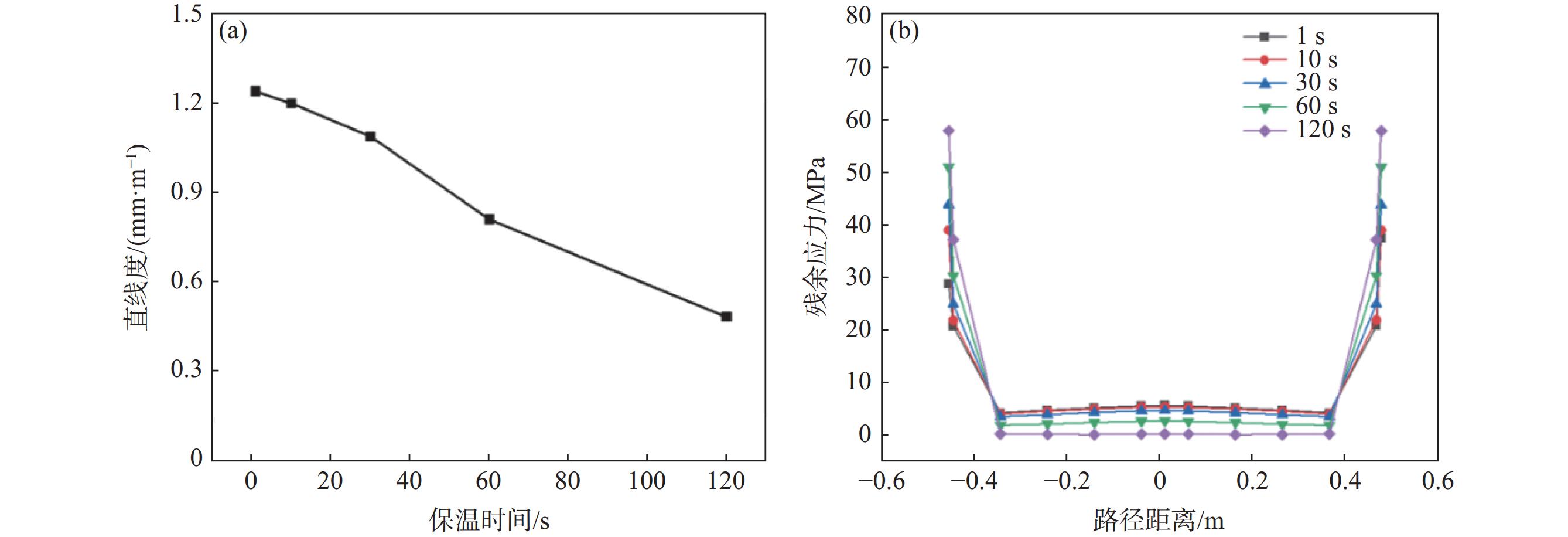
为探究钛合金电张力矫直过程中不同的保温时间对TC4棒材矫直效果的影响，进行了700 ℃和热拉伸伸长量2%条件下分别保温1、10、30、60、120 s的模拟试验（表2试验6～10）。

可以看出，保温时间越长，棒材矫直后的直线度越低，残余应力亦明显降低，如图8(a)(b)所示。当保温时间从1 s增加到120 s时，平均残余应力从5.75 MPa减小到0.3 MPa，相对减小幅度达94.78%。保温时间对直线度和残余应力的影响机理及温度的影响机理一致，本质上都是由温度引起的，温度一定时，随着保温时间的增加，应力松弛量越多，弹塑性应变转化也就越彻底，故棒材的残余应力就越小，棒材直线度也越小。

图  8  不同保温时间下矫直效果

(a)直线度；(b)轴向残余应力

Figure  8.  Straightening effect at different holding time

下载: 全尺寸图片 幻灯片

3.2.3   拉伸量对矫直效果的影响

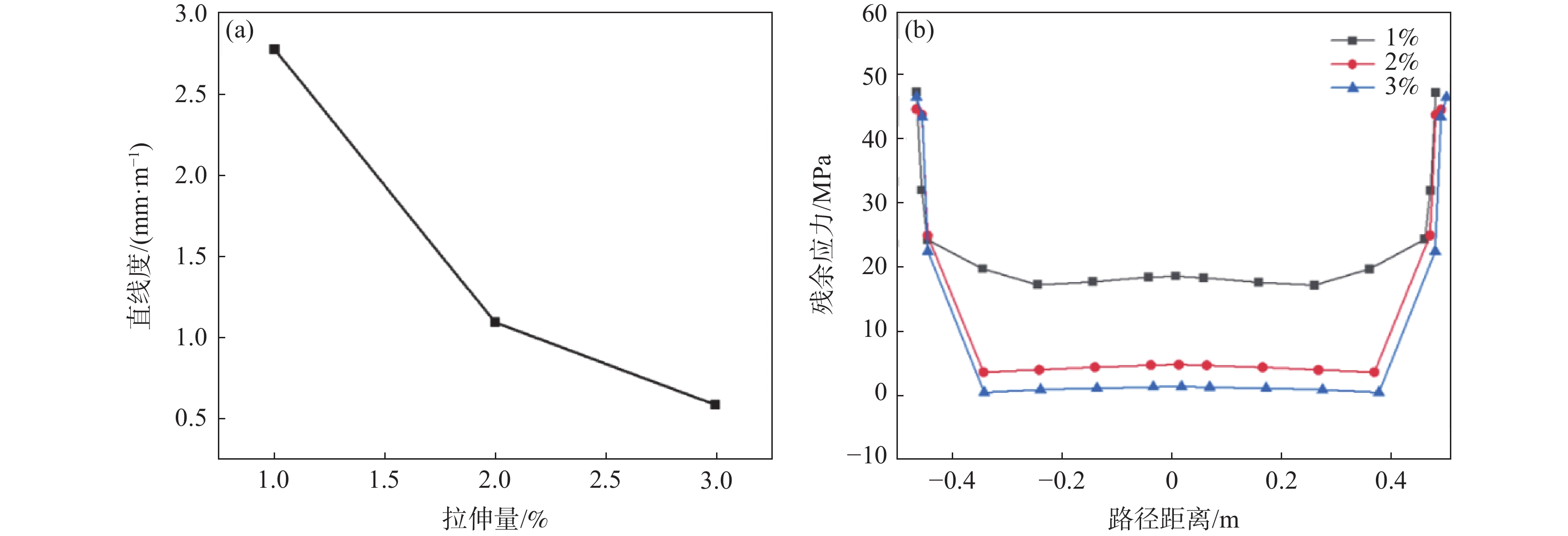
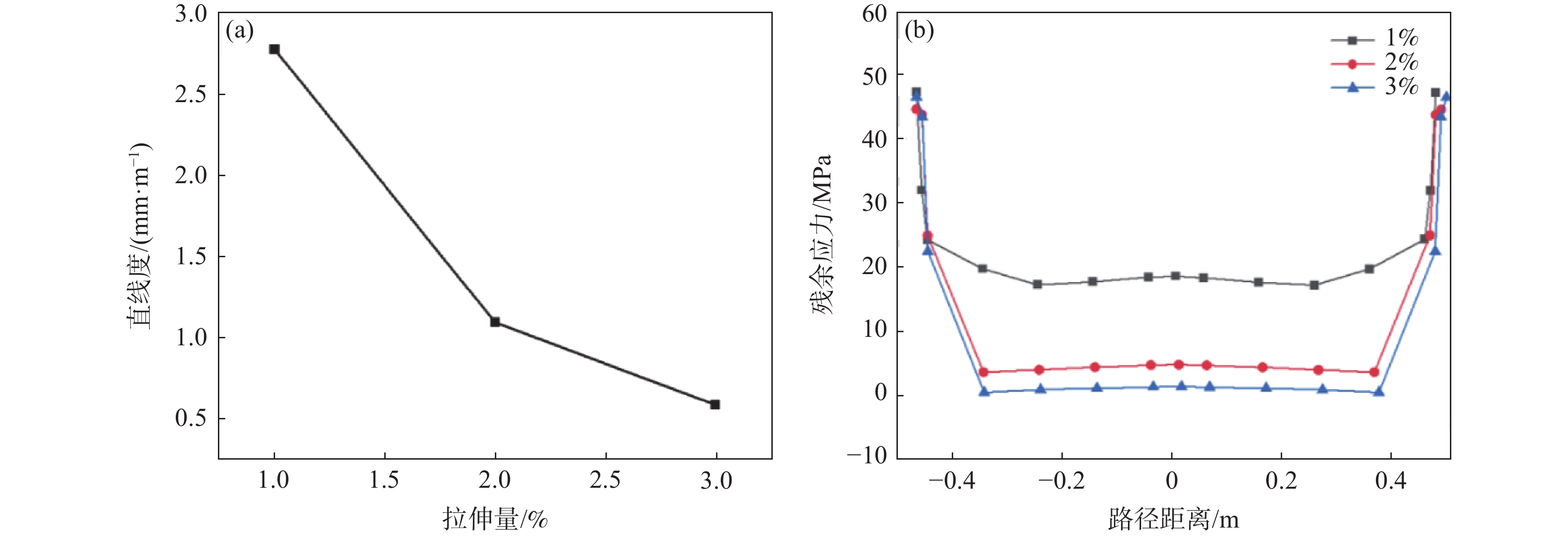
拉伸量是拉伸矫直工艺中一个非常重要的参数，拉伸量过小会导致材料塑性变形不充分，棒材的残余应力和弯曲度不能得到很好的消除；拉伸量过大时，棒材表面会产生滑移线进而造成新的应力不均，甚至造成棒材的断裂。所以，制定合理的热拉伸量对于钛合金棒材的矫直效果有重要意义。为探寻合适的拉伸量，进行了700 ℃保温30 s条件下，拉伸伸长量为1%、2%、3%的模拟试验（表2中的试验3及试验10～11），模拟结果如图9所示。

图  9  不同伸长量下矫直效果

(a) 直线度；(b)轴向残余应力

Figure  9.  Straightening effect at different elongation

下载: 全尺寸图片 幻灯片

当伸长量是棒材总长的1%时，棒材矫直后的直线度减小到2.7 mm/m，拉伸量增加到3%时，棒材的直线度进一步减小，但减小的幅度越来越小(图9(a)) ，由60.8%降低到46.8%。拉伸量在2%时，其直线度就已达到国家对棒材直线度的标准要求(不超过2 mm/m)。图9(b)为棒材轴向残余应力的分布情况，可以看出，拉伸量的增大不仅可以改善棒材的直线度，也能减小棒材的残余应力，当拉伸量在1%到3%时，残余应力依次由18.6 MPa降到1.31 MPa。原因是对于先拉直再加热的钛合金棒材，在经过拉直步骤后应力大幅上升，最高达358 MPa，经加热软化后应力有所下降，但仍存在25.4 MPa的残余应力。在热拉伸阶段给予1%～3%的变形量，实质上就是把棒材内部的残余应力进行重新分布，不管是受拉应力的弯曲外侧金属，还是受压应力的弯曲内侧金属(如图10所示)，再次受到外力作用时均会发生变形，当施加的拉伸量超过金属的弹性变形极限后就产生塑性变形。因为棒材的弯曲外侧金属经拉直和加热步骤后具有残余拉应力，所以它比内侧弯曲金属较快进入塑性变形，也就导致了弯曲外侧金属比弯曲内侧金属变形速度快，但是由于金属棒材作为一个整体, 弯曲内侧金属将牵制外侧金属的变形，所以在热拉伸产生塑性变形以后，弯曲内侧金属将产生拉应力，而弯曲外侧金属产生压应力，这正好和热拉伸前棒材弯曲内外侧的残余应力方向相反，此时棒材中的残余应力就是热拉伸前棒材中的残余应力和热拉伸时产生的内应力之差，若拉伸量选择合适，它们的差能够接近零。虽然随着拉伸量的增大应力差在一直减小，但是拉伸量从1%到2%时应力差较大，当伸长量增大到3%时应力差降低的幅度有所减小，拉伸量增大的过程中，应力中性面逐渐向心部靠近，应力变化量减小。

图  10  热拉伸前棒材弯曲内外侧受力示意

Figure  10.  Schematic diagram of the force on the inside and outside of the bar bending before hot drawing

下载: 全尺寸图片 幻灯片

随着拉伸量的增大，材料表面会出现滑移线，棒材极易发生断裂，由此拉伸量也并非越大越好，2%的拉伸量就能够满足工业标准要求。并且在实际生产中，热张力矫直过程是在空气中进行，钛合金在高温环境下极易氧化，温度太高和保温时间过长会造成TC4钛合金的晶粒长大和组织变化，并且加剧氧化反应和吸氢反应，影响棒材的力学性能。故从综合矫直效果考虑，该钛合金棒材的最佳矫直温度为750 ℃、保温时间为10 s、伸长量为2%。

4.   物理试验验证

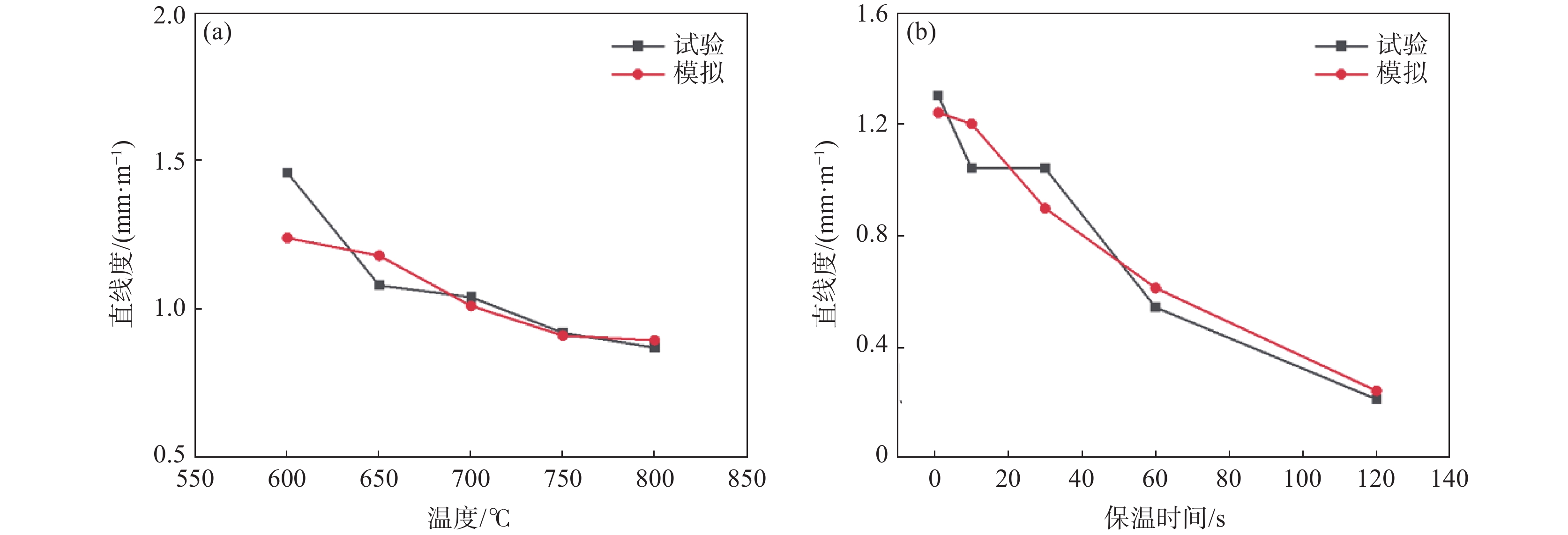
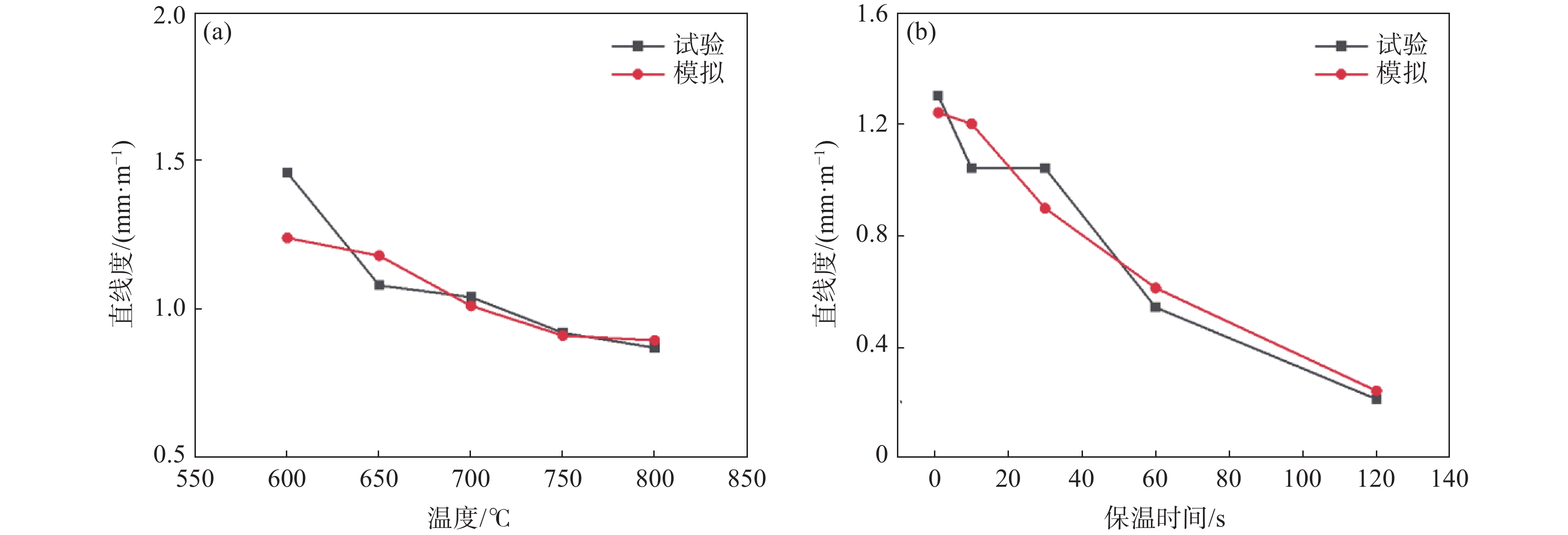
矫直拉伸量为2%、保温时间为30 s时，不同矫直温度下棒材直线度的测量结果与模拟结果的对比如图11(a)所示。随矫直温度的增加，棒材矫直后的直线度逐渐减小，与模拟试验结果规律一致，试验和模拟结果比较，其直线度的最大差异为19.5%。矫直拉伸量为2%、温度700 ℃时，不同保温时间下残余挠度的测量结果与模拟结果的比较如图11(b)所示，随保温时间的增加，矫直后棒材的直线度逐渐减小，与模拟试验结果规律一致，试验和模拟结果比较，其直线度的最大差异为15.38%。由图11的对比分析可知，该预测模型与实际试验结果相对误差不到20%，能够较好地揭示出矫直工艺参数对TC4棒材矫直的影响规律。

图  11  模拟与试验结果对比

(a)温度；(b)保温时间

Figure  11.  Comparison of simulation and experimental results

下载: 全尺寸图片 幻灯片

5.   结论

1)建立了TC4钛合金棒材电张力矫直弹塑性变形过程的有限元仿真模型，采用重启动方法预测棒材矫直后的直线度，该模型揭示的样本空间内矫直工艺参数对直线度的影响规律与试验结果较为一致。

2) 利用控制变量法对矫直工艺参数进行分析，结果显示，随着保温时间、矫直温度和热拉伸量的增加，棒材的直线度和残余应力减小。结合实际生产工况，750 ℃的矫直温度，2%的热拉伸量和10 s的保温时间为该钛合金棒材矫直的最佳工艺参数。

3) 进行了钛合金电张力矫直物理试验，模拟与试验结果具有相同的变化趋势，两者误差小于20%，验证了所建立的数值模拟模型的准确性。