Research on the characteristics of cold-rolled deformation zone of thin strip and the applicability of contact pressure model
-
摘要: 薄带冷轧过程中轧辊会产生不同程度的弹性压扁现象，而各变形区理论对该现象认识的不同导致其计算精度和适用范围存在显著差异。为此采用有限元手段分析了薄带冷轧过程中变形区特征的变化规律，并对比探究了Stone全滑移、Johnson全弹性和组合型三种接触压力模型的推导特点、成立的先决条件和适用区间。结果表明：变形区轮廓随轧辊弹性压扁程度的加剧依次经历了圆弧形、圆弧压扁增大形、非圆弧形和近直线形，中性区的出现及其所占变形区比例的不断增加是导致实际压下率快减和变形区形状系数快增的主要原因。通过对比变形区接触压力曲线的模拟值与理论值可发现，Stone模型、Johnson模型和组合型模型分别适用于道次压下率大于10%、小于1%和1%～10%的轧制工况。Abstract: In the process of cold rolling of thin strip, the roll will produce different degrees of elastic flattening, and the different understandings of this phenomenon in each deformation in each deformation zone theory lead to significant difference in its calculation accuracy and application range. Therefore, the finite element method is used to analyze the variation law of the characteristics of the deformation zone in the process of cold rolling of thin strip, and the derivation characteristics, prerequisites and applicable intervals of the three contact pressure models of Stone total slip, Johnson full elasticity and combined type are compared and explored. The results show that with the increasing of the elastic flattening degree of the roll, the contour of the deformation zone undergoes arc shape, arc flattening enlargement, non-arc shape and nearly linear shape, and the occurrence of neutral zone and the increasing proportion of the deformation zone are the main reasons for the rapid decrease of the actual depression rate and the rapid increase of the shape coefficient of the deformation zone. By comparing the simulated and theoretical values of the contact pressure curve in the deformation zone, it can be found out that the Stone model, Johnson model and combined model are suitable for rolling conditions where the pass reduction ratio is greater than 10%, less than 1% and 1%～10%, respectively.
-
0. 引言
微电子、新能源和高端化工等领域的快速发展导致对高品质技术密集型金属薄带材的需求大幅提升，同时也促进了薄带轧制变形区理论的不断发展与完善[1-2]。薄带冷轧过程中接触界面复杂的应力状态极易导致轧辊发生弹性压扁，然而由于对上述现象认识和处理方式的不同导致各变形区理论模型成立的先决条件和适用范围存在显著差异[3-4]，故理解并选择合适的理论模型对提高变形区接触特征的预测精度和避免不必要的工艺浪费是至关重要的。
薄带轧制变形区理论是伴随着对变形区接触轮廓、界面摩擦条件和轧件弹塑性状态转变等认识的不断深入而发展的。Karman等[5]将薄带轧制视为平面应变问题，忽略了轧辊弹性变形，并基于平衡方程、Tresca屈服方程和库伦摩擦条件等推导出了单位压力微分方程。Kuhn等[6−7]发现宽薄带轧制时辊缘接触会吸收部分辊力，但并不会严重限制辊带的可用载荷率，且边缘处侧向压力对整体屈服行为的影响基本可以忽略不计。Hitchcock等[8]假设弹性压扁后的轧辊轮廓为半径增大的圆弧，随后Stone等[9]则采用Hitchcock弧长公式推导了单位压力方程和最小可轧厚度。然而，大量研究发现轧辊弹性压扁后并非始终保持圆弧形轮廓，也并非始终满足库伦摩擦条件的假设[10−12]。Orowan等[13]根据Prandtl和Nadai的二维无限长平板压缩研究建立的单位压力方程，考虑了轧辊弹性变形并指出轧辊与轧件接触界面存在滑移和黏着两种现象。Ford等[14−15]在全弹性带基础上提出变形首先发生于中心截面处，但该假设并不符合实际。Bentall和Johnson等[16−17]则基于赫兹弹性理论提出变形区存在无相对滑移的零压下区，随后Fleck等[18−19]提出轧辊弹性压扁后呈非圆弧形轮廓，并在前者基础上修正了赫兹接触模型，将整个变形区划分为若干分区。Liu和Xiao等[20−22]则在非圆弧轮廓的基础上赋予Stone模型新的含义，并提出了新的适轧厚度和最小可轧厚度理论公式。李伟等[23]则在赫兹理论基础上提出了基于轧制力判定的薄带材极限可轧厚度理论公式，除此之外，还考虑了薄带力学行为各向异性对变形区接触特征的影响，提出了基于各向异性的接触压力模型[24-25]。
上述结果表明随着对变形区轮廓、界面摩擦条件和材料屈服特性认识的不断深入，薄带轧制变形区理论的计算精度不断提高，但各变形区理论适用范围的划分却十分模糊。为此笔者采用理论分析和数值模拟相结合的手段，开展了薄带轧制变形区接触特征变化规律及典型接触压力理论模型的适用性研究。研究结果可进一步加深对现有薄带轧制变形区理论的理解程度，并为选择更合适的理论模型提供理论指导和数据支撑。
1. 变形区接触压力模型理论分析
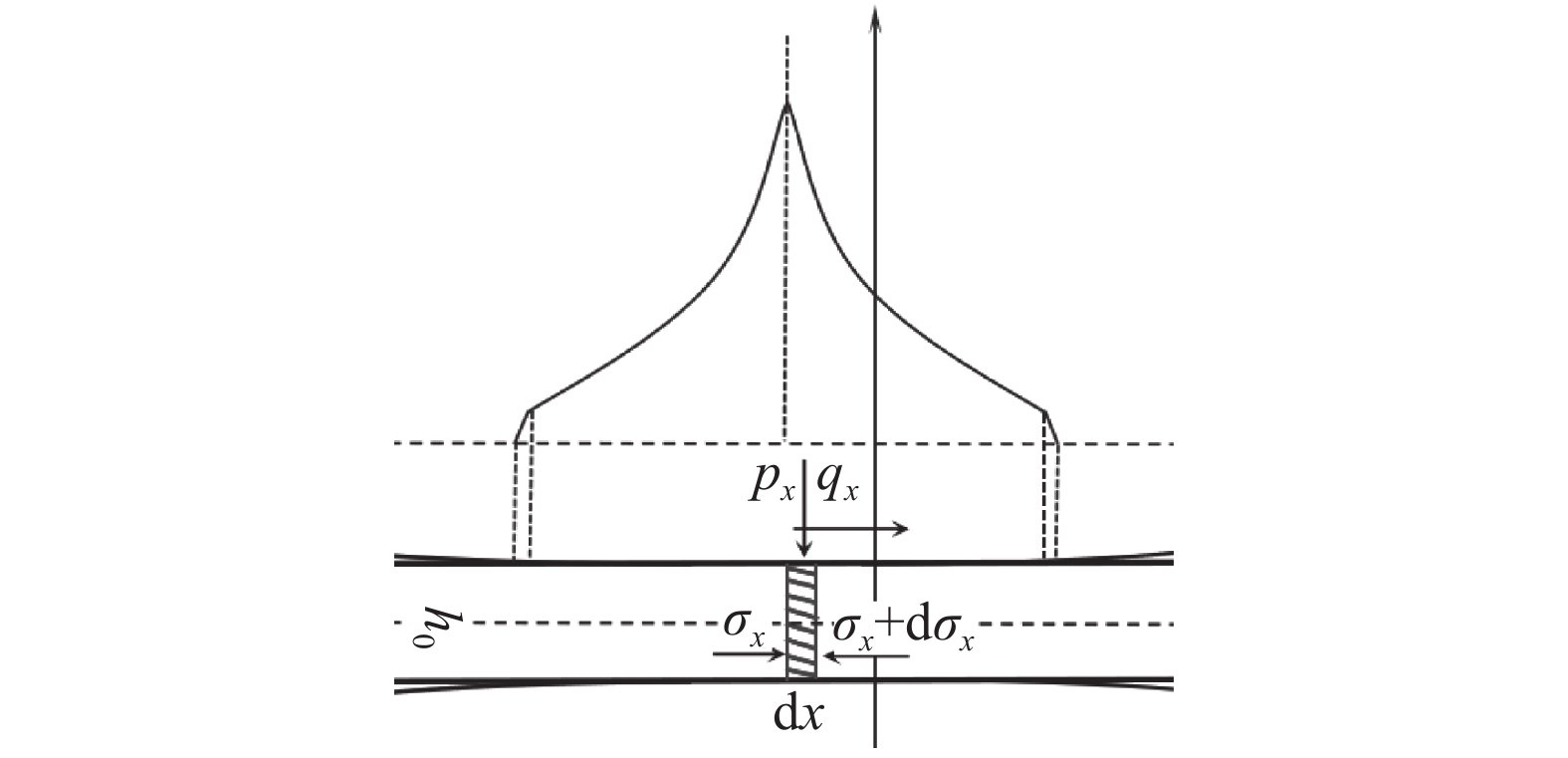
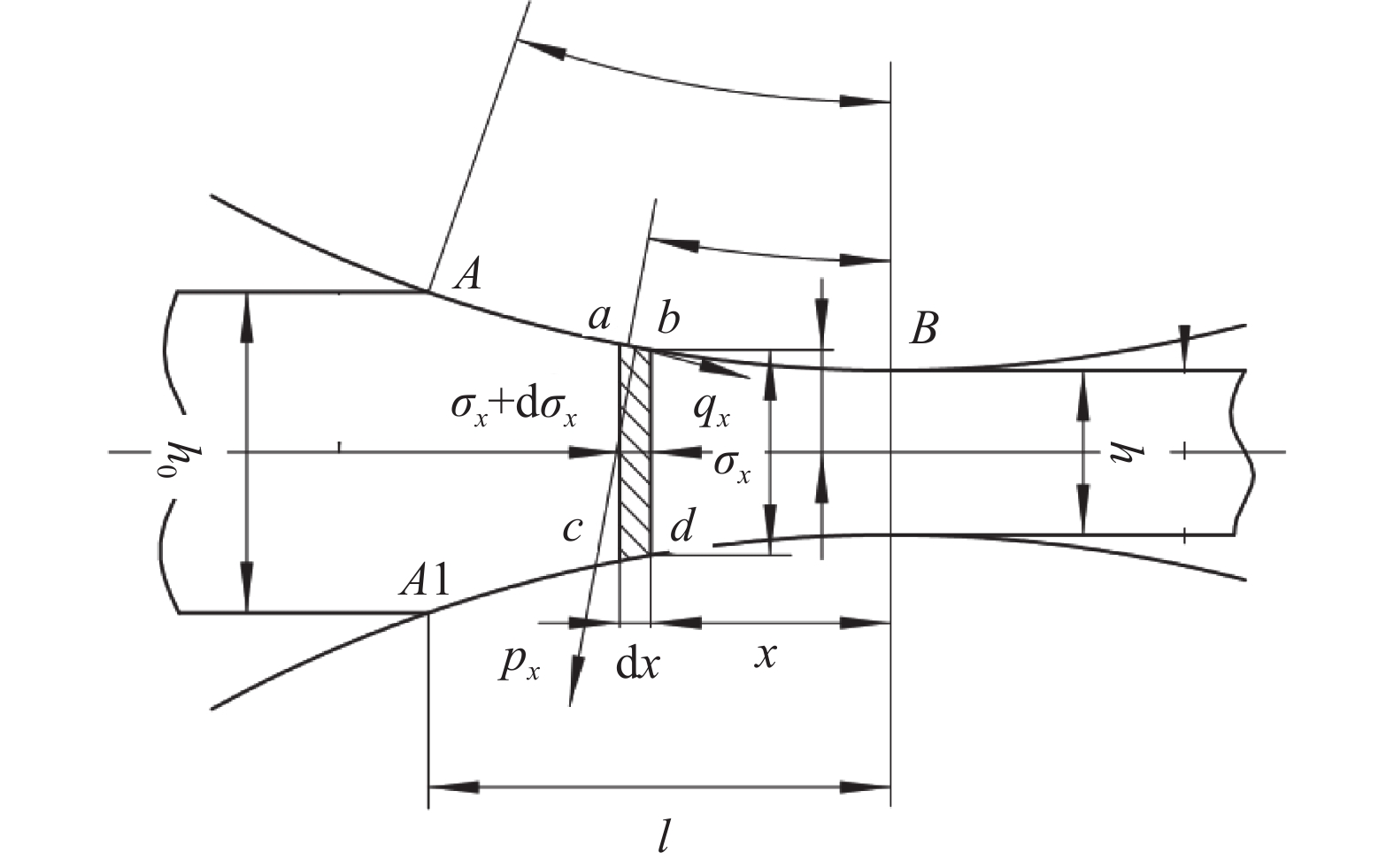
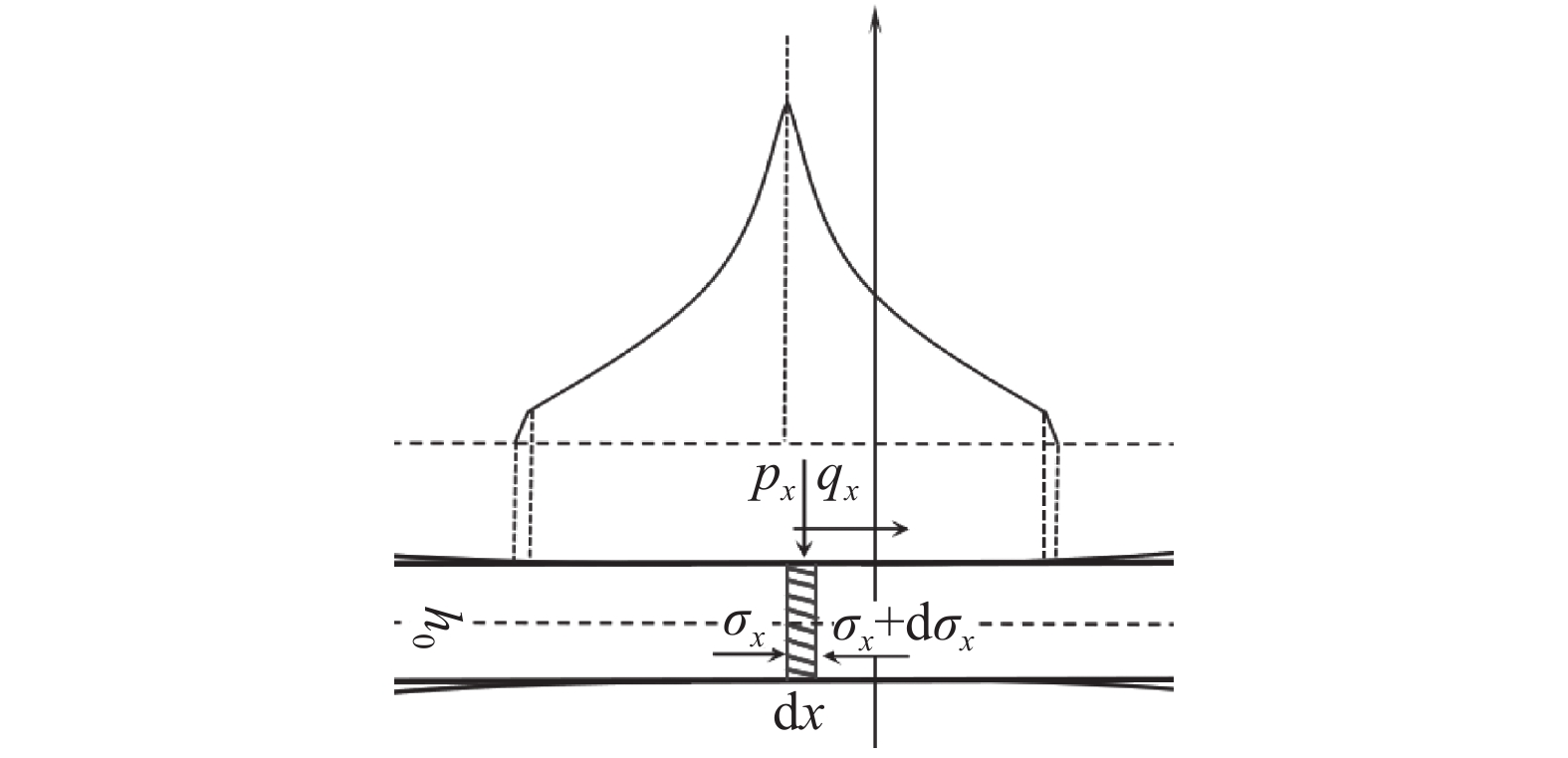
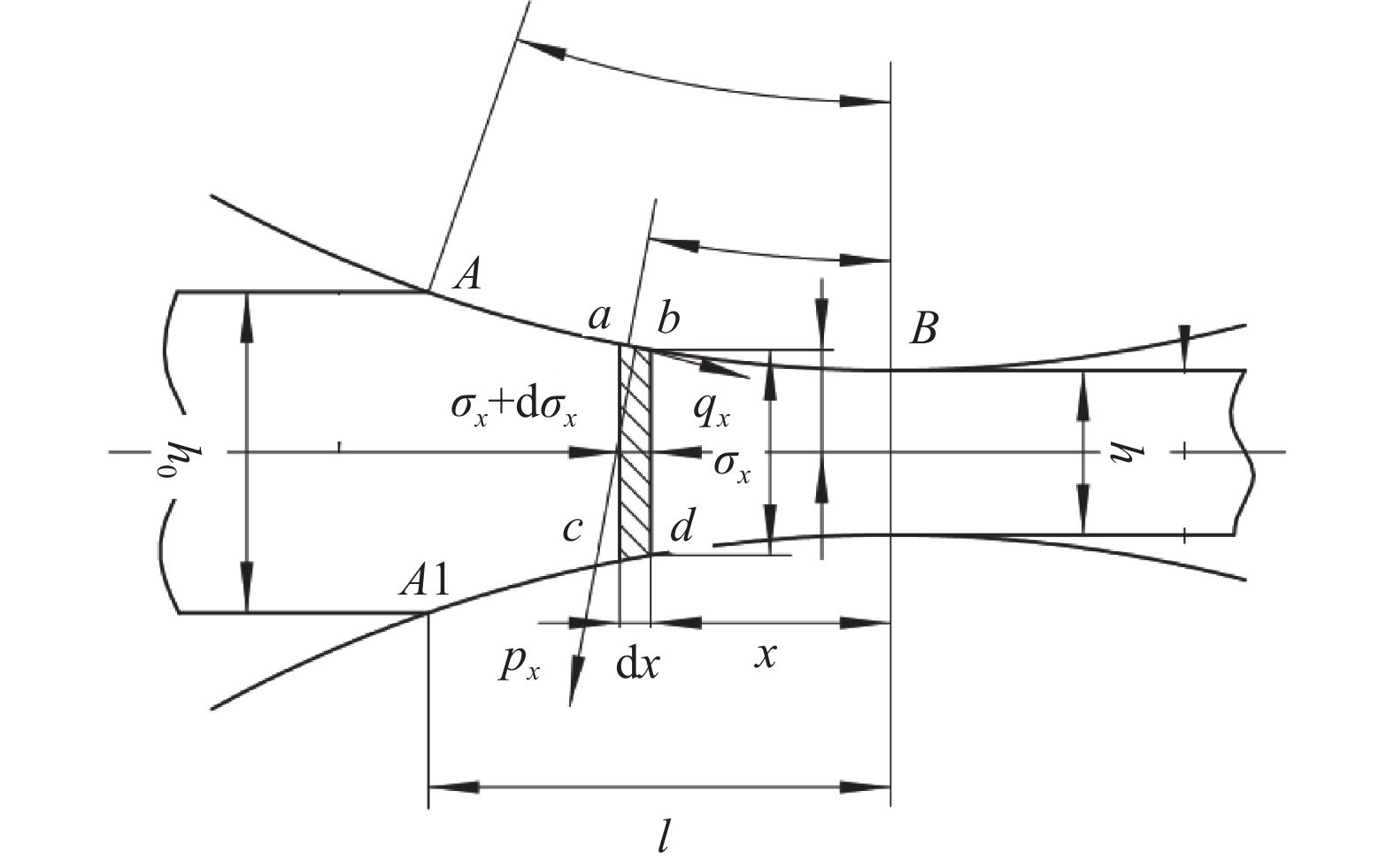
对于变形区形状系数远大于1的薄带轧制可将其简化为平面应变问题，图1为变形区微元体的受力示意。图1中σx为内应力，dσx为内应力增量，px为接触压力，qx为摩擦力，dx为微元体长度，h0为轧件初始厚度，l为接触弧长。
图 1 变形区微元体的受力示意Figure 1. Schematic diagram of applied force in the deformation zone microelement摩擦力qx在垂直方向上的分力相比接触压力甚小可忽略不计，则单位宽度轧制力pw可近似表示为：
$$ p_w=\int_0^lp_x\mathrm{d}x $$ (1) 由式(1)可知pw的计算主要受接触压力px和接触弧长l的影响，上述两者准确表达的关键在于对变形区轮廓的合理认识及对轧件弹塑性变形状态的准确判别，然而不同理论模型所得到的计算结果却存在显著差异，归因于各理论模型对变形区轮廓、界面摩擦条件和轧件弹塑性状态等的认识和假设条件的不同。下面简要介绍了三种典型模型的推导特点、成立的先决条件和主要表达式，并在此基础上对比分析了各理论模型的计算精度和适用区间。
1）全塑性-圆弧压扁增大形轮廓-Stone模型
图2为Stone模型变形区内微元体受力及接触压力分布示意，由图2可知接触压力曲线由变形区两侧向中心呈内凹形加速递增趋势。该模型假设：① 将薄板带轧制视为两个平板间的压缩；②轧辊弹性压扁后仍保持圆弧形轮廓，并采用Hitchcock公式计算接触弧长；③整个变形区内均满足库伦摩擦，轧件瞬时由塑性变形转变为弹性变形。
图 2 Stone模型变形区受力及接触压力分布示意Figure 2. Schematic diagram of force and contact pressure distribution in the deformation under Stone modelStone模型接触压力方程和Hitchcock半径增大形弧长公式为[8-9]：
$$ \left\{ \begin{array}{l} p_x=\left(1.155 \sigma_s-\sigma_T\right) \exp \left[\dfrac{2 f}{h_0}\left(x_B-x\right)\right] \\ l_2 = \sqrt{R \Delta h + \left[8 R \bar{p}\left(\dfrac{1 - v_R^2}{\pi E_R}\right)\right]^2} + 8 R \bar{p}\left(\dfrac{1 - v_R^2}{\pi E_R}\right) \end{array}\right. $$ (2) 其中，σs为轧件屈服强度；σT为平均张应力；f为摩擦系数；R为轧辊半径；$\bar p $为平均接触压力；ER和vR为轧辊弹性模量和泊松比；Δh为压下量。
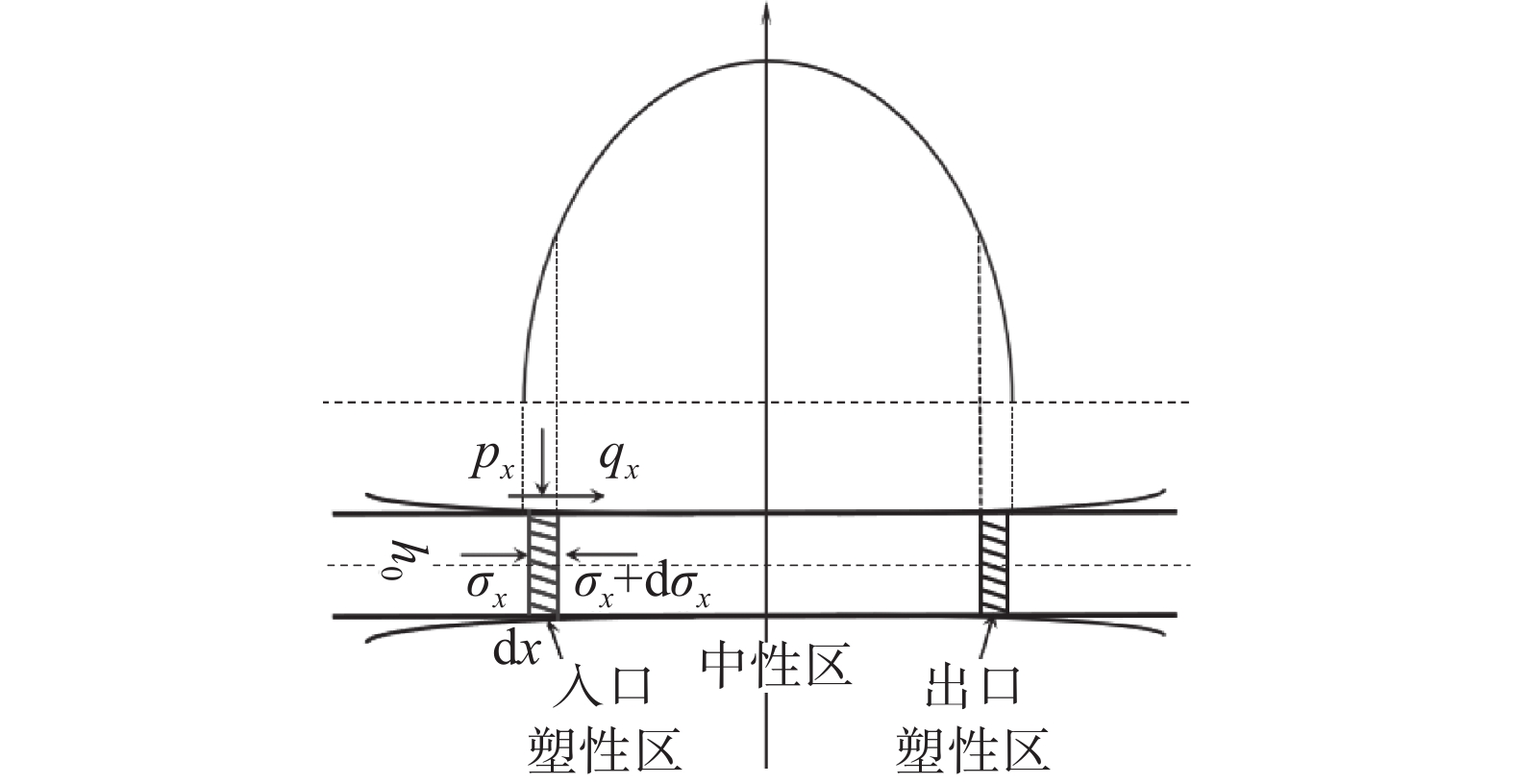
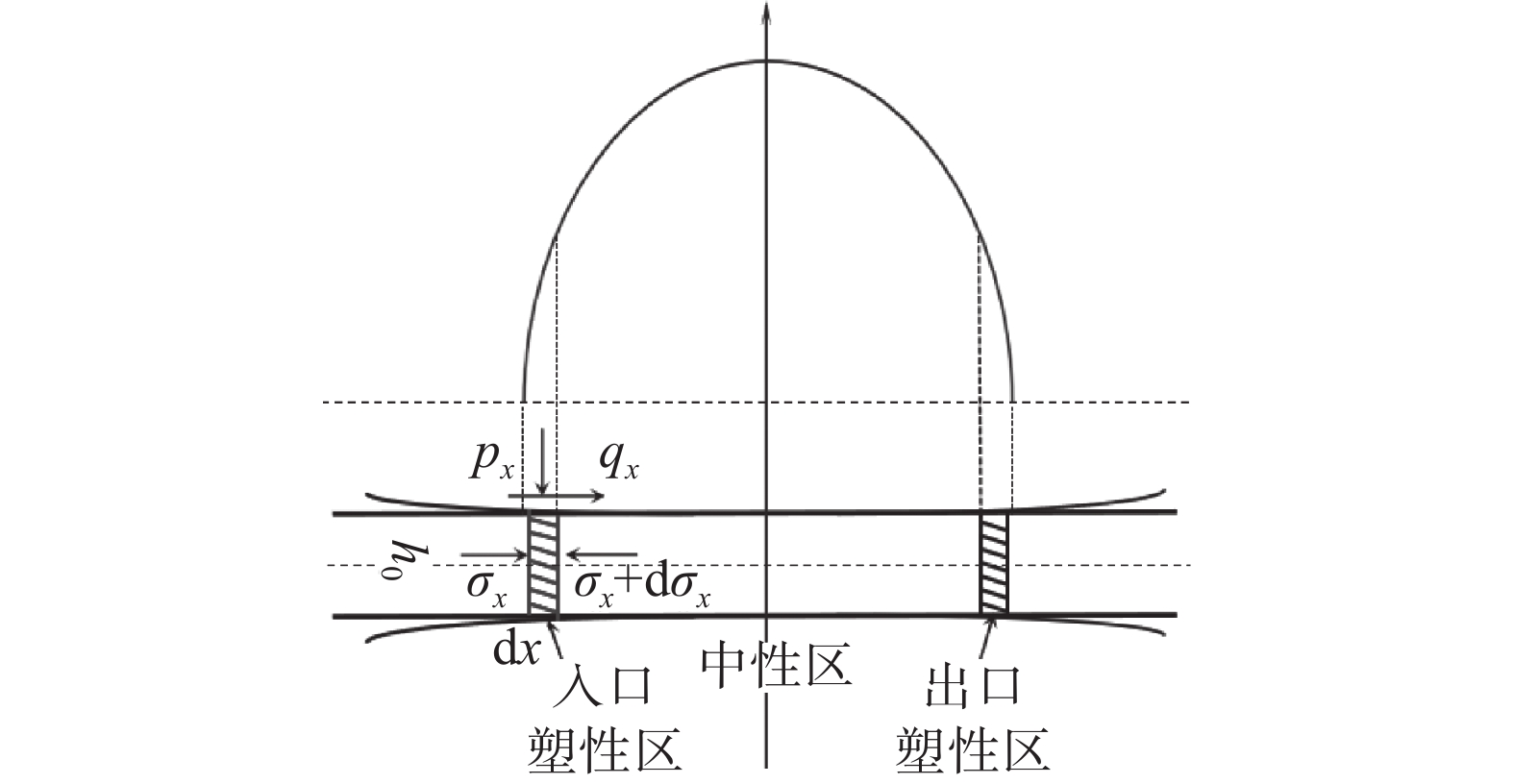
2）全弹性-近直线形轮廓-Johnson模型
图3为Johnson模型受力及接触压力分布示意，由图3可知接触压力曲线呈半椭圆形对称分布。该理论假设： ① 轧辊与轧件均以弹性变形为主，接触压力符合赫兹弹性理论；② 轧辊与轧件之间基本均为无相对滑移粘着区。
图 3 Johnson模型变形区受力及接触压力分布示意Figure 3. Schematic diagram of force and contact pressure distribution in the deformation zone under Johnson modelJohnson模型接触压力和接触弧长符合赫兹弹性理论[17]：
$$ \left\{\begin{array}{l} P(x)=\dfrac{2 p_w}{\pi a}\left[1-\left(\dfrac{x}{a}\right)^2\right]^{1 / 2} \\ a=\left(\dfrac{4\left(1-v^2\right) p_w R}{\pi E_R}\right)^{1 / 2} \end{array}\right. $$ (3) 其中，a为半接触弧长，x为轧件位置。
3）弹塑性-非圆弧形轮廓-组合型模型
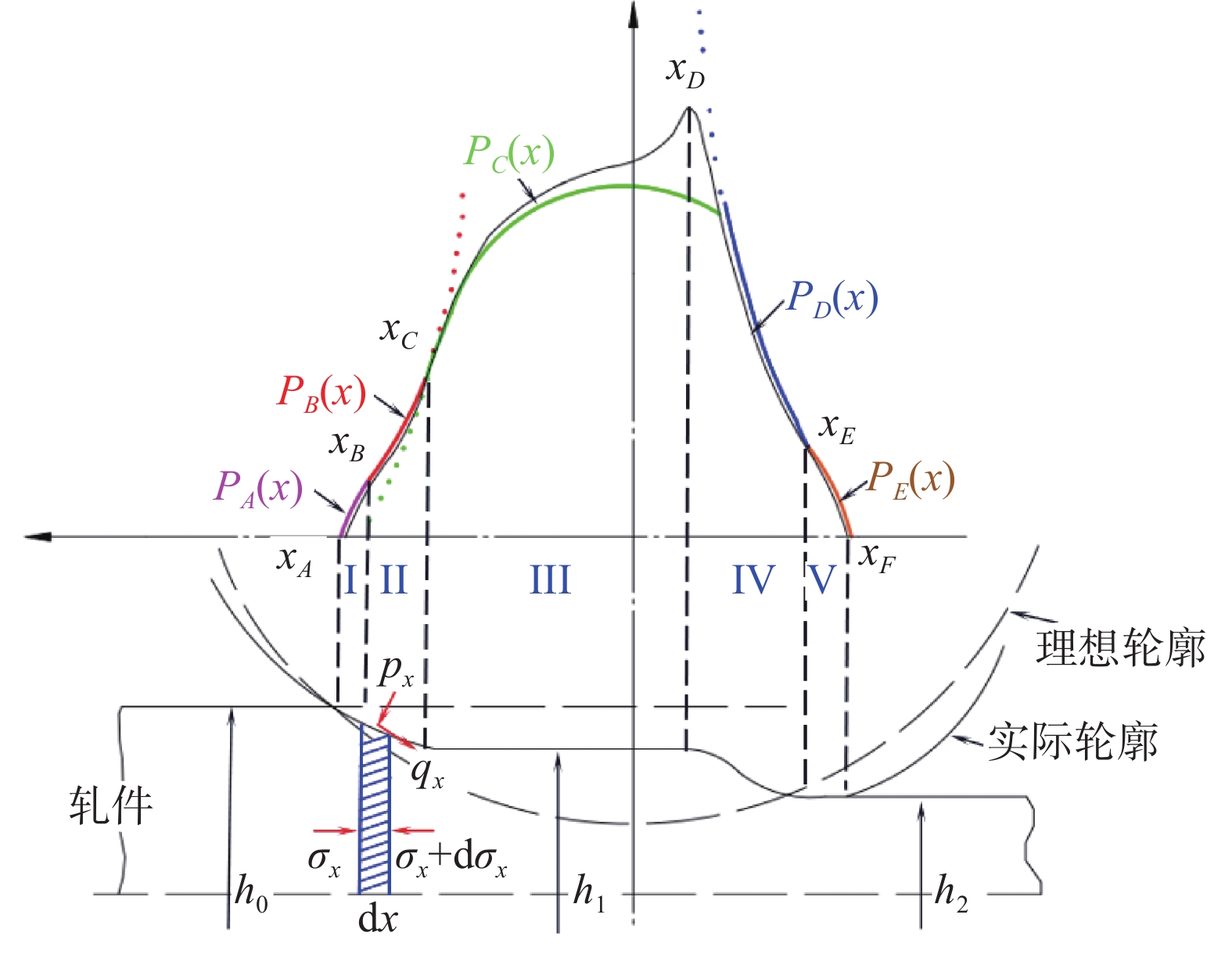
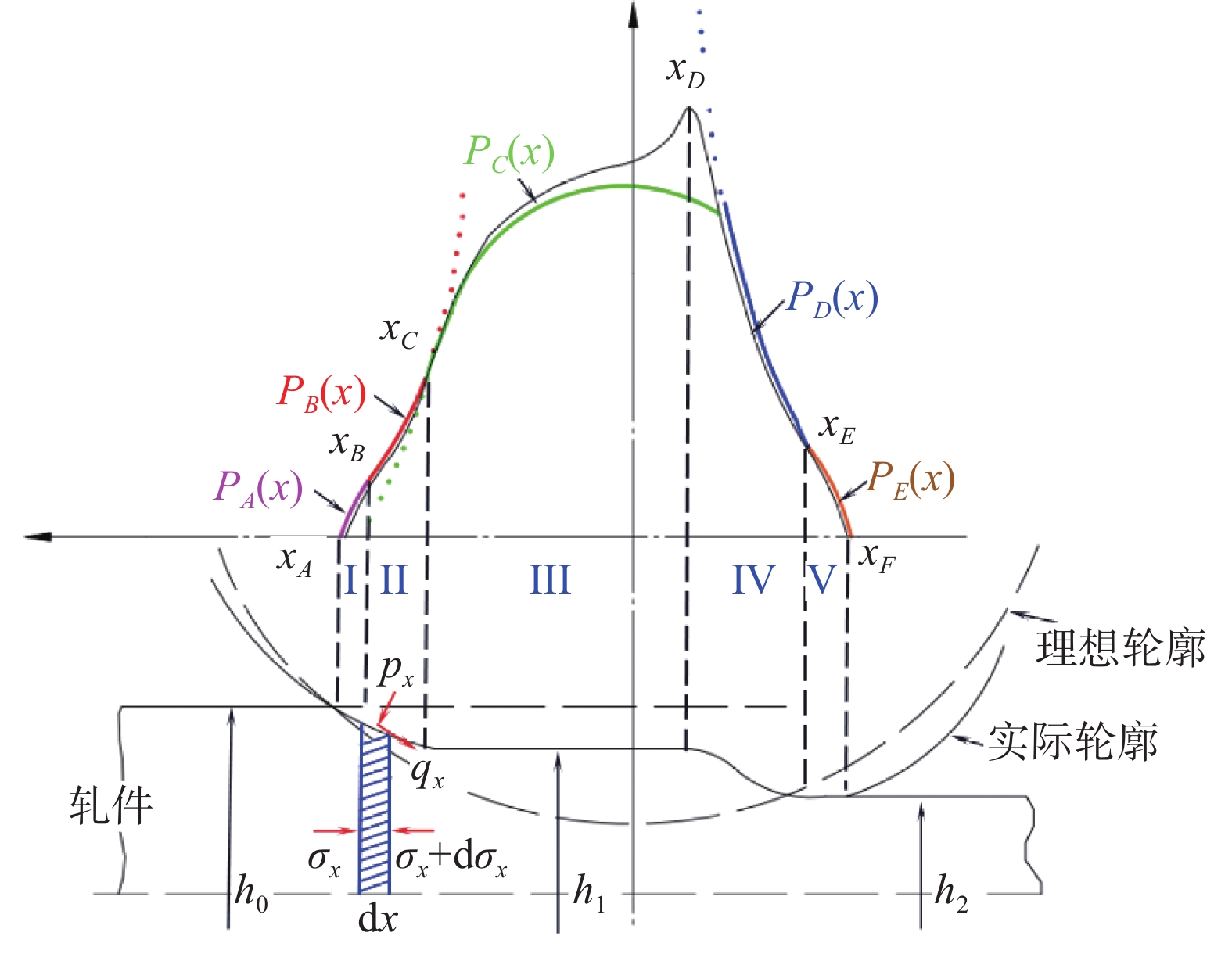
由Stone模型可知塑性区内接触压力曲线成内凹形加速递增，而轧辊弹性压扁区域内的接触压力曲线符合Johnson模型的半椭圆形分布，故结合上述两种理论模型的特点，在Fleck非圆弧形轮廓轧制模型基础上提出了简化后的组合型模型，如图4所示。由图4可知，依据轧辊轮廓和接触压力分布特点可对变形区进行划分，区域I、V分别为入口、出口弹性区，所对应的接触压力方程分别为PA(x)、PE(x)；区域II、IV分别为入口、出口塑性区，所对应的接触压力方程分别为PB(x)、PD(x)；区域III为中性区，所对应的接触压力方程为PC(x)。其中PC(x)忽略了出口塑性区尖锐再入角所导致的压力峰值，对于薄带轧制而言，此忽略在一定工艺下的影响程度是有限的，具体结果将在后续内容中说明。xA，xB，xC，xD，xE和xF分别对应各分区的临界点坐标，h0为轧件初始厚度，h1为中性区轧件厚度，h2为轧后厚度。
图 4 组合型模型变形区受力及接触压力分布示意Figure 4. Schematic diagram of the force and contact pressure distribution in the deformation zone under the combined model由图4可知，变形主要集中于入口塑性区II和出口塑性区IV，且入口塑性区II和中性区III内的接触压力曲线（PB(x)和PC(x)）在临界点xC处相切，xB和xE处也存在相似的规律，而xD处的接触压力峰值与出口塑性区尖锐的再入角有关。由于不同区域p(x)的分布状态和所采用描述其特点的函数不同，故可对变形区接触压力曲线进行分段计算，式(4)为组合后的单位压力公式。
$$ { P\left( x \right)\left\{ \begin{array}{*{20}{l}} {1.155{\sigma _{{\mathrm{eq}}}},}&{x \in \left[ {{x_A},{x_B}} \right)}\\ {\left( {1.155{\sigma _{{s_1}}} - {\sigma _T}} \right)\exp \left[ {\dfrac{{2f}}{{{h_0}}}\left( {{x_B} - x} \right)} \right],}&{x \in \left[ {{x_B},{x_C}} \right]}\\ {\dfrac{{2{p_w}}}{{\pi a}}{{\left[ {1 - {{\left( {\dfrac{x}{a}} \right)}^2}} \right]}^{1/2}}a = {{\left( {\dfrac{{4{p_w}R}}{{\pi {E^{*}}}}} \right)}^{1/2}},}&{x \in \left[ {{x_C},{x_D}} \right]}\\ \left( {1.155{\sigma _{{s_2}}} - {\sigma _T}} \right)\exp \left[ {\dfrac{{2f}}{{{h_1}}}\left( {{x_E} - x} \right)} \right],& x \in \left[ {{x_D},{x_E}} \right]\\ 1.155{\sigma _{{\mathrm{eq}}}},& x \in \left[ {{x_E},{x_F}} \right] \end{array} \right.} $$ (4) 以入口塑性区为例，xC处满足接触压力值及其导数值均相等的条件：
$$ P_{B}\left(x_{C}\right)=P_{C}\left(x_{C}\right) $$ (5) $$ \mathrm{d}P_B\left(x_C\right)/\mathrm{d}x=\mathrm{d}P_C\left(x_C\right)/\mathrm{d}x $$ (6) 将式(4)代入式(5)和式(6)中可得：
$$ \frac{2 p_{\mathrm{w}}}{\pi a}\left[1-\left(\frac{x_{C}}{a}\right)^{2}\right]^{1 / 2}=1.155 \sigma_{s} \exp \left[\frac{2 f}{h_{0}}\left(x_{B}-x_{C}\right)\right] $$ (7) $$ \begin{split} & \frac{2p_{\mathrm{w}}}{\pi a}\left(-\frac{x_C}{a^2}\right)\left[1-\left(\frac{x_C}{a}\right)^2\right]^{-1/2}=1.155\sigma_s \\ & \qquad\left(-\frac{2f}{h_0}\right)\exp\left[\frac{2f}{h_0}\left(x_B-x_C\right)\right] \end{split} $$ (8) 由式(7)和式(8)等号左侧两式比值关系与等号右侧两式比值关系相等可得：
$$ \frac{\mathrm{d}P_B\left(x_c\right)}{P_B\left(x_c\right)}=\frac{\mathrm{d}P_C\left(x_c\right)}{P_C\left(x_c\right)} $$ (9) 求解可得xC为：
$$ x_c=\frac{\sqrt{h_0^2+16a^2f^2}-h_0}{4f} $$ (10) 联立式(4)和式(10)可得xB：
$$ x_{B}=x_{c}+\frac{h_{0}}{2 f} \ln \left\{\dfrac{2 p_{w}\left[1-\left(\dfrac{x_{c}}{a}\right)^{2}\right]^{1 / 2}}{1.155 \sigma_{s} \pi a}\right\} $$ (11) 由式(11)可发现在已知轧辊的材料参数E和v、初始薄带厚度h0和接触界面摩擦系数f的情况下，入口塑性区结束点坐标xC与等效半接触弧长a相关。出口侧xD处坐标通过PC(xD)=PD(xD)确定，组合型模型所得xD临界点坐标会因接触压力尖锐峰值被忽略的影响而导致其略微偏离轧辊中心线，但其整体上影响程度有限，且会随薄带厚度的减小而不断减弱，而xE处坐标求解方法与入口塑性区一致。由于现实轧制过程中无法获得变形区内具体分区，故直接将整个变形区的接触压力积分所获得的单位宽度轧制力代入上式求得等效接触弧长2a的近似值，对于薄带轧制而言，其所造成的误差极小。
虽然上述三种模型推导的基本思路均为在变形区内提取微分体进行受力分析并建立平衡微分方程，在附加一系列假设前提下运用Tresca塑性方程、接触弧长方程、库伦摩擦条件和边界条件推导并求解变形区单位压力方程，但是对变形区接触特征认识的差异导致各理论模型的推导基础和成立先决条件存在显著差异，下面进一步对比分析了各理论模型在预测变形区接触特征时的计算精度和适用区间。
2. 轧制过程有限元模拟
2.1 有限元模型建立
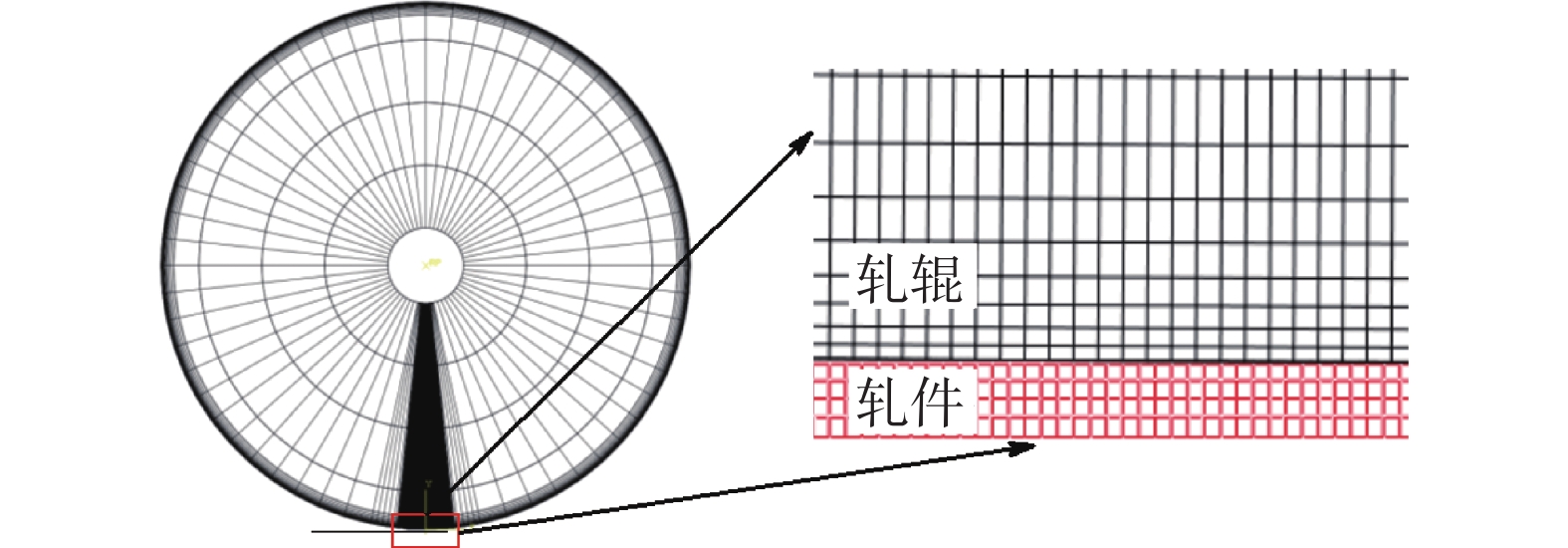
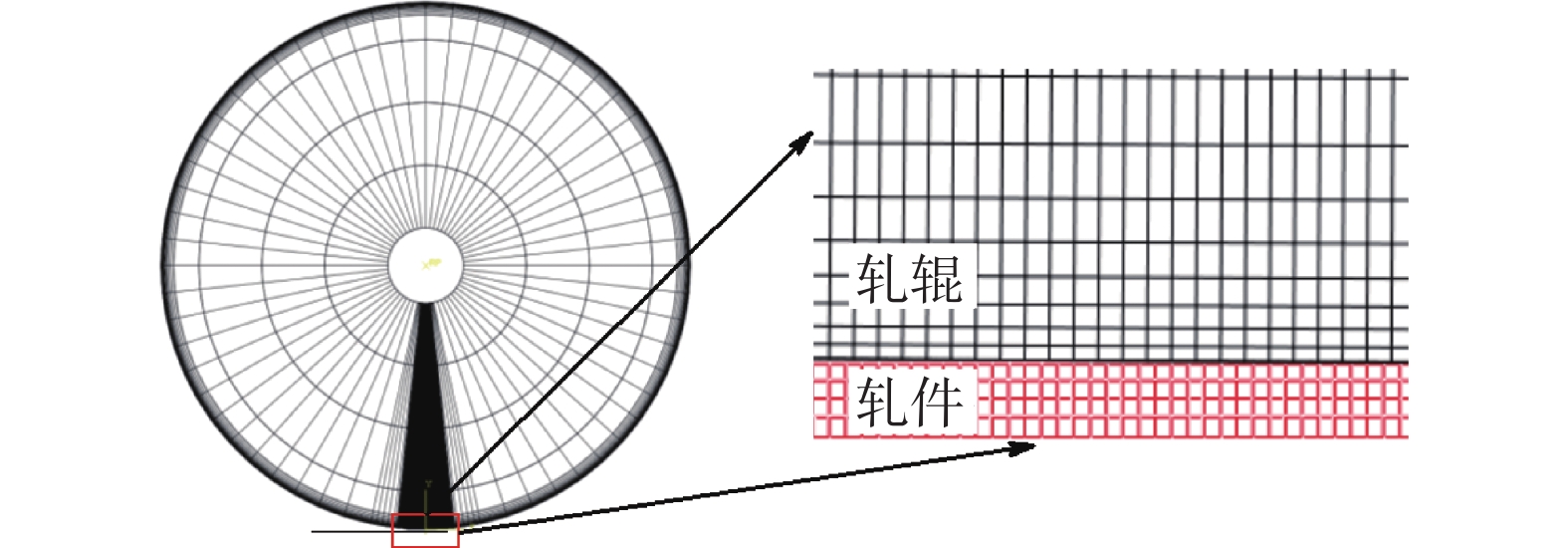
薄带轧制过程往往简化为平面应变问题进行分析，图5为关于中间水平面对称分布的二维弹塑性模型，具体建模过程及材料参数可参考文献[23,25]。为从理论角度探究薄带轧制过程中变形区特征的共性问题及随轧制工艺的变化规律，选取了如表1所示的轧制工艺。采用薄带厚度h0-预设压下率y的形式对轧制工艺进行命名。
表 1 薄带轧制工艺参数Table 1. Thin strip rolling process parameters薄带初始厚度h0 /mm 预设压下率y/% 0.3、0.2、0.1、0.075、0.05、0.03、0.02 20、40、60、80、100 2.2 仿真结果分析
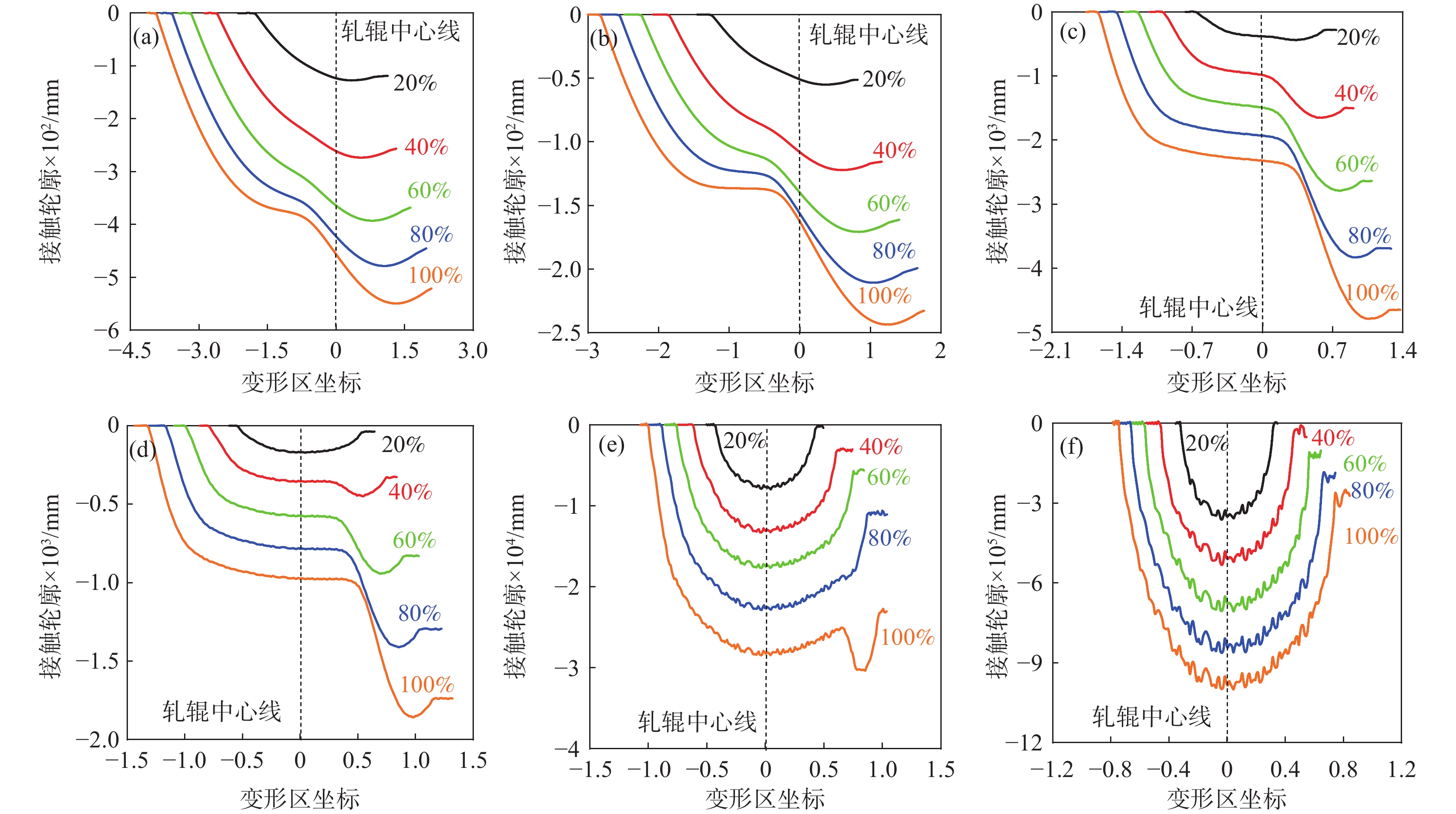
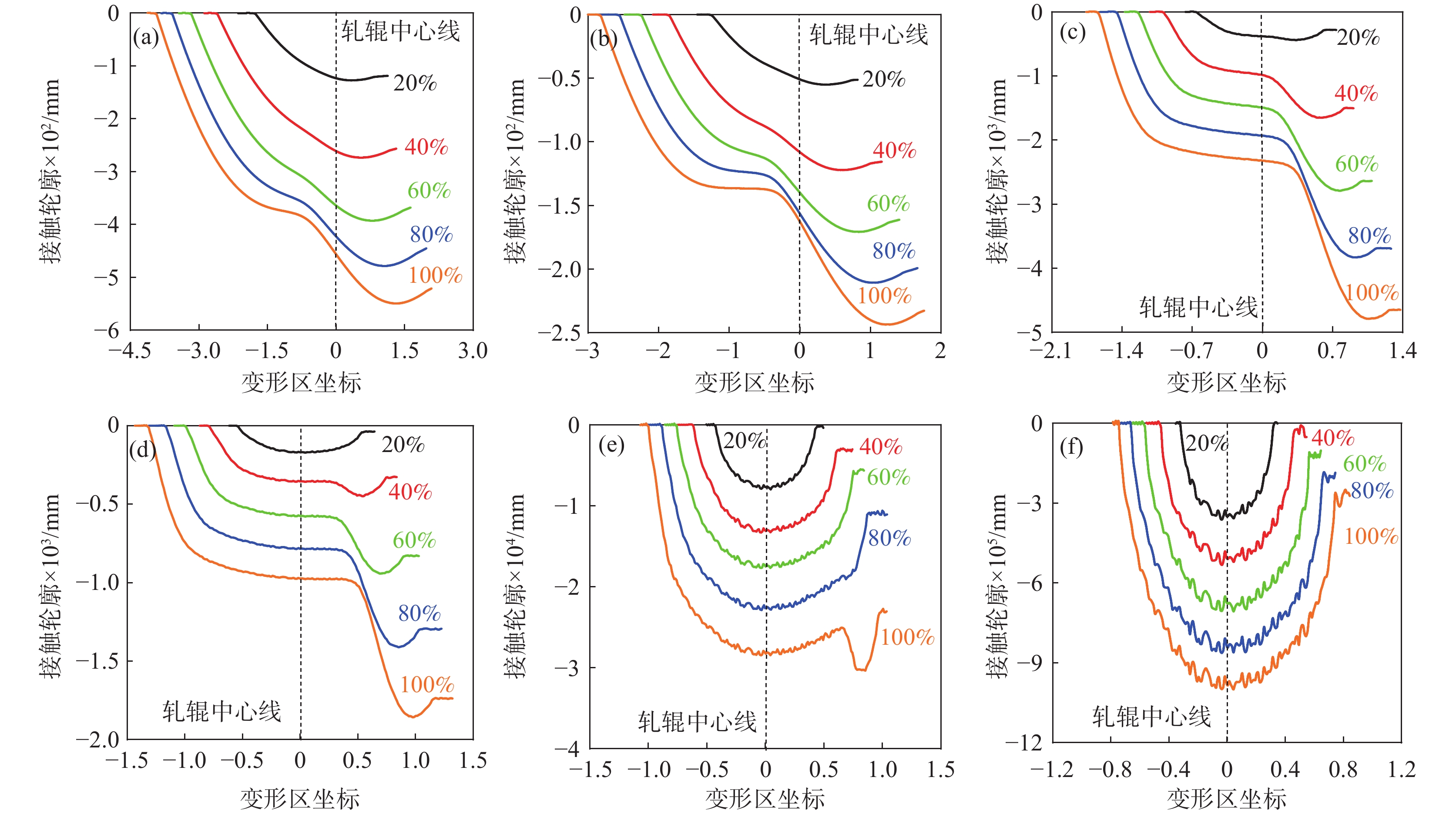
图6为变形区接触轮廓随薄带厚度和预设压下率的变化规律，以0.3～0.2 mm为例，随着预设压下率的增加，变形区接触轮廓依次经历了圆弧形—圆弧压扁增大形—非圆弧形，中性区的出现和所占变形区长度比例的增加导致变形区呈现出越来越明显的三阶段趋势。中性区首先出现在轧辊中心线左侧（入口侧），并随轧制工艺的变化而逐渐向出口侧扩展，且中性区内轧件压下幅度极小；中性区出现时所需预设压下率随薄带厚度的减小而不断降低，如0.3 mm−60%、0.2 mm−40%、0.1 mm−20%，0.075 mm−20%时只有弹性变形，而0.03 mm时变形区轮廓近似直线；相同预设压下率时中性区长度所占变形区比例随薄带厚度的减小而不断增加，所对应的入口和出口塑性区占比不断减小，进而出现预设压下率增加而实际压下率变化越来越小的现象。除此之外，由0.05 mm−80%～100%可发现出口塑性区先于入口塑性区消失，即入口塑性区是实现薄带塑性压下的前提。
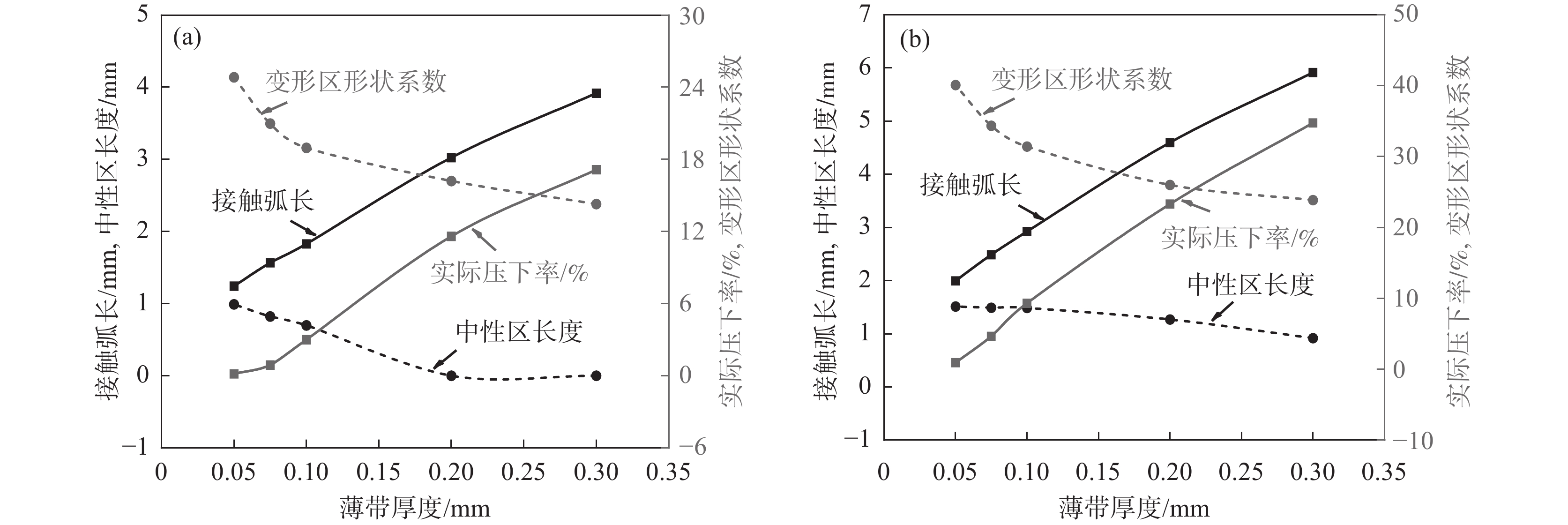
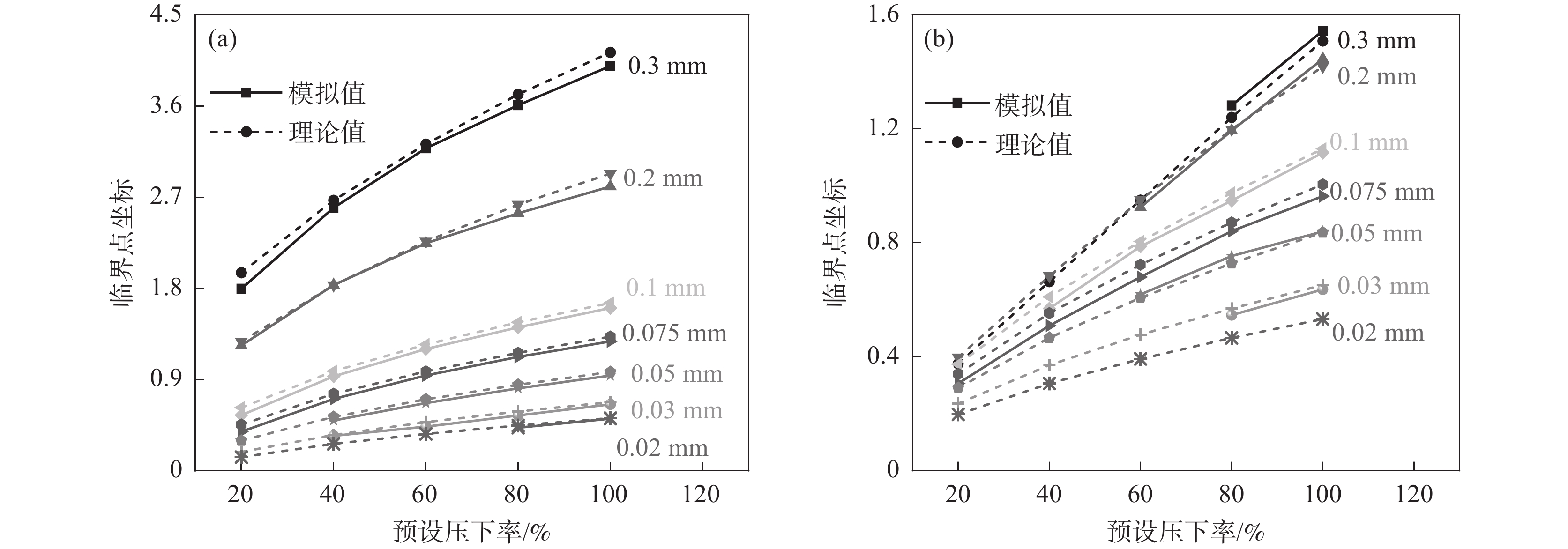
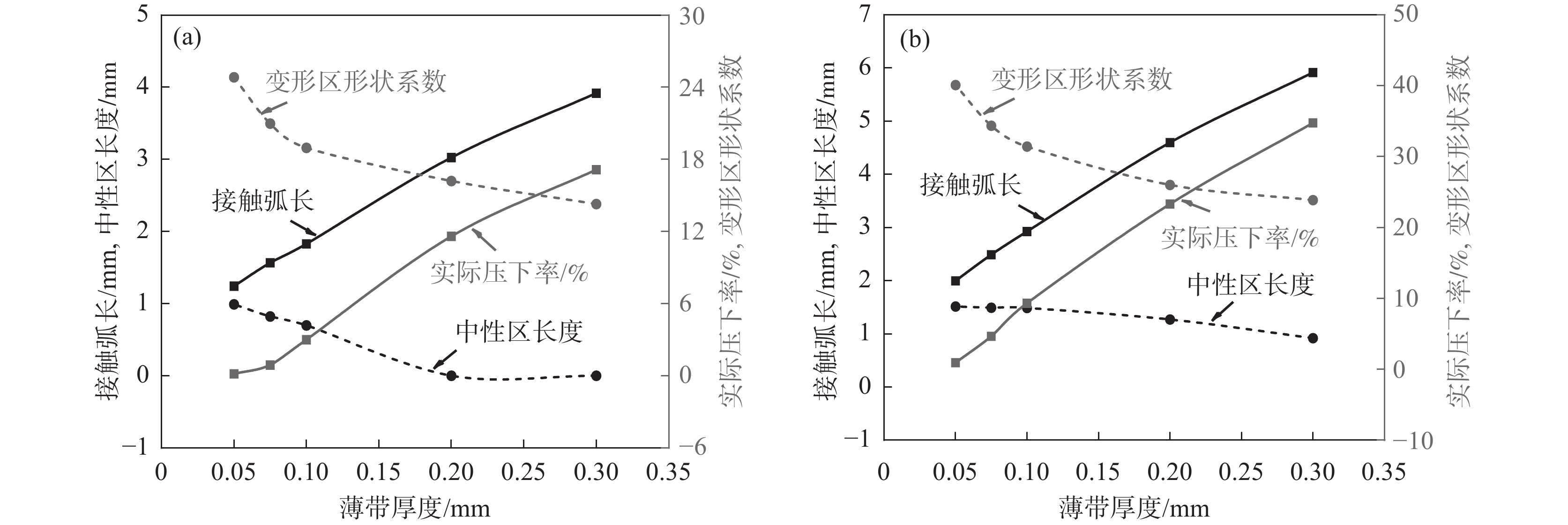
图 6 不同厚度薄带的变形区接触轮廓随压下率的变化(a) 0.3 mm；(b) 0.2 mm；(c) 0.1 mm；(d) 0.075 mm；(e) 0.05 mm；(f) 0.03 mmFigure 6. The contact profile of the deformation zone under different thicknesses thin strips with reduction ratio图7为接触弧长、中性区长度、实际压下率和变形区形状系数等随预设压下率和薄带厚度变化的规律。由图7可知，虽然接触弧长随薄带厚度的减小在变小，但中性区出现后其所占接触弧长长度比例随薄带厚度减小和预设压下率增加而不断增大，变形区形状系数（接触弧长与薄带厚度的比值）也表现出相似的变化规律，尤其0.1 mm以下时其增大速率明显加快。变形区形状系数的快增说明此时接触弧长的减小幅度相对于薄带厚度而言明显减小，显然中性区的出现导致接触弧长的减小速度变缓，上述现象也导致了轧件越薄越难轧的现象。
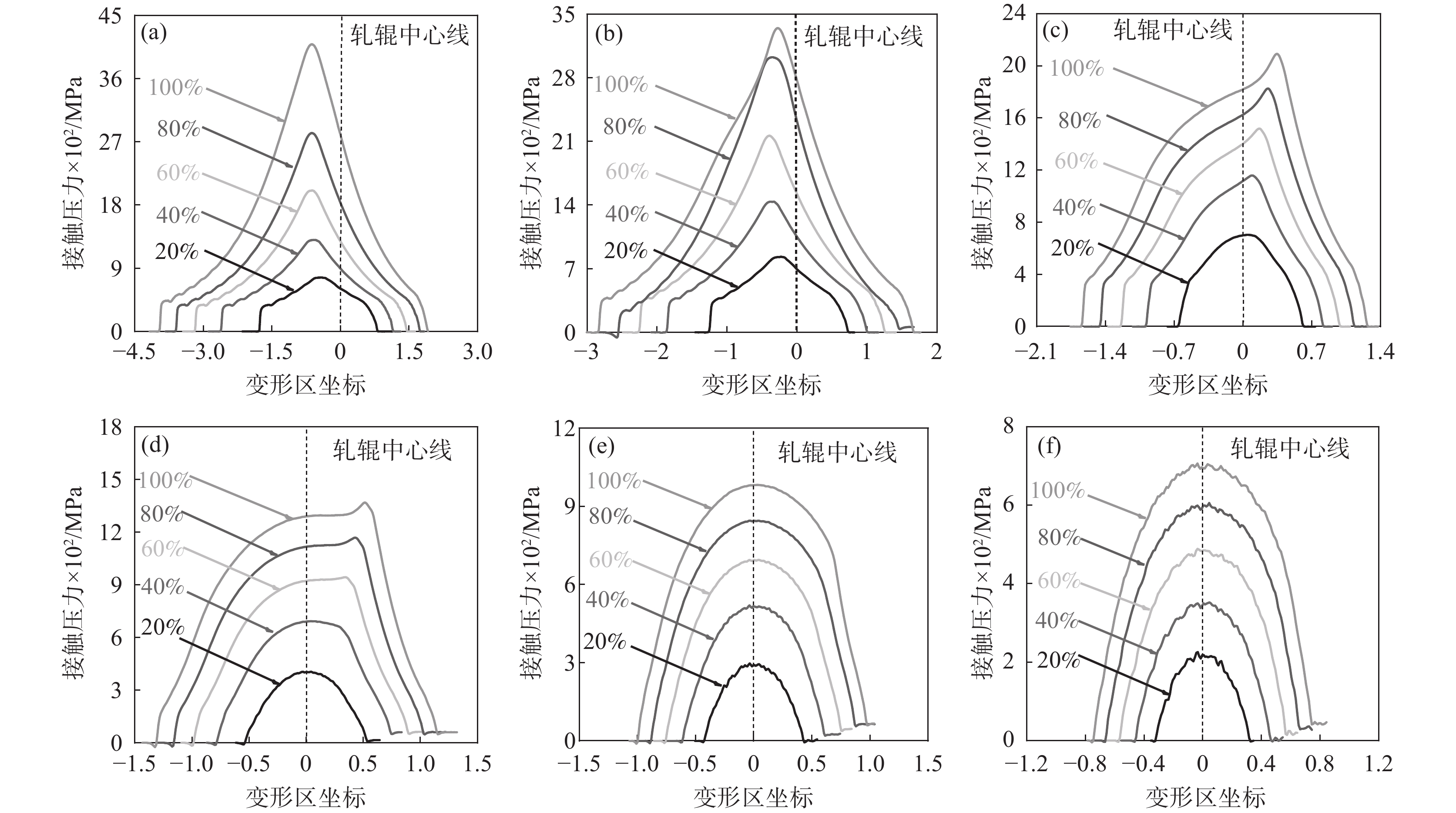
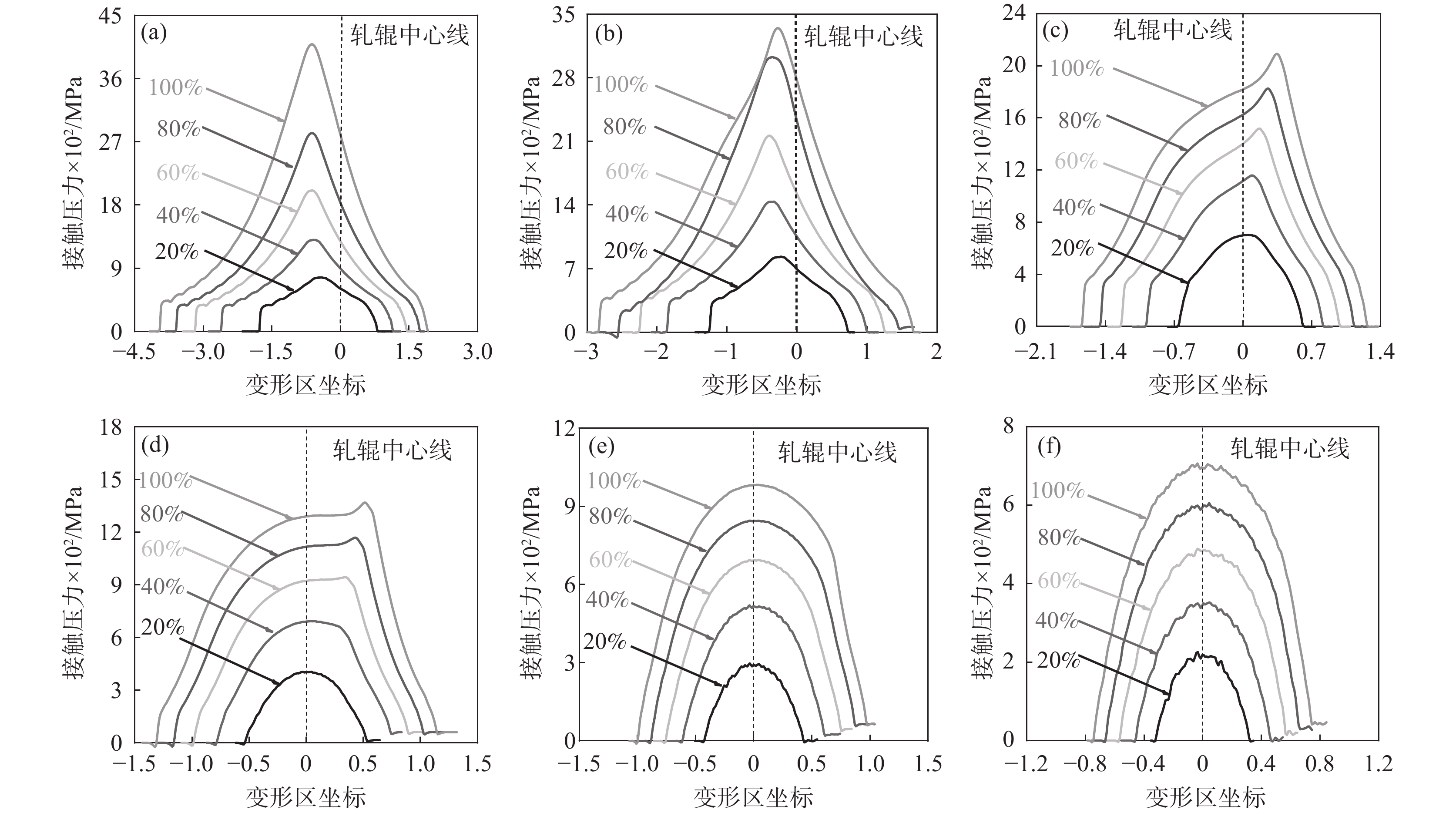
图 7 变形区接触特征随薄带厚度的变化规律(a) 预设压下率40%；(b) 预设压下率100%Figure 7. The variation of the contact characteristics in deformation zone with thin strip thickness图8为变形区接触压力随薄带厚度和预设压下率变化的规律，结合图6接触轮廓进行进一步分析。由图8可知，0.3～0.2 mm时接触压力存在明显峰值，且变形区接触压力曲线基本关于峰值应力呈左右对称分布的内凹形单调递增/递减趋势，而此厚度下以塑性变形为主，显然更加符合Stone模型；0.1～0.075 mm时接触压力曲线呈现明显的分段变化特征，入口塑性区内为内凹形加速递增（出口侧类似），中性区内为外凸形减速递增，而压力峰值与中性区—出口塑性区间尖锐的再入角有关，由非圆弧形接触轮廓和分段接触压力曲线可得此时更加符合组合型模型；0.05～0.03 mm时接触压力越来越接近半椭圆形分布，结合图6可知此厚度时塑性变形量与弹性变形量处于同一或者相近的数量级上，轧件主要以弹性变形为主，故更加符合Johnson模型。
图 8 不同厚度薄带的变形区接触压力(a) 0.3 mm； (b) 0.2 mm；(c) 0.1 mm；(d) 0.075 mm；(e) 0.05 mm；(f) 0.03 mmFigure 8. The contact pressure of the deformation zone under different thicknesses thin strips3. 变形区接触压力模型适用性分析
3.1 变形区接触弧长对比
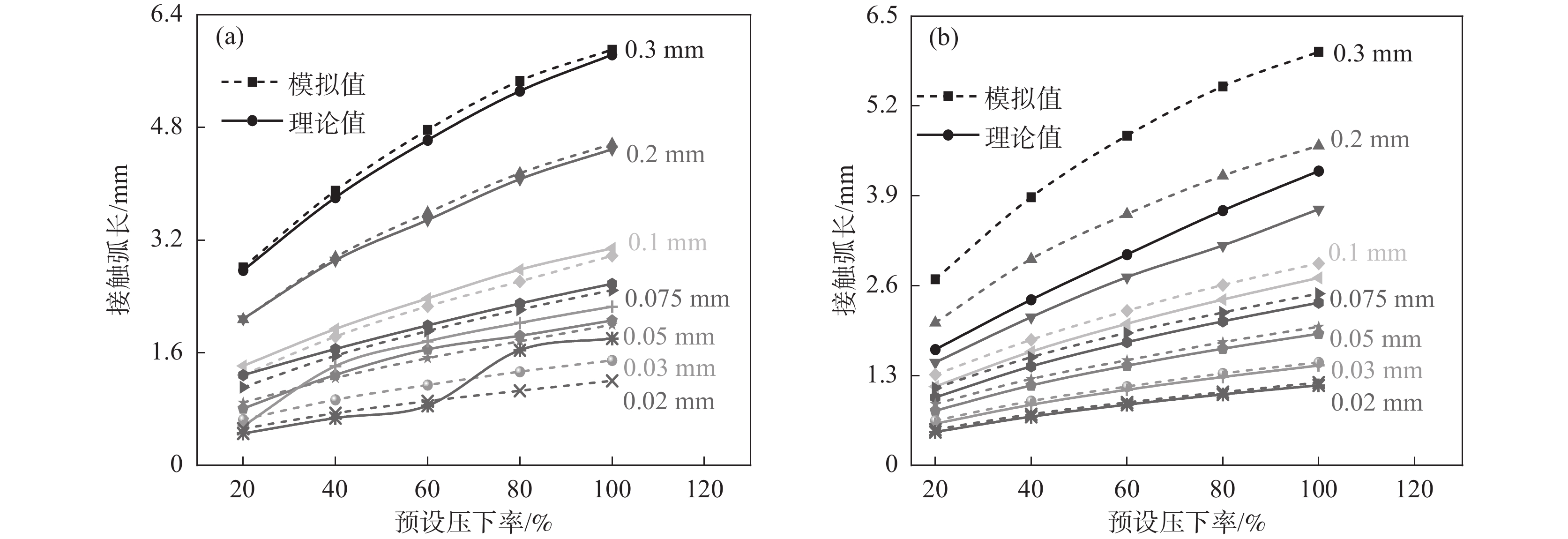
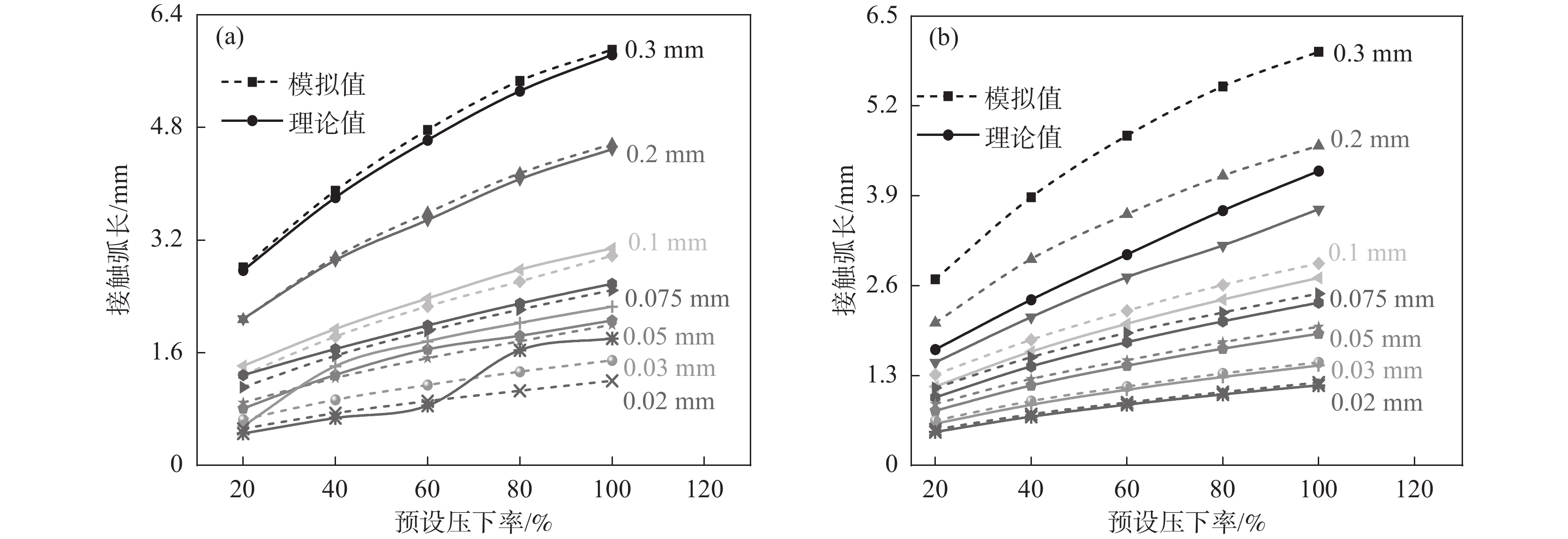
图9为接触弧长的模拟值与Hitchcock和Johnson理论值对比图(f=0.1)，由图9可知，0.075 ～ 0.3 mm时Hitchcock理论值与模拟值之间的吻合度较高，但小于0.05 mm时其误差程度明显随着薄带厚度的减小在不断增大；而Johnson模型理论值与模拟值的吻合程度随薄带厚度的减小而不断升高，小于0.075 mm时基本重合。结合图5和图8结果可知0.075 mm以上时变形区内塑性区占比随薄带厚度的增加而不断变大，此时Hitchcock弧长公式较符合；而0.075 mm以下时弹性区占比随薄带厚度减小而不断变大，此时Johnson模型预测精度更高。
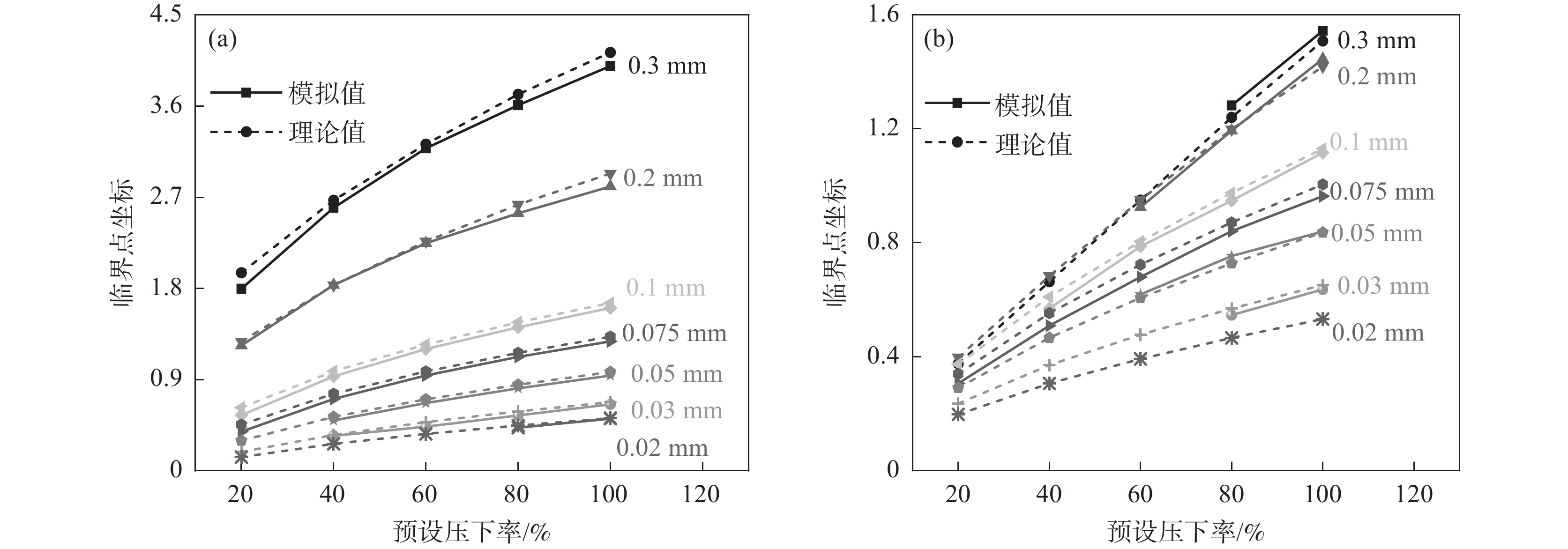
图 9 接触弧长的模拟值与Hitchcock和Johnson理论值对比(a) Hitchcock理论值；(b) Johnson理论值Figure 9. Comparison of the contact arc length from FE simulation and Hitchcock & Johnson models由图4可知变形区接触特征及弹塑性状态转变的判别与各分区临界点坐标密切相关，故图10中对比了入口塑性区起始点xB和中性区起始点xC的组合型模型理论值与模拟值的区别。同理，根据轧件出口厚度可得出口塑性区的临界点坐标，进而根据坐标可进一步计算出整个变形区或各分区的接触弧长。由图10可知xB的理论值与模拟值在薄带厚度较大的0.3～0.2 mm时的预测差值相对较大，但整体上吻合度较高且预测精度随薄带厚度的减小而升高；xC的理论值与模拟值吻合度也较高，但对于厚度较大的薄带没有中性区，而对于厚度极小的薄带基本不存在塑性区，显然此时的组合型模型并不理想。
图 10 入口塑性区临界点的模拟值与组合模型理论值对比(a) xB ；(b) xCFigure 10. Comparison of critical point of the plastic zone at the inlet from FE simulation and combined model3.2 变形区接触压力对比
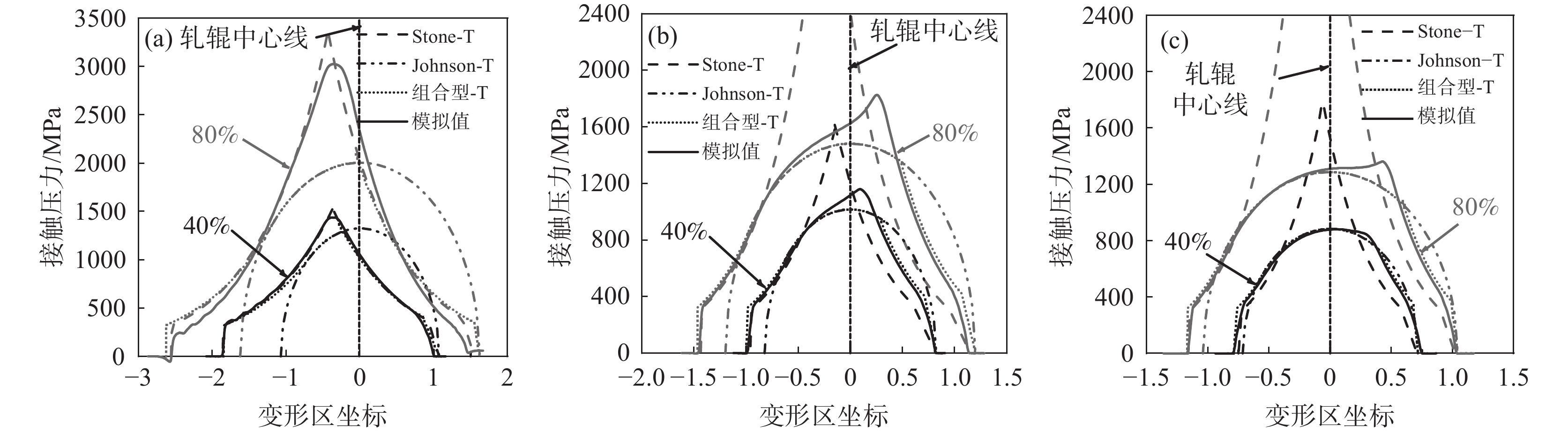
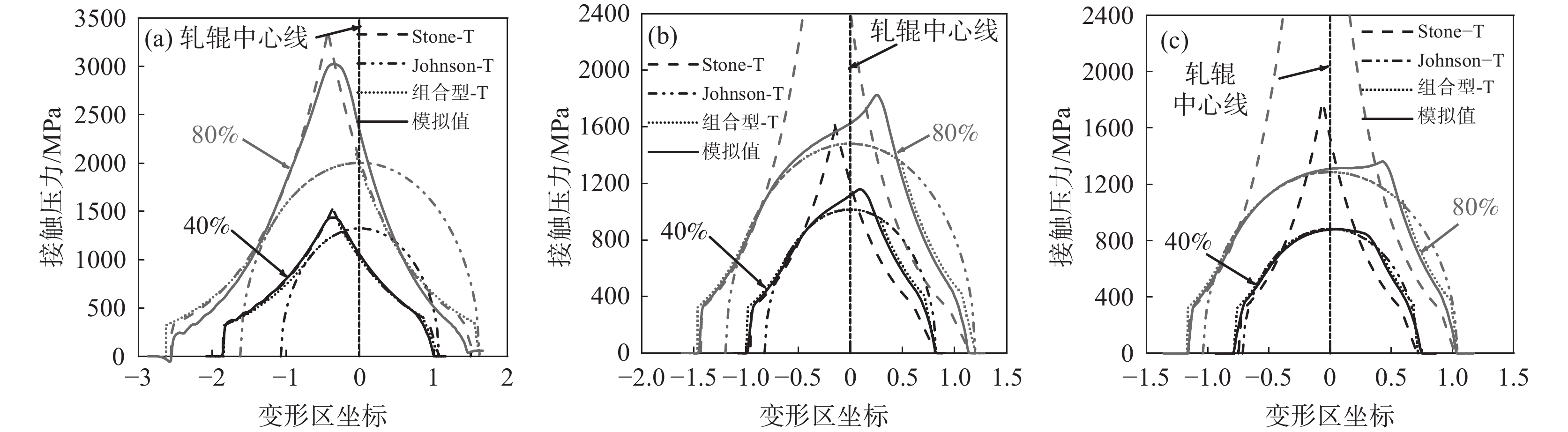
图11为变形区接触压力曲线模拟值与三种模型理论值的对比图，图中实线为模拟值(S)，虚线为理论值(T)。由图11可知，对于变形区接触压力曲线以呈内凹形为主的0.2 mm薄带而言，y=40%时Stone模型和组合型模型预测精度要高于Johnson模型，而y=80%时Stone模型的预测精度要明显高于Johnson模型和组合型模型。对于0.075 mm薄带而言，y=40%时组合型模型和Johnson模型的预测精度高于Stone模型，而y=80%时组合型模型接触压力曲线的贴合度明显高于另外两种模型；Johnson理论值与模拟值的区别主要集中于入口塑性区和出口塑性区，归因于此厚度时存在入口和出口塑性区，全弹性假设在此区段内并不适用。对于变形区内中性区和塑性区长度占比差异较小的0.1 mm薄带，三种模型的预测精度介于0.2 mm和0.075 mm之间，也更准确地体现了组合型模型理论值与模拟值曲线之间的贴合程度。
图 11 接触压力模拟值与三种模型理论值对比(a) 0.2 mm；(b) 0.1 mm；(c) 0.075 mmFigure 11. Comparison of contact pressures from FE and three models除此之外，由图11也可发现对于0.1 mm及以下厚度薄带压力峰值占整个变形区的比例较小，且占比随薄带厚度的减小在不断降低，故组合型接触压力模型理论分析时忽略中性区与出口塑性区尖锐压力峰值是可行的。综上三种厚度薄带对比可发现对于厚度较大且压下率较大时的薄带轧制变形区接触特征的预测优选Stone模型，此时塑性变形为主；薄带厚度较小或压下率较小时Johnson模型的预测精度较高，且吻合度随薄带厚度的减小而不断增加，此时弹性变形为主；而组合型模型的适用范围介于两者之间，此时变形区内塑性变形和弹性变形处于相近的数量级。
表2为单位宽度轧制力模拟值与组合型模型和Stone模型理论值之间的相对误差，此处选择了具有代表性的0.2、0.1、0.075 mm进行说明。由表2可知，组合型模型在0.2 mm-100%～20%、0.1 mm-100%～40%和0.075 mm-100%～80%时的预测误差随薄带厚度和预设压下率的增加而不断减小，但0.1 mm-40%～20%和0.075 mm-80%～20%时的误差程度却在不断变大，因此组合型模型并不适用于以弹性变形为主的情况（极薄或弹性变形为主）。然而Stone模型的预测误差却随薄带厚度的减小和预设压下率的增加而急剧增大，如由0.2 mm-100%时的10.151%增加至0.075 mm-100%时的109.424%，显然该模型并不适用于极薄带轧制变形区接触特征的预测。两种模型对比可发现0.2 mm时Stone模型的误差程度要比组合模型小，说明此厚度时Stone模型比组合型模型更加适合。
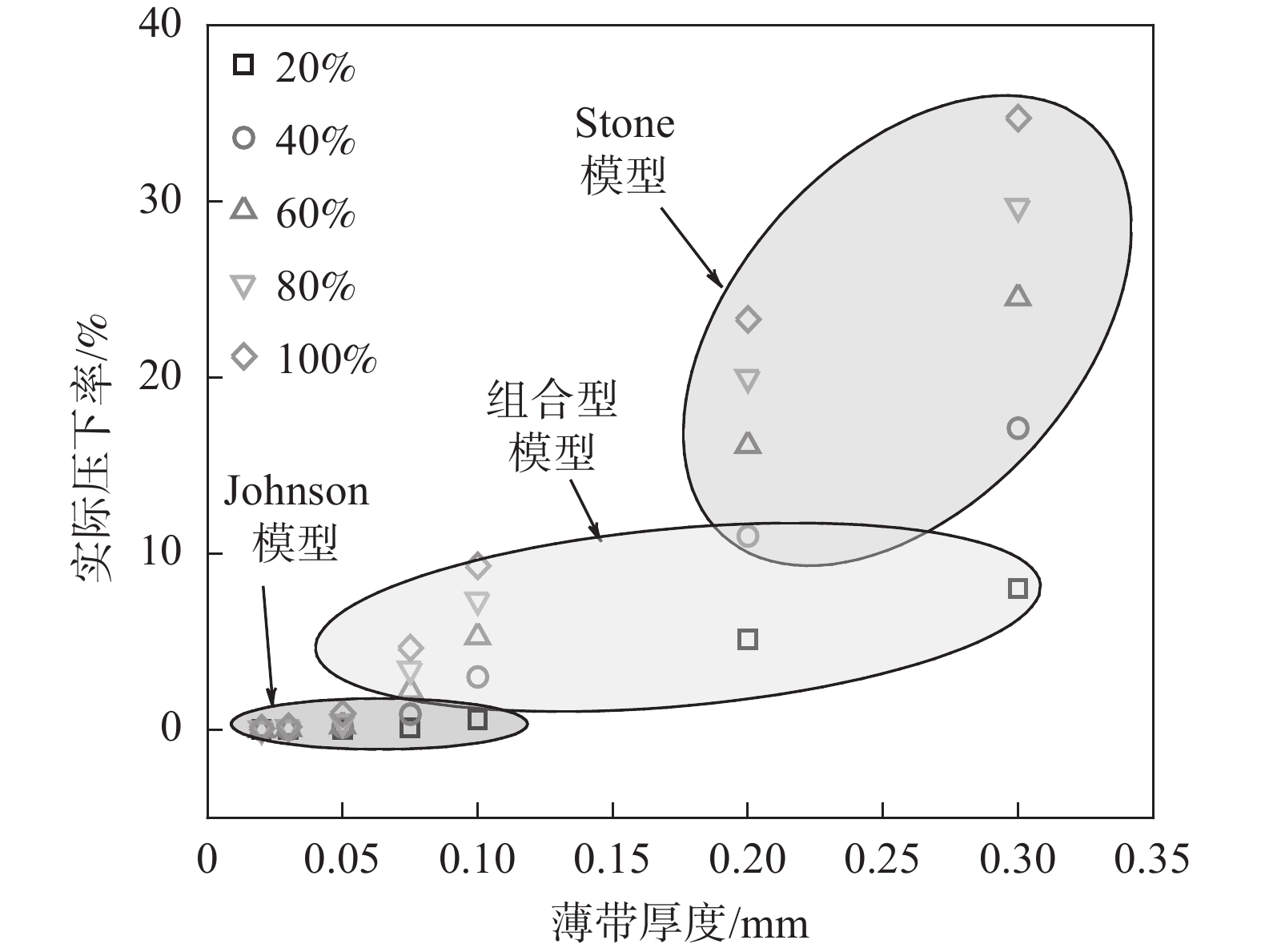
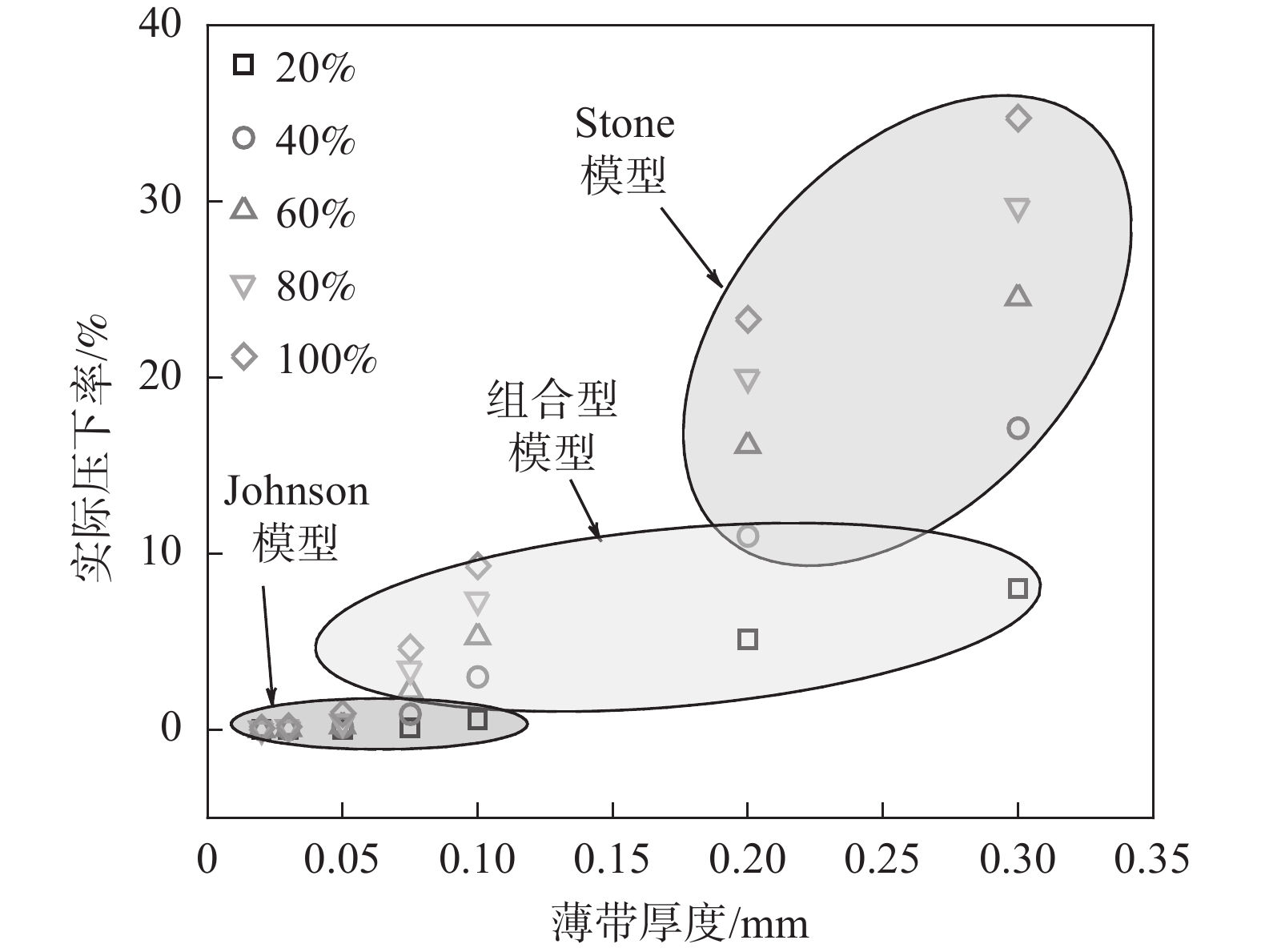
表 2 单位宽度轧制力模拟值与Johnson模型和组合模型理论值Table 2. Rolling force per unit width from FE simulation and Johnson model & combined model厚度/mm 预设压下率/% 模拟值/N 组合型理论值/N 组合型相对误差/% Stone理论值/N Stone相对误差/% 0.075 20 470.7 478.2 1.587 425.0 −9.717 40 995.0 1017.7 2.284 1082.6 8.808 60 1540.1 1554.0 0.905 2195.7 42.572 80 2105.7 2106.4 0.036 3649.7 73.326 100 2688.2 2674.3 −0.515 5629.7 109.424 0.1 20 632.5 645.0 1.975 552.2 −12.693 40 1313.7 1318.1 0.335 1284.0 −2.261 60 2036.2 2009.2 −1.326 2197.0 7.900 80 2790.9 2724.1 −2.394 4405.7 57.858 100 3572.0 3460.0 −3.136 5889.7 64.884 0.2 20 1077.3 1091.4 1.304 1068.5 −0.819 40 2231.0 2112.3 −5.318 2191.1 −1.787 60 3594.7 3273.2 −8.945 3690.6 2.666 80 5186.6 4561.5 −12.053 5203.1 0.318 100 6924.8 6011.9 −13.182 7627.7 10.151 上述结果表明Stone模型、Johnson模型和组合型模型在描述轧辊弹性压扁时有其各自的适用范围，为进一步明确各理论模型的适用性，建立了如图12所示的薄带厚度-预设压下率-实际压下率和适用模型之间的关系图。由图12可知，在模型适用范围可采用实际压下率进行划分，而与薄带厚度的关系较小: ①当实际压下率小于1%时，优先考虑全弹性假设；②当实际压下率介于1%～10%时，组合型理论模型预测精度更高；③当实际压下率大于10%时，采用Stone全滑移模型更适合。
图 12 实际压下率划分的三种模型的适用范围Figure 12. Mapping of the three models by the actual reduction ratio4. 结论
通过理论分析和数值模拟相结合的手段探究了薄带轧制变形区接触特征的变化规律，详细对比了三种接触压力模型的推导特点和适用区间，所得结论如下：
1) 轧辊弹性压扁后依次经历圆弧形、圆弧压扁增大形、非圆弧形和近直线形轮廓，而中性区的出现及其所占变形区长度比例的增加导致实际压下率快减和变形区形状系数快增。
2) 对变形区接触轮廓、界面摩擦条件和轧件弹塑性状态等认识和处理方式的不同，导致Stone模型、Johnson模型和组合型模型成立的先决条件、计算精度和适用范围存在显著差异。
3) 采用道次实际压下率可对三种理论模型的适用范围进行更准确的划分，Stone模型、组合型模型和Johnson模型分别适用于道次压下率大于10%、介于1%～10%和小于1%的轧制工况。
-
图 1 变形区微元体的受力示意
Figure 1. Schematic diagram of applied force in the deformation zone microelement
图 2 Stone模型变形区受力及接触压力分布示意
Figure 2. Schematic diagram of force and contact pressure distribution in the deformation under Stone model
图 3 Johnson模型变形区受力及接触压力分布示意
Figure 3. Schematic diagram of force and contact pressure distribution in the deformation zone under Johnson model
图 4 组合型模型变形区受力及接触压力分布示意
Figure 4. Schematic diagram of the force and contact pressure distribution in the deformation zone under the combined model
图 6 不同厚度薄带的变形区接触轮廓随压下率的变化
(a) 0.3 mm；(b) 0.2 mm；(c) 0.1 mm；(d) 0.075 mm；(e) 0.05 mm；(f) 0.03 mm
Figure 6. The contact profile of the deformation zone under different thicknesses thin strips with reduction ratio
图 7 变形区接触特征随薄带厚度的变化规律
(a) 预设压下率40%；(b) 预设压下率100%
Figure 7. The variation of the contact characteristics in deformation zone with thin strip thickness
图 8 不同厚度薄带的变形区接触压力
(a) 0.3 mm； (b) 0.2 mm；(c) 0.1 mm；(d) 0.075 mm；(e) 0.05 mm；(f) 0.03 mm
Figure 8. The contact pressure of the deformation zone under different thicknesses thin strips
图 9 接触弧长的模拟值与Hitchcock和Johnson理论值对比
(a) Hitchcock理论值；(b) Johnson理论值
Figure 9. Comparison of the contact arc length from FE simulation and Hitchcock & Johnson models
图 10 入口塑性区临界点的模拟值与组合模型理论值对比
(a) xB ；(b) xC
Figure 10. Comparison of critical point of the plastic zone at the inlet from FE simulation and combined model
图 11 接触压力模拟值与三种模型理论值对比
(a) 0.2 mm；(b) 0.1 mm；(c) 0.075 mm
Figure 11. Comparison of contact pressures from FE and three models
图 12 实际压下率划分的三种模型的适用范围
Figure 12. Mapping of the three models by the actual reduction ratio
表 1 薄带轧制工艺参数
Table 1. Thin strip rolling process parameters
薄带初始厚度h0 /mm 预设压下率y/% 0.3、0.2、0.1、0.075、0.05、0.03、0.02 20、40、60、80、100 
下载: 导出CSV
表 2 单位宽度轧制力模拟值与Johnson模型和组合模型理论值
Table 2. Rolling force per unit width from FE simulation and Johnson model & combined model
厚度/mm 预设压下率/% 模拟值/N 组合型理论值/N 组合型相对误差/% Stone理论值/N Stone相对误差/% 0.075 20 470.7 478.2 1.587 425.0 −9.717 40 995.0 1017.7 2.284 1082.6 8.808 60 1540.1 1554.0 0.905 2195.7 42.572 80 2105.7 2106.4 0.036 3649.7 73.326 100 2688.2 2674.3 −0.515 5629.7 109.424 0.1 20 632.5 645.0 1.975 552.2 −12.693 40 1313.7 1318.1 0.335 1284.0 −2.261 60 2036.2 2009.2 −1.326 2197.0 7.900 80 2790.9 2724.1 −2.394 4405.7 57.858 100 3572.0 3460.0 −3.136 5889.7 64.884 0.2 20 1077.3 1091.4 1.304 1068.5 −0.819 40 2231.0 2112.3 −5.318 2191.1 −1.787 60 3594.7 3273.2 −8.945 3690.6 2.666 80 5186.6 4561.5 −12.053 5203.1 0.318 100 6924.8 6011.9 −13.182 7627.7 10.151
下载: 导出CSV
-
[1] Mishra M K, Dubey V, Mishra P M, et al. MEMS technology: A review[J]. Journal of Engineering Research and Reports, 2019,4(1):1-24. [2] Fu M, Wang J, Korsunsky A M. A review of geometrical and microstructural size effects in micro-scale deformation processing of metallic alloy components[J]. International Journal of Machine Tools & Manufacture, 2016,109:94-125. [3] Xiao Hong, Ren Zhongkai, Liu Xiao, et al. Experiment and finite element simulation of roll flattening in deformation zone for ultra-thin strip rolling[J]. Iron and Steel, 2017,52(1):38-42. (肖宏, 任忠凯, 刘晓, 等. 极薄带轧制变形区轧辊压扁试验与有限元模拟[J]. 钢铁, 2017,52(1):38-42.Xiao Hong, Ren Zhongkai, Liu Xiao, et al. Experiment and finite element simulation of roll flattening in deformation zone for ultra-thin strip rolling[J]. Iron and Steel, 2017, 52（1）: 38-42. [4] Liu Yaxing, Gu Qing, Zhang Wenjun, et al. Improved model for calculating rolling load of ultra-high strength steel in cold rolling process[J]. Iron and Steel, 2021,56(10):108. (刘亚星, 顾清, 张文军, 等. 超高强钢冷轧过程轧制力计算的改进模型[J]. 钢铁, 2021,56(10):108.Liu Yaxing, Gu Qing, Zhang Wenjun, et al. Improved model for calculating rolling load of ultra-high strength steel in cold rolling process[J]. Iron and Steel, 2021, 56（10）: 108. [5] Karman T V. On the theory of rolling[J]. ZAMMZeitschrift fur Angewandte Mathematik und Mechanik, 1925,5:139-141. doi: 10.1002/zamm.19250050213 [6] Kuhn H A, Weinstein A S. Lateral distribution of pressure in thin strip rolling[J]. Journal of Engineering for Industry, 1970,5:453-459. [7] Kuhn H A, Weinstein A S. The minimum gauge problem in thin strip rolling[J]. Journal of Engineering for Industry, 1971,7:331-340. [8] Hitchcock J H. Roll neck bearings[R]. Report of ASME Special Research Committee. ASME, 1935: 33-41. [9] Stone M D. Rolling of thin strip part II[J]. Iron and Steel Engineer, 1956,33(12):55-76. [10] Wu Shoumin. Research of smallest permissive-rolling thickness during strip rolling[J]. China Metallurgy, 2007,17(3):10-12. (吴首民. 极薄带钢轧制过程中最小可轧厚度的研究[J]. 中国冶金, 2007,17(3):10-12. doi: 10.3969/j.issn.1006-9356.2007.03.003Wu Shoumin. Research of smallest permissive-rolling thickness during strip rolling[J]. China Metallurgy, 2007, 17（3）: 10-12. doi: 10.3969/j.issn.1006-9356.2007.03.003 [11] Tateno J, Hiruta T, Katsura S, et al. Experimental analysis of thickness reduction limits in ultra-thin stainless steel foil rolling[J]. ISIJ International, 2011,51(5):788-792. doi: 10.2355/isijinternational.51.788 [12] Liu Xiao, Fu Lun, Lu Yuefeng, et al. Theory and numerical simulation of minimum rolling thickness for thin strip rolling[J]. Iron and Steel, 2021,56(11):87-95. (刘晓, 付伦, 芦跃峰, 等. 薄带材轧制的最小可轧厚度理论及数值模拟[J]. 钢铁, 2021,56(11):87-95.Liu Xiao, Fu Lun, Lu Yuefeng, et al. Theory and numerical simulation of minimum rolling thickness for thin strip rolling[J]. Iron and Steel, 2021, 56（11）: 87-95. [13] Orowan E, Ing Dr. The calculation of roll pressure in hot and cold flat rolling[J]. Proceedings Institute of Mechanical Engineering, 1943,150(4):140-167. [14] Ford H, Ellis F, Bland D R. Cold rolling with strip tension[J]. Journal of the Iron and Steel Institute, 1951,168(1):57-72. [15] Ford H, Alexander J M. Simplified hot rolling calculations[J]. Institute Metals, 1959,88(6):193-197. [16] Bentall R H, Johnson K L. An elastic strip in plane rolling contact[J]. International Journal of Mechanical Science, 1968,10(8):637-663. doi: 10.1016/0020-7403(68)90070-2 [17] Johnson K L, Bentall R H. The onset of yield in the cold rolling of thin strip[J]. Journal of the Mechanics and Physics of Solids, 1969,17(4):253-264. doi: 10.1016/0022-5096(69)90015-5 [18] Fleck N A, Johnson K L. Towards a new theory of cold rolling thin foil[J]. International Journal of Mechanical Sciences, 1987,29(7):507-524. doi: 10.1016/0020-7403(87)90012-9 [19] Fleck N A, Johnson K L, Mear M E, et al. Cold rolling of foil[J]. Proceedings of The Institution of Mechanical Engineers Part B-Journal of Engineering Manufacture, 1992, 206(2): 119-131. [20] Xiao Hong, Liu Xiao. Theory and numerical simulation of gauge suitable to roll in ultra-thin strip rolling[J]. Iron and Steel, 2019,54(6):48-55. (肖宏, 刘晓. 极薄箔带轧制的适轧厚度理论及数值模拟[J]. 钢铁, 2019,54(6):48-55.Xiao Hong, Liu Xiao. Theory and numerical simulation of gauge suitable to roll in ultra-thin strip rolling[J]. Iron and Steel, 2019, 54（6）: 48-55. [21] Xiao Hong, Ren Zhongkai, Liu Xiao. New mechanism describing the limiting producible thickness in ultra-thin strip rolling[J]. International Journal of Mechanical Sciences, 2017,133:788-793. doi: 10.1016/j.ijmecsci.2017.09.046 [22] Liu Xiao, Xiao Hong. Theoretical and experimental study on the producible rolling thickness in ultra-thin strip rolling[J]. Journal of Materials Processing Technology, 2020,278:116537. doi: 10.1016/j.jmatprotec.2019.116537 [23] Li Wei, Li Songsong, Yu Hui. Theoretical study on the limit rollable thickness of thin strip based upon rolling force[J/OL]. Engineering Mechanics,1-9[2024-12-02]. http://kns.cnki.net/kcms/detail/11.2595.o3.20230928.1640.014.html. (李伟, 李松松, 于辉. 基于轧制力判定的薄带材极限可轧厚度理论研究[J/OL]. 工程力学, 1-9[2024-12-02]. http://kns.cnki.net/kcms/detail/11.2595.o3.20230928.1640.014.html.Li Wei, Li Songsong, Yu Hui. Theoretical study on the limit rollable thickness of thin strip based upon rolling force[J/OL]. Engineering Mechanics,1-9[2024-12-02]. http://kns.cnki.net/kcms/detail/11.2595.o3.20230928.1640.014.html. [24] Li W, Li S S, Yu H. Research on the anisotropy of plastic behavior and deformation mechanism of textured pure titanium[J]. Materials Characterization, 2022, 194: 112483. [25] Li Wei, Yu Hui, Li Songsong, et al. Yield behavior of cold-rolled pure titanium thin strip based on anisotropy[J]. Rare Metal Materials and Engineering, 2023,52(9):3213-3220. (李伟, 于辉, 李松松, 等. 基于各向异性冷轧纯钛薄带的屈服行为研究[J]. 稀有金属材料与工程, 2023,52(9):3213-3220. doi: 10.12442/j.issn.1002-185X.20220739Li Wei, Yu Hui, Li Songsong, et al. Yield behavior of cold-rolled pure titanium thin strip based on anisotropy[J]. Rare Metal Materials and Engineering, 2023, 52（9）: 3213-3220. doi: 10.12442/j.issn.1002-185X.20220739 -
下载:
点击查看大图
计量
- 文章访问数: 86
- HTML全文浏览量: 46
- PDF下载量: 9
- 被引次数: 0
