Numerical simulation of fluidized chlorination velocity of high titanium slag
-
摘要: 基于高钛渣和氯气物性参数，采用经典初始流化速度公式计算了高钛渣沸腾氯化的初始流化速度，并结合欧拉双流体模型建立了高钛渣沸腾氯化气固两相流的数学模型并开展数值计算，最后以数值模拟结果为依据对高钛渣沸腾氯化表观操作气速进行了预测。研究结果表明：以欧拉双流体模型结合Grace公式得到初始流化速度能够准确模拟出高钛渣氯化过程的气固两相流特征；依据沸腾氯化床层中高钛渣颗粒体积分数、床层截面速度和压力分布规律，确定高钛渣沸腾氯化的最佳表观操作气速为Grace计算公式得到的初始流化速度值的1.5倍。Abstract: Based on the physical parameters of high titanium slag and chlorine gas, the initial fluidization velocity of fluidized chlorination of high titanium slag was calculated by using the classical initial fluidization velocity formula. And the mathematical model of gas-solid two-phase flow of fluidized chlorination of high titanium slag was established by combining Euler two-fluid model. Finally, based on the numerical simulation results, the superficial gas velocity of fluidized chlorination of high titanium slag was predicted. The results show that the initial fluidization velocity obtained by Euler two-fluid model combined with Grace formula can accurately simulate the gas-solid two-phase flow characteristics of high titanium slag chlorination process. According to the volume fraction of high titanium slag particles in the fluidized chlorination bed, the velocity and pressure distribution of the cross section of the bed, the optimal superficial gas velocity for the fluidized chlorination of high titanium slag was determined to be 1.5 times the initial fluidization velocity obtained by Grace’s calculation formula.
-
0. 引言
四氯化钛是海绵钛和钛合金制备的重要中间原料，生产工艺包括熔盐氯化、沸腾氯化和竖炉氯化等[1]；沸腾氯化法是以高钛渣为原料，采用氯气作为氯化剂和流化介质，高钛渣和氯气在沸腾氯化炉内逆向交互运动并发生氯化反应。因此，沸腾氯化具有良好的传质和传热效果、操作简单，易于连续生产、原料和设备利用率较高等诸多优势[2−3]，成为四氯化钛制备的重要研究方向之一。
高钛渣沸腾氯化制备四氯化钛虽具有明显的工艺优势，但原料要求较高，已有研究表明：攀枝花高钛渣经磁选除铁后CaO+MgO的含量高达6.56% [4]，在氯化过程中优先与氯气反应生成低熔点的CaCl2和MgCl2，在氯化温度下呈熔融状态易与高钛渣发生粘连团聚，导致床层出现粘结失流，不宜作为沸腾氯化的原料[5]。云南高钛渣（下文简称高钛渣）中CaO+MgO的含量约为2.5 %，相关研究者[6-7]考虑在高钛渣中合理的增加配炭量，能够有效解决CaCl2和MgCl2带来的粘结失流问题。但沸腾氯化表观操作气速直接影响高钛渣和氯气两相流的基本特征、氯化反应过程中的传热和传质效率，以及杂质的去除效率，因此，研究沸腾氯化的表观操作气速对掌握沸腾氯化炉内钛渣和氯气的气固两相流体动力学，对优化沸腾氯化工艺和参数、提高氯化效率具有重要意义。Kang等人[8]以高钛渣为原料开展了沸腾氯化的实验研究，研究结果发现：沸腾氯化过程中氯气通入速率对沸腾氯化的转化率和杂质Fe、Mn以及Mg的去除效果存在正相关的关系。陈一凡[9]采用热力学计算软件计算了沸腾氯化过程中氯化反应的热力学和化学平衡，发现当炉内氯气过量，能保证反应物充分被氯化；田键[10]结合沸腾氯化工艺，对影响沸腾氯化反应的因素进行了研究，发现氯气的表观操作气速和浓度与氯化率成正态分布关系；现有的研究仅是以试验的方法探索了表观操作气速与杂质去除率、炉内氯气分压以及提高氯化效率之间的关系；到目前为止，还未见采用初始流化速度经验计算公式为依据来确定钛渣沸腾氯化表观操作气速的研究。
基于此，笔者为了确定高钛渣沸腾氯化表观操作气速的选择方法，探究氯气的表观操作气速对高钛渣和氯气两相流的作用规律，以欧拉双流体模型为基础结合初始流化速度计算的经验公式建立了高钛渣沸腾氯化气固两相流数值模拟的数学模型；以高钛渣和氯气的基本物性参数结合准二维的流态化模型开展了高钛渣沸腾氯化气固两相流的数值计算，以气固两相流特征为基础，提出高钛渣沸腾氯化过程中基于传统经验公式的氯气表观操作气速修正式，为高钛渣沸腾氯化过程中氯气表观操作气速的选择提供参考，也能为实际生产过程中判断高钛渣沸腾氯化过程中气固两相流的转变提供指导。
1. 高钛渣初始流化速度计算的经验公式
氯气表观操作气速是沸腾氯化炉内高钛渣的流动形态的转变的重要影响因素。其转变规律符合两相流流域的基本转变规律：当氯气表观操作气速较小时，高钛渣床层表现为固定床；当氯气表观操作气速增加，床内高钛渣颗粒之间发生相互分离，床层孔隙率增大，氯气从高钛渣空隙中穿过床层，导致床层发生均匀膨胀，床层具备初步的流动性，此时的床层称为膨胀床；随着氯气表观操作速度进一步增大，氯气在通过床层使床层界面的压降大致与床层截面上的高钛渣颗粒重力相等，床内的高钛渣开始流化，此时氯气的表观操作气速称为初始流化速度，床层被称为初始流化床；随着氯气的表观操作气速大于初始流化速度，高钛渣的床层表现出现明显非均匀性，床层内部会出现氯气富集的气泡相和氯气与高钛渣混合产生的密集相（乳相），此时床层被称为鼓泡床；当氯气的表观操作气速进一步增加，高速氯气进入到床层使高钛渣发生剧烈的搅拌，床层内部非均匀性加剧，床层中出现沸腾现象，但是床层沸腾现象发生在一定范围内，氯气与高钛渣仍存在明显的界面，此时床层被称为沸腾床。
根据气固两相流流域转变的基本特征可知，高钛渣沸腾氯化的表观操作气速大于初始流化速度。因此，本研究基于颗粒两相流中预测初始流化速度的经验公式：Wen-Yu方程、Grace方程和Ergun方程为基础，开展高钛渣沸腾氯化初始流化速度计算，以初始流化速度计算结果为基础结合数值计算，开展高钛渣沸腾氯化表观操作气速预测公式修正，旨在为高钛渣沸腾氯化过程中表观操作气速的选择提供理论支持。
当床层进入初始流化状态，氯气对高钛渣颗粒产生向上的曳力与高钛渣颗粒的重力相等，忽略氯气与高钛渣和壁面产生的摩擦力，根据静力学平衡特征可知：
$$ \Delta PA\mathrm{_c}=W_{\mathrm{b}}=H\mathrm{_{mf}}A\mathrm{_c}\left\{\left(1-\varepsilon_{\mathrm{mf}}\right)\rho_{\mathrm{p}}+\varepsilon_{\mathrm{mf}}\rho_{\mathrm{f}}\right\}g $$ (1) 式中,ΔP为床层静压，Pa；Ac为床层截面积，m2；Wb为床层截面重力，N；ɛmf为初始流化下床层的空隙率，无量纲；ρp为固体颗粒的密度，kg/m3；ρf为气体的密度，kg/m3；g取9.8 m/s2。
将式(1)与Ergun公式[11]联立后可以得出初始流化速度$ u_{\mathrm{mf}} $的二次方程：
$$ \begin{split} & \frac{1.75}{\phi_{\mathrm{s}}\varepsilon_{\mathrm{mf}}^3}\left(\frac{d_{\mathrm{p}}u_{\mathrm{mf}}\rho_{\mathrm{f}}}{\mu}\right)^2+\frac{150\left(1-\varepsilon_{\mathrm{mf}}\right)}{\phi\mathrm{_s^2}\varepsilon_{\mathrm{mf}}^3} \\ & \left(\frac{d_{\mathrm{p}}u_{\mathrm{mf}}\rho_{\mathrm{f}}}{\mu}\right)=\frac{d_{\mathrm{p}}^3\rho\mathrm{_f}\left(\rho\mathrm{_p}-\rho\mathrm{_f}\right)g}{\mu^2}\end{split} $$ (2) 式中,dp为颗粒的直径，m；ϕs为颗粒的球形度，无量纲；μ为流化气体的黏度，Pa·s；umf为初始流化速度，m/s。
针对式(2)，Wen和Yu[12]的研究结果发现：对各种不同颗粒的气固两相流系统均存在如下近似的关系：
$$ \frac{1}{\phi\mathrm{_s}\varepsilon_{\mathrm{mf}}^3}\approx14 $$ (3) $$ \frac{1-\varepsilon\mathrm{_{mf}}}{\phi_{\mathrm{s}}^2\varepsilon_{\mathrm{mf}}^3}\approx11 $$ (4) 将式(3)和式(4)带入式(2)中得：
$$ \frac{d_{\mathrm{p}}u_{\mathrm{mf}}\rho_{\mathrm{f}}}{\mu}=\left[C_1^2+C_2\frac{d_{\mathrm{p}}^3\rho_{\mathrm{f}}\left(\rho_{\mathrm{p}}-\rho_{\mathrm{f}}\right)g}{\mu^2}\right]^{\tfrac{1}{2}}-C_1 $$ (5) 其中高钛渣颗粒氯化过程中初始流化速度umf的关系与不同粒径高钛渣沸腾氯化过程中的惯性力和粘性力的无因次关系如式(6)所示：
$$ Re_{\mathrm{mf}}=\frac{d\mathrm{_p}u\mathrm{_{mf}}\rho\mathrm{_f}}{\mu} $$ (6) 式中, Remf为初始流化速度下颗粒的雷诺数，无量纲。
Wen-Yu等人依据颗粒流动过程流动形态存在层流湍流等特征，提出了雷诺数范围属于0.001 ～
4000 ，颗粒粒径为0.02 ～ 19.7 mm，床层孔隙率属于0.136 ～ 1的计算不同颗粒雷诺数的初始流化速度表达式如下[12]。对于$ Re\mathrm{_{mf}} < 20 $，气固两相流间忽略颗粒的惯性力，则初始流化速度的表达式为：
$$ umf = \frac{{\mathop d\nolimits_p^2 \left( {\mathop \rho \nolimits_p \mathop { - \rho }\nolimits_g } \right)g}}{{1\;650\mu }} $$ (7) 对于$ Re_{\mathrm{mf}} > 1\; 000 $，气固两相流间忽略颗粒的粘性力，则初始流化速度的表达式为：
$$ u_{mf}^{^2} = \frac{{\mathop d\nolimits_p \left( {\mathop \rho \nolimits_p - \mathop \rho \nolimits_g } \right)g}}{{24.5\mathop \rho \nolimits_g }} $$ (8) Grace[13]在以气固两相流中颗粒运动特征和气固两相流交互机制为依据，提出了全颗粒雷诺数范围的初始流化速度计算的经验公式：
$$ \frac{{\mathop d\nolimits_p {u_{{\text{mf}}}}\mathop \rho \nolimits_g }}{\mu } = \mathop {\left[ {\mathop C\nolimits_1^2 + \mathop C\nolimits_2 \frac{{\mathop d\nolimits_p^3 \mathop \rho \nolimits_g \left( {\mathop \rho \nolimits_s - \mathop \rho \nolimits_g } \right)g}}{{\mathop \mu \nolimits^2 }}} \right]}\nolimits^{\tfrac{1}{2}} - \mathop C\nolimits_1 $$ (9) 其中，C1 = 27.2和C2 =
0.0408 。Ergun[11]在进行气固两相流流动特征预测时，进一步考虑了流化介质的粒径、密度，粘度等容易测量的物性参数，对初始流化速度公式(9)进行了进一步修正，得到了全雷诺数范围下的初始流化速度计算公式中的常数取值为：C1 = 33.7，C2 =
0.0408 。2. 高钛渣沸腾氯化数值模拟的基本模型
欧拉双流体模型是描述气固两相流的一个基本模型，该模型主要是将固体颗粒认为是拟流体，分别采用气相和拟流体相的连续性方程和动量方程来描述气固两相流过程中相关运动参数，最后采用气固相间的相互作用力来耦合封闭方程。
2.1 欧拉双流体模型
本次采用欧拉双流体模型作为高钛渣沸腾氯化气固两相流数值模拟的数学模型，其中在气固两相流中将高钛渣相作为拟流体相，认为高钛渣相和氯气相在沸腾氯化过程中共同存在且相互渗透的连续介质模型[14]，主要包括高钛渣相和氯气相的连续性方程和动量守恒方程。
连续性方程：
氯气相：
$$ \frac{\partial(\varepsilon\mathrm{_g}\rho_{\mathrm{g}})}{\partial t}+\nabla\cdot(\varepsilon\mathrm{_g}\rho_{\mathrm{g}}\vec{u}_{\mathrm{g}})=0 $$ (10) 高钛渣相：
$$ \frac{\partial((1-\varepsilon g)\rho\mathrm{_p})}{\partial t}+\nabla\cdot((1-\varepsilon g)\rho_{\mathrm{p}}\vec{u}_{\mathrm{p}})=0 $$ (11) 动量守恒方程：
氯气相：
$$ \begin{split} & \frac{\partial(\varepsilon\mathrm{_g}\rho\mathrm{_g}u_{\mathrm{g}})}{\partial t}+\nabla\cdot(\varepsilon_{\mathrm{g}}\rho_{\mathrm{g}}\vec{u}_{\mathrm{g}}\vec{u}_{\mathrm{g}})= \\ & \nabla\cdot(\varepsilon_{\mathrm{g}}\tau_{\mathrm{g}})+\varepsilon\mathrm{_g}\rho\mathrm{_g}g-\varepsilon_{\mathrm{g}}\nabla P-\beta(\vec{u}_{\mathrm{g}}-\vec{u}_{\mathrm{p}})\end{split} $$ (12) 高钛渣相：
$$ \begin{split} & \frac{\partial\left(\left(1-\varepsilon\mathrm{_g}\right)\rho_{\mathrm{p}}u_{\mathrm{p}}\right)}{\partial t}+\nabla\cdot\left(\left(1-\varepsilon\mathrm{_g}\right)\rho_{\mathrm{p}}\vec{u}_{\mathrm{p}}\vec{u}_{\mathrm{p}}\right)= \\ & \nabla\cdot\left(1-\varepsilon_{\mathrm{g}}\right)\tau_{\mathrm{p}}+\left(1-\varepsilon_{\mathrm{g}}\right)\rho_{\mathrm{p}}g-\left(1-\varepsilon_{\mathrm{g}}\right)\nabla P+ \\ & \beta\left(\vec{u}_{\mathrm{g}}-\vec{u}_{\mathrm{p}}\right)+\nabla\rho_{\mathrm{p}}\end{split} $$ (13) 式中，ε为床层空隙率，无量纲；ρ为密度，kg/m3；u为速度，m/s；τ为时间，s；P为压强，Pa；β为气固相间曳力，N；下标p和g分别表示高钛渣相和氯气相。
2.2 气固两相间的曳力模型
上述欧拉双流体模型方程中，氯气相与高钛渣的运动方程和守恒方程是独立存在的，但在数值计算过程中，为了表达氯气相和高钛渣相的相互作用效果，封闭求解数学模型，在此引入氯气相和高钛渣相之间相互存在的曳力计算模型，在描述气固两相运动中，通常采用Gidaspow曳力模型。
Gidaspow曳力模型[15]涉及的主要方程：
$$ \begin{split} \beta = 150\frac{{{{\left( {1 - \varepsilon g} \right)}^{^2}}{{\vec u}_g}}}{{\varepsilon g{{\left( {{d_p}{\varphi _p}} \right)}^{^2}}}} + 1.75\frac{{{\rho _g}\left( {1 - \varepsilon g} \right)\left| {{{\vec u}_g} - \left. {{{\vec u}_p}} \right|} \right.}}{{{d_p}{\varphi _p}}}\\ \left( {\varepsilon g < 0.8} \right), \end{split} $$ (14) $$ \beta = \frac{3}{4}{C_D}\frac{{{\rho _g}\left( {1 - {\varepsilon _g}} \right)\left| {{{\vec u}_g} - \left. {{{\vec u}_p}} \right|} \right.}}{{{d_p}{\varphi _p}}}{\varepsilon _g} - 2.65 \left( {{\varepsilon _g} > 0.8} \right), $$ (15) 其中，曳力系数CD表示为
$$ C\mathrm{_D}=\left\{\begin{array}{*{20}{l}}\dfrac{24}{Re_{\mathrm{p}}}\left[1+0.15\left(\varepsilon gRe_{\mathrm{p}}\right)^{0.675}\right] & \left(Re\mathrm{_P} < 1\; 000\right), \\ 0.44 & \left(Re\mathrm{_p}\geqslant1\; 000\right),\end{array}\right. $$ (16) 式中，φ为高钛渣球形度，无量纲；μ为黏度，Pa·s；d为颗粒粒径，m；β为气固界面曳力系数；$\tau $为应力张量；CD为曳力系数；Re为雷诺数；g取9.8 m/s2；下标p和g分别表示高钛渣相和氯气相。
2.3 几何模型和边界条件
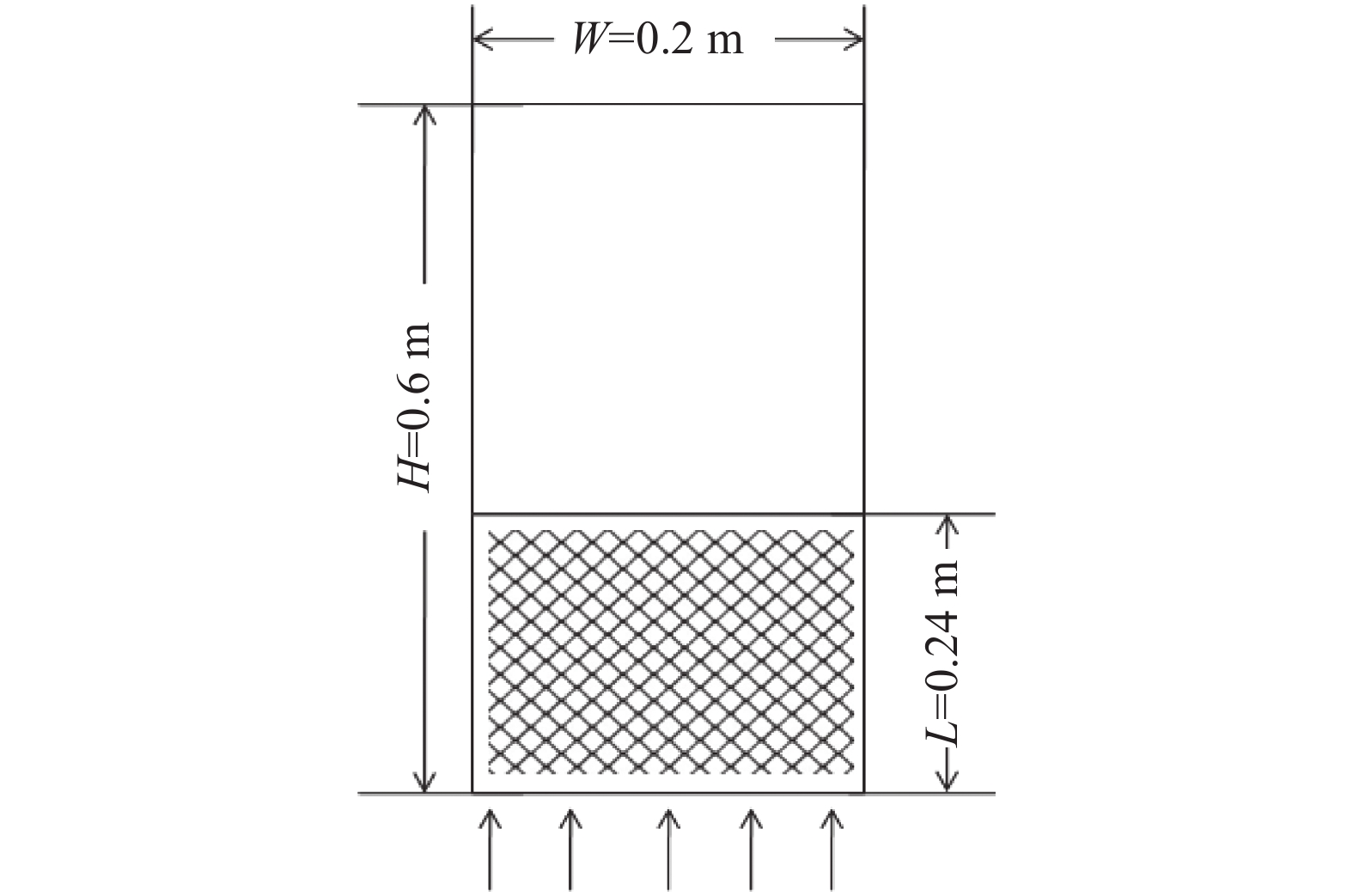
本次数值计算以B类颗粒[16](粒度：100 ～ 600 μm，密度：1 400 ～ 4 000 kg/m3)的高钛渣为研究对象，考虑单一粒径范围的高钛渣在氯气作用下沸腾氯化的气固两相流特征。高钛渣沸腾氯化的几何模型的建立、网格的划分和边界条件设定在Gambit软件中完成。为了方便观察高钛渣沸腾氯化过程汇总气固两相流中气泡相的形态，此次研究采用准二维分布板流化床模型进行求解，具体几何模型如图1所示。
数学模型求解采用 Fluent 6.3.26计算流体力学软件包进行，即综合式(1)～(13)的求解，其中欧拉双流体模型和Gidaspow曳力模型为Fluent软件自带模型。整个模拟采用非稳态求解，具体求解方法为Simple算法，粘性模型选择RNG k-ε。在壁面处，气-固两相流采用无滑移边界条件，体积分数差分格式选择QUICK格式。计算时，连续性方程X和Y两个方向上动量方程的残差精度为：
0.0001 。各种数值模拟参数如表1所示。表 1 边界条件和模拟参数Table 1. Boundary conditions and simulation model parameters钛渣密度/(kg·m−3) 钛渣直径/m 初始体积分数 氯气密度/(kg·m−3) 初始静床高/m 床层空隙率 曳力模型 3810 5×10−4 0.7 2.95 0.24 0.61 Gidaspow 湍流模型 求解算法 内摩擦角/(°) 时间步长 时间步数 收敛标准 网格数目 RNG-k-ε Simple 30 10−4 30 000 0.0001 10 000 以表1中所示关于高钛渣和氯气的参数为基础，结合初始流化速度计算公式(6)～(9)，分别以不同经验计算公式计算了高钛渣沸腾氯化过程初始流化速度，计算结果如表2所示。然后以初始流化速度为依据，进行高钛渣沸腾氯化过程数值模拟计算。
表 2 不同经验公式计算的高钛渣初始流化速度Table 2. Initial fluidization velocity of high titanium slag calculated by different empirical formulasm/s 经验计算公式 Grace公式 Wen-Yu 公式 Ergun公式 计算值 0.425 0.319 0.288 根据表2数据可知，不同初始流化速度的经验计算公式计算结果存在明显的差异，因此，为了进一步探究初始流化速度经验计算公式对高钛渣沸腾氯化初始流化状态气固两相流的流体动力学特征的准确性，笔者首先基于表2的经验公式计算值为依据，开展钛渣沸腾氯化气固两相流数值计算；对比B类颗粒流化特征，选定符合高钛渣的最佳初始流化速度经验公式，为进一步修正得到沸腾氯化速度奠定基础。
3. 结果分析与讨论
3.1 不同初始流化速度下高钛渣沸腾氯化数值模拟结果分析
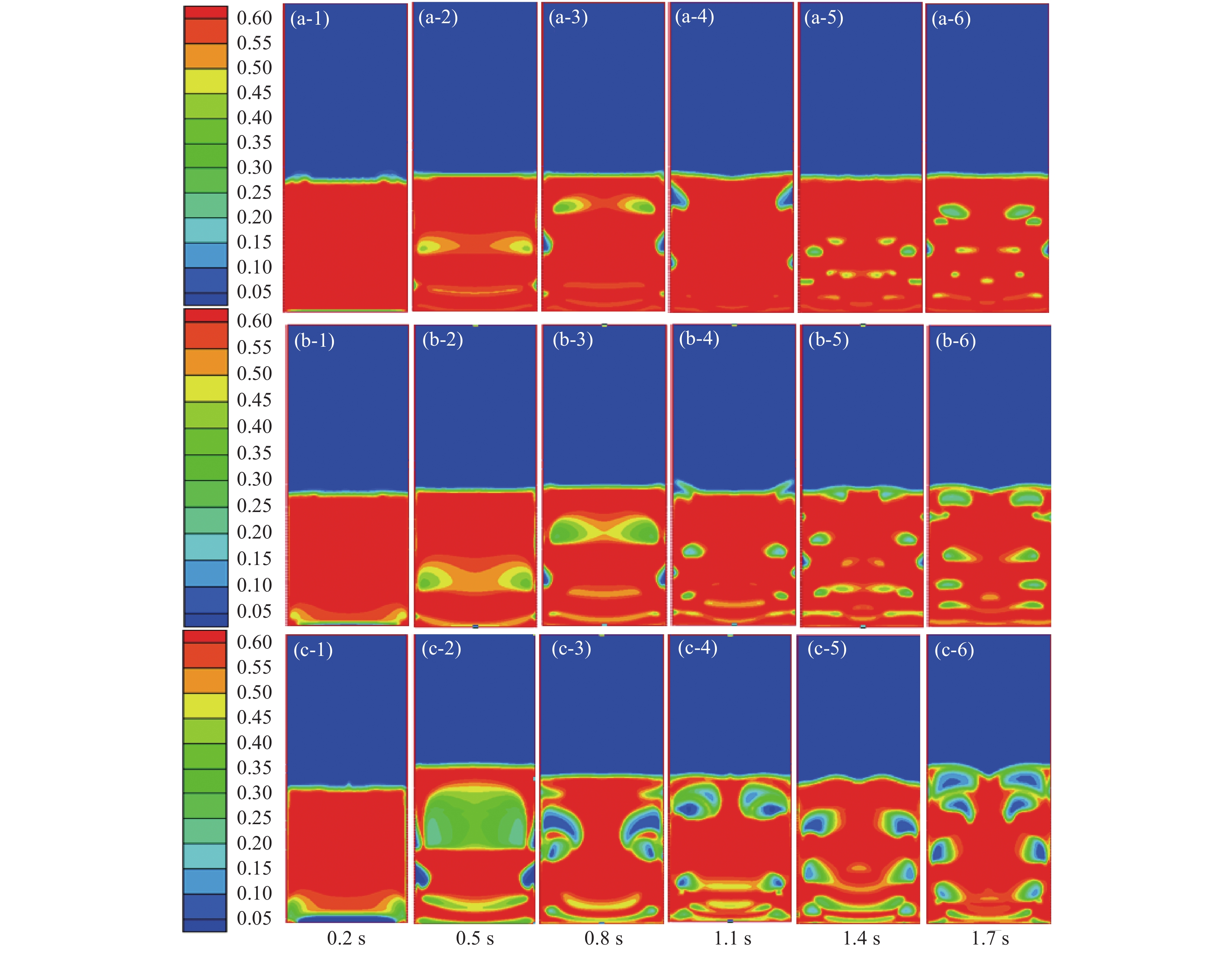
根据表1所示高钛渣的物性结合B类颗粒特征(粒度：100 ～ 600 μm，密度：1 400 ～ 4 000 kg/m3)，高钛渣颗粒满足B类颗粒特征，其流化特征为：当氯气的表观操作气速达到高钛渣颗粒的初始流化速度时，在分布板位置形成气泡。图2是不同初始流化速度经验计算得到的理论值作为表观操作气速下，数值计算得到的高钛渣沸腾氯化过程中高钛渣颗粒的云图。
图 2 不同初始流化速度下高钛渣颗粒体积分数云图（a-1）～（a-6）：初始流化速度为0.288 m/s (Ergun公式)；（b-1）～（b-6）：初始流化速度为0.319 m/s (Wen-Yu公式)；（c-1）～（c-6）：初始流化速度为0.425 m/s (Grace公式)Figure 2. Particle volume fraction of high-titanium slag under different initial fluidization velocities根据Patil等人[17]的研究结果可知：当气体的体积分数（空隙率）εg=0.85时即认为形成气泡[14]，因此，在本研究中将高钛渣体积分数小于0.15的相认为是气泡相，高钛渣颗粒的体积分数在0.15～0.61内的相认为是乳相。根据图2所示可知，当表观操作气速为0.288 m/s，流化时间为0.2 s时，床层中首先在分布板位置形成狭长的沟流现象，随着流速增加，由于壁面效应在壁面位置开始出现明显气泡，当流化时间为0.8 s时，壁面位置处的气泡在上升过程中不断长大，而中间乳相也不断上升，但此时床层中下部出现明显的横向乳相区（图2(a-3)）；随着流化的进行，中间横向乳相区受到分布板来流氯气的影响，逐渐演化为分散的乳相区（如图2(a-5)），最后乳相区不断上升、长大最后破裂。当表观操作气速为0.319 m/s时，高钛渣和氯气两相流特征与表观操作气速为0.288 m/s时基本相似，在床层底部首先出现横向沟流，随着流化时间延长，床层壁面处开始出现气泡，床层底部出现的横向乳相区，随着流化时间延长，开始演化为中间分散的乳相区；当表观操作气速为0.415 m/s时，首先在床层底部出现横向沟流区（如图2(c-1)），当流化时间延长，在床层壁面位置开始出现气泡相，底部沟流区开始演化为乳相区域，并不断向上迁移（如图2(c-2)），当留流化时间为0.8 s时，此时床层在靠近壁面位置开始形成了气泡相，随着流化时间延长，床层内部气泡相越来越多，且呈现出稳定上升、长大和破裂现象（如图2(c-6)）。
从数值模拟得到的高钛渣颗粒体积分数云图的结果可知，Grace公式计算得到初始流化速度为0.425 m/s，在表观操作气速为0.425 m/s时，高钛渣床层中出现了稳定、连续上升的气泡行为，与其他研究者采用B类颗粒进行数值计算得到的气泡规律一致[18]；而Wen-Yu公式和Ergun公式计算得到的初始流化速度的模拟结果中仅在壁面位置出现气泡，床层中基本以乳相为主；因此，结合B类颗粒流动特征，采用Grace公式计算结果能够准确模拟高钛渣沸腾氯化的鼓泡流化行为。
3.2 基于高钛渣沸腾氯化气固两相流特征预测表观操作气速
沸腾流化过程中关于“沸腾”状态的研究结果发现[19]：沸腾状态是指床层中气泡连续不断生成、上升和破裂，在这个过程中，气泡的上升对床层内部固体颗粒产生了剧烈的搅拌作用，发生强烈的气固交互现象。根据初始流化速度下高钛渣气固两相流云图研究结果发现： Grace公式计算得到的初始流化速度下，床层内部仅仅开始出现稳定的气泡行为，气泡运动速率不足以实现对床层颗粒产生明显搅拌作用，因此，为了准确模拟高钛渣沸腾氯化过程，本研究以Grace公式计算结果为基础，以1.1、1.2、1.3、1.4、1.5倍和1.6倍初始流化速度(
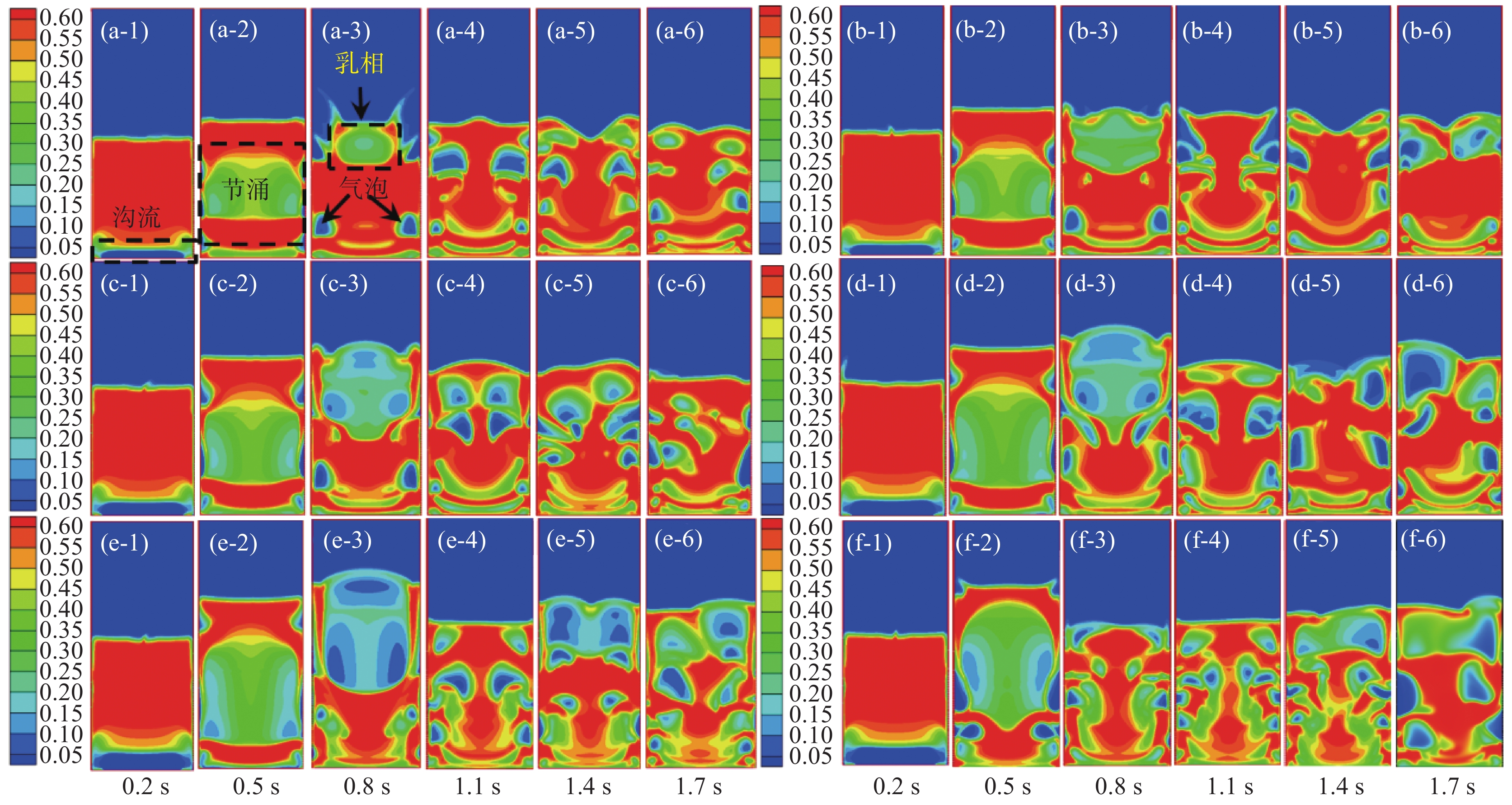
0.4675 、0.51、0.5525 、0.595、0.6375 m/s和0.68 m/s)作为氯气的表观操作气速，开展了高钛渣沸腾氯化的数值计算，计算结果如图3所示。
图 3 不同修正系数下固体颗粒体积分数云图（a-1）～（a-6）: 1.1倍初始流化速度(0.4675 m/s)；（b-1）～（b-6）: 1.2倍初始流化速度(0.51 m/s)；（c-1）～（c-6）: 1.3倍初始流化速度(0.5525 m/s)；（d-1)～（d-6）: 1.4倍初始流化速度(0.595 m/s)；（e-1）～（e-6）: 1.5倍初始流化速度(0.6375 m/s)；（f-1）～（f-6）: 1.1倍初始流化速度(0.68 m/s)Figure 3. Volume fraction of solid particles under different correction coefficients在不同修正倍数条件下，床层内部气固两相流运动特征相似，大致可以分为如下阶段：沸腾流化启动阶段、沸腾流化过渡阶段和沸腾流化阶段。沸腾流化启动阶段：在氯气通入床层开始阶段，首先会在床层底部形成一个横向沟流区域，主要由于床层初始堆积密度较大，底部氯气来流速度较快，进入床层的氯气来不及从高钛渣颗粒间穿过床层，易在床层底部聚集，形成沟流区域，如图3中所示0.2 s的云图结果；随着流化时间的延长，床层中由于氯气聚集较多，床层发生明显膨胀，但是由于膨胀区域上部的氯气与高钛渣颗粒发生动量交换，导致氯气速度比床层入口速度低而达不到高钛渣颗粒的初始流化速度，高钛渣颗粒的重力大于氯气对其的曳力，高钛渣颗粒将会下沉并与沟流区域的氯气混合形成乳相区，随着流化的进行，乳相区面积逐渐增加，将床层分割为两个固相区域，床层中出现明显的节涌现象如图3所示0.5 s的云图结果，高钛渣进入沸腾氯化的过渡阶段；随着流化时间延长，床层中部的乳相区逐渐增大和上升，此时床层上部高钛渣颗粒向两侧壁面迁移并向下运动与乳相上升形成逆向运动，最后乳相区域破裂，此时过渡阶段结束，床层进入沸腾氯化阶段。
从图3中可以发现：表观操作气速为1.1～1.5倍初始流化速度时，床层在0.8 s后进入沸腾氯化阶段；表观操作气速为1.6倍初始流化速度时，床层在0.5 s后进入沸腾流化阶段；但是从图中可以发现：当表观操作气速为1.1 ～1.4倍初始流化速度时，床层中虽然出现稳定连续的气泡现象，但是云图中红色区域(高钛渣体积分数约为0.6左右)面积较大，表现出较为聚集的现象，此时床层中颗粒团聚现象较为明显，气泡对高钛渣的搅拌并不明显，高钛渣相和气相混合并不均匀，在高温氯化过程中，高钛渣团聚区域易出现粘结失流；但是当氯气表观操作气速为1.5倍初始流化速度后，当进入沸腾氯化阶段后，如图(3e-4～e-6)和图(3f-4～f-6)所示云图中红色区域(高钛渣体积分数约为0.6左右)面积相比于其他倍数初始流化速度作为表观操作气速时获得的高钛渣颗粒云图中红色区域面积要小得多；因此，根据数值模拟结果得到的高钛渣颗粒的云图分析，可以确定在沸腾氯化时，高钛渣表观操作气速要选择大于1.5倍Grace公式计算得到的初始流化速度值。
3.3 基于床层稳定性预测高钛渣沸腾氯化表观操作气速
根据不同倍数初始流化速度计算得到高钛渣沸腾氯化高钛渣颗粒体积分数云图的分析结果发现：高钛渣沸腾氯化速度的表观操作气速应选择以Grace公式计算值的1.5倍以上，但是实际操作过程应当进一步考虑氯化过程经济性以及沸腾氯化过程中床层稳定性等问题，应该在沸腾氯化基础上合理选择表观操作气速，因此，本文在1.5倍和1.6倍初始流化速度(
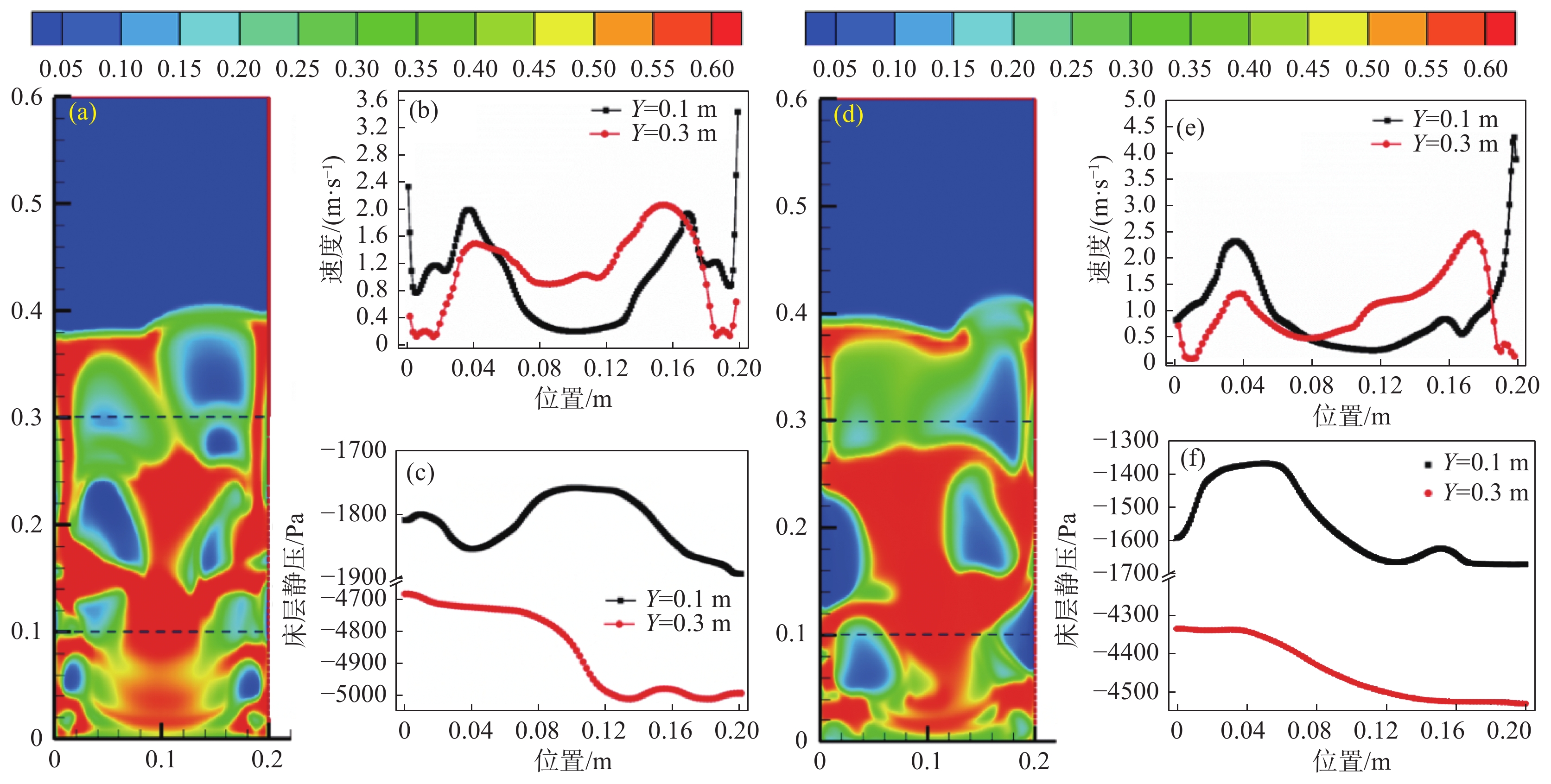
0.6375 m/s和0.68 m/s)下，以高钛渣沸腾氯化气固两相流数值模拟结果为基础，选择沸腾氯化时间为1.7 s时，分析床层截面为Y=0.1 m和Y=0.3 m处的速度分布规律和静压分布规律，结果如图4所示；以床层速度分布规律和压力分布规律的期望与方差值为依据，进一步确定高钛渣沸腾氯化的表观操作气速。
图 4 不同表观操作气速下，高钛渣体积分数和不同截面处速度和压力的关系(a)表观操作气速为0.6375 m/s，沸腾氯化时间为1.7 s时的高钛渣体积分数云图；(b)图(a)中Y=0.1 m 和Y=0.3 m处高钛渣颗粒速度；(c)图（a）中Y=0.1 m 和Y=0.3 m处床层截面静压；(d) 表观操作气速为0.68 m/s，沸腾氯化时间为1.7 s时的高钛渣体积分数云图；(e)图(d)中Y=0.1 m 和Y=0.3 m处高钛渣颗粒速度；(f) 图(d)中Y=0.1 m 和Y=0.3 m处床层截面静压Figure 4. Relationship between the volume fraction of high titanium slag and the velocity and pressure at different sections under different apparent operating gas velocities从图4可以发现，床层截面高钛渣颗粒体积分数与高钛渣速度成反比关系，(如图4(a)、(b)和(d)、(e))；高钛渣沸腾氯化过程中，气泡上升过程中，气泡上部的高钛渣相不断从气泡两边向下运动，气泡上部的高钛渣在与气泡交互运动过程中获得了动能，当高钛渣向下运动到气泡尾部时，由于气泡尾涡的卷吸作用，少部分高钛渣被卷吸进入气泡相中，在气泡内部形成晕层与气泡一起上升；而无气泡处的高钛渣处于悬浮堆积状态，动能较小；因此，床层截面高钛渣速度图能够间接反应气泡相从高钛渣体积分数也能间接反应床层内部气泡行为，气泡相处，高钛渣颗粒从固相到气泡中心，体积分数逐渐减小，而高钛渣速度会逐渐增加，因此高钛渣速度增加的区间长度可以反应穿过该截面气泡直径大小；如图4(d)、(f)和图4(d)、(e)所示，床层截面的静压与颗粒体积分数呈正相关关系，从高钛渣颗粒聚集相→乳相→气泡相，静压力呈减小趋势，当达到气泡相处时静压最小，床层截面静压与床层截面的质量流量有关，高钛渣聚集相质量流量越大或者堆积密度较大，此时对气体阻碍作用明显，穿过床层的气流越少，床层静压越大。
根据上述分析，在沸腾氯化过程中，要求高钛渣相与氯气相分布相对均匀，因此可以将床层截面高钛渣颗粒速度大小和床层截面的压力作为评判依据。基于此，本文以1.5倍和1.6倍初始流化速度(
0.6375 m/s和0.68 m/s)值，在沸腾氯化时间为1.7 s时，导出床层截面为Y=0.1 m和Y=0.3 m处的速度分布和静压分布数据，并对速度分布和静压分布规律进行期望(E)计算和方差(D)计算，计算结果如表3所示。表 3 不同表观操作气速床层不同截面静压力分布和速度分布的期望与方差Table 3. The expectation and variance of static pressure distribution and velocity distribution in different sections of different superficial gas velocity表观操作气速/（m∙s-1） 床层位置/m 静压力分布 速度分布 期望(E) 方差(D) 期望(E) 方差(D) 0.6375 Y=0.1 − 1812.65 41.52 0.97 0.60 Y=0.3 − 4858.61 130.31 1.11 0.56 0.68 Y=0.1 − 1555.53 115.92 0.96 0.76 Y=0.3 − 4445.26 78.13 1.01 0.60 结合图4(a)和(d)床层截面Y=0.1 m处的最能体现床层内部高钛渣颗粒和氯气两相流的流动特征，而Y=0.3 m处，此时均处于气泡相破裂，高钛渣相和氯气相分布较为均匀。因此，本文以Y=0.1 m处的速度大小和压力大小为依据，确定最佳沸腾氯化速度；从表3可知，在表观操作气速为
0.6375 m/s时，床层截面速度大小方差为：41.52；而表观操作气速为0.68 m/s时，床层截面的速度分布的方差为：115.92，说明在表观操作气速为0.6 375 m/s时，床层速度波动范围或者速度大小波动剧烈程度小于表观操作气速为0.68 m/s时，此时，床层中高钛渣颗粒分布相对更均匀；因此从速度波动角度，确定高钛渣沸腾氯化表观操作气速应当选择0.6375 m/s；同理若以床层截面压力分布的方差为依据，确定高钛渣沸腾氯化表观操作气速为0.6375 m/s。因此，结合床层截面速度分布规律和压力分布规律，确定高钛渣沸腾氯化的最佳表观操作气速为1.5倍Grace公式计算的初始流化速度值。4. 结论
1）以高钛渣沸腾氯化为研究对象，采用初始流化速度经验计算公式结合欧拉双流模型，建立了高钛渣沸腾氯化的数学模型，对比高钛渣颗粒分布云图与B类颗粒流动特征，发现Grace初始流化速度计算公式得到初始流化速度值模拟结果符合B类颗粒的气固两相流特征。
2）基于数值计算得到的高钛渣颗粒云图分布规律，对比现有沸腾氯化气固两相流特征，综合考虑床层截面速度和压力分布规律，确定了高钛渣沸腾氯化的最佳表观操作气速应选择1.5倍Grace公式计算的初始流化速度值；
3）为了便于数值计算，采用单一粒径的钛渣为研究对象，通过数值计算得到钛渣沸腾氯化表观操作气速的选择依据，能够为实际生产过程中钛渣沸腾氯化表观操作气速的选择提供参考。
-
图 2 不同初始流化速度下高钛渣颗粒体积分数云图
（a-1）～（a-6）：初始流化速度为0.288 m/s (Ergun公式)；（b-1）～（b-6）：初始流化速度为0.319 m/s (Wen-Yu公式)；（c-1）～（c-6）：初始流化速度为0.425 m/s (Grace公式)
Figure 2. Particle volume fraction of high-titanium slag under different initial fluidization velocities
图 3 不同修正系数下固体颗粒体积分数云图
（a-1）～（a-6）: 1.1倍初始流化速度(0.4675 m/s)；（b-1）～（b-6）: 1.2倍初始流化速度(0.51 m/s)；（c-1）～（c-6）: 1.3倍初始流化速度(0.5525 m/s)；（d-1)～（d-6）: 1.4倍初始流化速度(0.595 m/s)；（e-1）～（e-6）: 1.5倍初始流化速度(0.6375 m/s)；（f-1）～（f-6）: 1.1倍初始流化速度(0.68 m/s)
Figure 3. Volume fraction of solid particles under different correction coefficients
图 4 不同表观操作气速下，高钛渣体积分数和不同截面处速度和压力的关系
(a)表观操作气速为0.6375 m/s，沸腾氯化时间为1.7 s时的高钛渣体积分数云图；(b)图(a)中Y=0.1 m 和Y=0.3 m处高钛渣颗粒速度；(c)图（a）中Y=0.1 m 和Y=0.3 m处床层截面静压；(d) 表观操作气速为0.68 m/s，沸腾氯化时间为1.7 s时的高钛渣体积分数云图；(e)图(d)中Y=0.1 m 和Y=0.3 m处高钛渣颗粒速度；(f) 图(d)中Y=0.1 m 和Y=0.3 m处床层截面静压
Figure 4. Relationship between the volume fraction of high titanium slag and the velocity and pressure at different sections under different apparent operating gas velocities
表 1 边界条件和模拟参数
Table 1. Boundary conditions and simulation model parameters
钛渣密度/(kg·m−3) 钛渣直径/m 初始体积分数 氯气密度/(kg·m−3) 初始静床高/m 床层空隙率 曳力模型 3810 5×10−4 0.7 2.95 0.24 0.61 Gidaspow 湍流模型 求解算法 内摩擦角/(°) 时间步长 时间步数 收敛标准 网格数目 RNG-k-ε Simple 30 10−4 30 000 0.0001 10 000 
下载: 导出CSV
表 2 不同经验公式计算的高钛渣初始流化速度
Table 2. Initial fluidization velocity of high titanium slag calculated by different empirical formulas
m/s 经验计算公式 Grace公式 Wen-Yu 公式 Ergun公式 计算值 0.425 0.319 0.288
下载: 导出CSV
表 3 不同表观操作气速床层不同截面静压力分布和速度分布的期望与方差
Table 3. The expectation and variance of static pressure distribution and velocity distribution in different sections of different superficial gas velocity
表观操作气速/（m∙s-1） 床层位置/m 静压力分布 速度分布 期望(E) 方差(D) 期望(E) 方差(D) 0.6375 Y=0.1 − 1812.65 41.52 0.97 0.60 Y=0.3 − 4858.61 130.31 1.11 0.56 0.68 Y=0.1 − 1555.53 115.92 0.96 0.76 Y=0.3 − 4445.26 78.13 1.01 0.60
下载: 导出CSV
-
[1] Bordbar Hossein, Ali Akbar Yousefi, Hossein Abedini. Production of titanium tetrachloride (TiCl4) from titanium ores: A review[J]. Polyolefins Journal, 2017,4(2):149-173. [2] Dai Yingjie, Wei Zhizhong, Wang Lijuan, et al. Study on impurity removal process of titanium tetrachloride produced by boiling chlorination[J]. Iron Steel Vanadium Titanium, 2022, 43(5): 40-44. (代应杰, 魏治中, 王丽娟, 等. 沸腾氯化生产四氯化钛除杂工艺探讨[J]. 钢铁钒钛, 2022, 43(05): 40-44.Dai Yingjie, Wei Zhizhong, Wang Lijuan, et al. Study on impurity removal process of titanium tetrachloride produced by boiling chlorination[J]. Iron Steel Vanadium Titanium, 2022, 43(5): 40-44. [3] Sun Kang. Titanium extraction metallurgy physical chemistry[M]. Beijing: Metallurgical Industry Press, 2001: 38-42. (孙康. 钛提取冶金物理化学 [M]. 北京: 冶金工业出版社, 2001: 38-42.Sun Kang. Titanium extraction metallurgy physical chemistry[M]. Beijing: Metallurgical Industry Press, 2001: 38-42. [4] Xiong Kun, Wen Shuming, Xie Meifang. Process mineralogy on titanium-rich slag in panzhihua[J]. Nonferrous Metals (Extractive Metallurgy), 2011(6):14-17. (熊堃, 文书明, 谢美芳. 攀枝花高钛渣的工艺矿物学[J]. 有色金属(冶炼部分), 2011(6):14-17.Xiong Kun, Wen Shuming, Xie Meifang. Process mineralogy on titanium-rich slag in panzhihua[J]. Nonferrous Metals (Extractive Metallurgy), 2011（6）: 14-17. [5] Guo Musun, Li Hongzhong. Review and prospect of fluidization science and technology[J]. Journal of Chemical Industry and Engineering, 2012,64(1):52-62. [6] Linghu Changhong. Application and discussion of high titanium sludge from Yunnan in fluidizing chlorination[J]. Light Metals, 2002(6):48-50. (令狐昌鸿. 云南高钛渣在沸腾氯化中的应用与探讨[J]. 轻金属, 2002(6):48-50. doi: 10.3969/j.issn.1002-1752.2002.06.014Linghu Changhong. Application and discussion of high titanium sludge from Yunnan in fluidizing chlorination[J]. Light Metals, 2002（6）: 48-50. doi: 10.3969/j.issn.1002-1752.2002.06.014 [7] Wang Jialin, Yang Yibang, Lu Yingwen, et al. The process control study on large scale boiling chlorinating furnace without screen plate[J]. Yunnan Metallurgy, 2017,46(4):77-80. (王佳林, 杨易邦, 陆应文, 等. 大型无筛板沸腾氯化炉工艺控制研究[J]. 云南冶金, 2017,46(4):77-80. doi: 10.3969/j.issn.1006-0308.2017.04.017Wang Jialin, Yang Yibang, Lu Yingwen, et al. The process control study on large scale boiling chlorinating furnace without screen plate[J]. Yunnan Metallurgy, 2017, 46（4）: 77-80. doi: 10.3969/j.issn.1006-0308.2017.04.017 [8] Kang Jungshin, Toru H Okabe. Thermodynamic consideration of the removal of iron from titanium ore by selective chlorination[J]. Metallurgical and Materials Transactions B, 2014,45:1260-1271. doi: 10.1007/s11663-014-0061-8 [9] Chen Yifan, Tang Xiaoning, Liu Shaopu, et al.Thermodynamic analysis of preparation of titanium tetrachloride by boiling chlorination process[J]. Nonferrous Metals Engineering, 2019, 9(5): 6-17. (陈一凡, 唐晓宁, 刘韶浦, 等. 沸腾氯化法制备四氯化钛过程热力学分析[J]. 有色金属工程, 2019, 9(5): 6-17.Chen Yifan, Tang Xiaoning, Liu Shaopu, et al.Thermodynamic analysis of preparation of titanium tetrachloride by boiling chlorination process[J]. Nonferrous Metals Engineering, 2019, 9(5): 6-17. [10] Tian Jian, Zhang Xiang, Huang Jiyu, et al. Technical analysis and comprehensive utilization of chlorinated waste during the production of TiCl4 by fluidized bed chlorination[J]. Titanium Industry Progress, 2018,35(3):6-11. (田键, 张祥, 黄季宇, 等. 沸腾氯化生产TiCl4工艺分析及氯化废料的综合利用[J]. 钛工业进展, 2018,35(3):6-11.Tian Jian, Zhang Xiang, Huang Jiyu, et al. Technical analysis and comprehensive utilization of chlorinated waste during the production of TiCl4 by fluidized bed chlorination[J]. Titanium Industry Progress, 2018, 35（3）: 6-11. [11] Ergun Sabri, Orning Ao Ao. Fluid flow through randomly packed columns and fluidized beds[J]. Industrial & Engineering Chemistry, 1949,41(6):1179-1184. [12] Wen C, Yu Y H. A generalized method for predicting the minimum fluidization velocity[J]. Aichc Journal, 1966,12(3):610-612. doi: 10.1002/aic.690120343 [13] Grace John R, Fariborz Taghipour. Verification and validation of CFD models and dynamic similarity for fluidized beds[J]. Powder Technology, 2004,139(2):99-110. doi: 10.1016/j.powtec.2003.10.006 [14] Mukesh Upadhyay, Ayeon Kim, Heehyang Kim, et al. An assessment of drag models in Eulerian–Eulerian CFD simulation of gas-solid flow hydrodynamics in circulating fluidized bed riser[J]. Chem Engineering, 2020,37(4):402-439. [15] Gidaspow Dimitri. Multiphase flow and fluidization: continuum and kinetic theory description[J]. Journal of Non-Newtonian Fluid Mechanics, 1994,55(2):207-208. doi: 10.1016/0377-0257(94)80007-3 [16] Jin Yong. Fluidization engineering principles[M]. Beijing: Tsinghua University Press, 2001. (金涌. 流态化工程原理[M]. 北京: 清华大学出版社, 2001.Jin Yong. Fluidization engineering principles[M]. Beijing: Tsinghua University Press, 2001. [17] Patil D J, Van S, Kuipers J. Critical comparison of hydrodynamic models for gas-solid fluidized beds-Part I: bubbling gas-solid fluidized beds operated with a jet[J]. Chemical Engineering Science, 2005,60(25):57-72. [18] Zhu Kuisong. Liu Songli, Gou Shuyun, et al. Numerical simulation for fluidized chlorination cold model of high-titanium slag in Yunnan[J]. Iron Steel Vanadium Titanium, 2017,38(2):30-36. (朱奎松, 刘松利, 芶淑云, 等. 云南高钛渣流态化氯化冷态模型数值模拟[J]. 钢铁钒钛, 2017,38(2):30-36. doi: 10.7513/j.issn.1004-7638.2017.02.005Zhu Kuisong. Liu Songli, Gou Shuyun, et al. Numerical simulation for fluidized chlorination cold model of high-titanium slag in Yunnan[J]. Iron Steel Vanadium Titanium, 2017, 38（2）: 30-36. doi: 10.7513/j.issn.1004-7638.2017.02.005 [19] El-Sadek M H, Fouad O A, Morsi M B, et al. Controlling conditions of fluidized bed chlorination of upgraded titania slag[J]. Transactions of the Indian Institute of Metals, 2019,72(2):423-427. doi: 10.1007/s12666-018-1493-7 -
下载:
点击查看大图
计量
- 文章访问数: 138
- HTML全文浏览量: 29
- PDF下载量: 13
- 被引次数: 0
